Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the Tracy–Singh product of two matrices
ResourceFunction["TracySinghProduct"][m1,m2,{r1,c1},{r2,c2}] gives the Tracy-Singh product of m1 and m2, where the ri and ci are corresponding integer partitions of the dimensions of the mi. |
The Tracy-Singh product of two partitioned matrices:
| In[1]:= | ![ResourceFunction["TracySinghProduct"][( {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
} ), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "4", "7"},
{"2", "5", "8"},
{"3", "6", "9"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), {{2, 1}, {2, 1}}, {{1, 2}, {1, 2}}] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/7c8/7c8ab69a-46b5-45ec-8276-885bbebebfec/3064ea297205cd72.png) |
| Out[1]= | 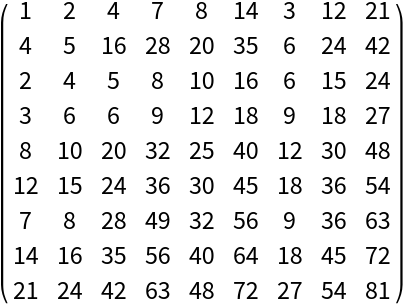 |
The Tracy-Singh product of two rectangular matrices with symbolic entries:
| In[2]:= |
| Out[2]= |  |
The Tracy-Singh product of two sparse matrices:
| In[3]:= | ![s = SparseArray[{i_, i_} :> i, {3, 3}];
t = SparseArray[{{i_, j_} /; Abs[i - j] == 1 :> i - j}, {4, 4}];
ResourceFunction[
"TracySinghProduct"][s, t, {{1, 2}, {2, 1}}, {{3, 1}, {2, 2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/7c8/7c8ab69a-46b5-45ec-8276-885bbebebfec/38e27ee87f07a278.png) |
| Out[3]= |
The Kronecker product is a special case of the Tracy-Singh product:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
The Tracy-Singh product is effectively the pairwise Kronecker product for each pair of partitions in the two matrices:

| In[6]:= | ![m1 = Array[\[FormalX], {5, 4}];
m2 = Array[\[FormalY], {2, 3}];
ResourceFunction["TracySinghProduct"][m1, m2, {{3, 2}, {2, 2}}, {{1, 1}, {1, 2}}] == tracySinghDef[m1, m2, {{3, 2}, {2, 2}}, {{1, 1}, {1, 2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/7c8/7c8ab69a-46b5-45ec-8276-885bbebebfec/053ecb71c02d918a.png) |
| Out[6]= |
This work is licensed under a Creative Commons Attribution 4.0 International License