Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test whether a graph is a partial order, that is, reflexive, antisymmetric and transitive
The graph representing the divisibility relation between integers is partial order since the relation is reflexive (each integer divides itself), antisymmetric (n cannot divide m if n>m) and transitive (as n|m implies m=kn for some integer k, so m|l implies n|l):
| In[1]:= |
| Out[1]= | 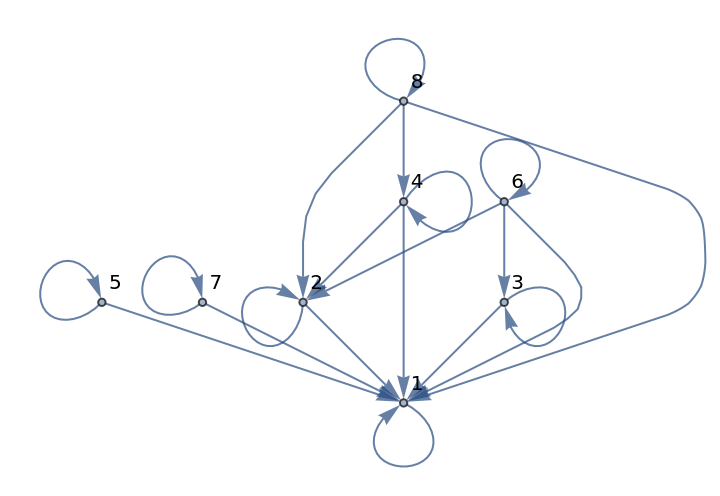 |
| In[2]:= |
| Out[2]= |
A graph formed by selecting ordered tuples is a partial order:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 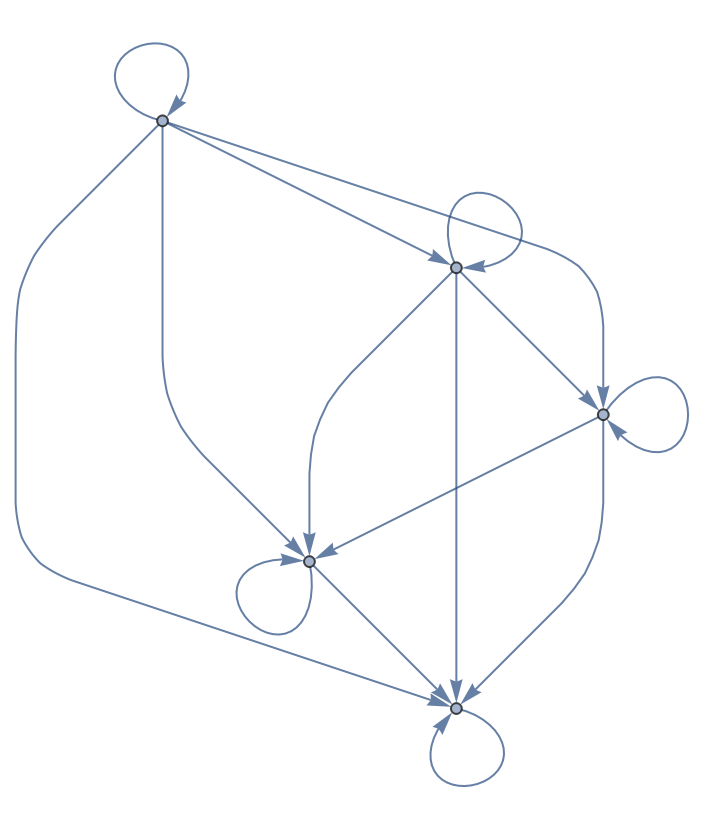 |
| In[5]:= |
| Out[5]= |
On the other hand, a similar graph constructed from the symmetric set of the tuples is not:
| In[6]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |
This work is licensed under a Creative Commons Attribution 4.0 International License