Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GenerateHexagonalWangTiling

Source Notebook

Generate a hexagonal tiling pattern from a set of hexagonal Wang tiles

Contributed by: Bowen Ping

ResourceFunction["GenerateHexagonalWangTiling"][tiles, init, n]

covers a n-layer hexagonal array with edge-matching Wang tiles, with init as the tile in the center.

Details

In the specification, init can be {} for no fixed tile.
Hexagonal Wang tiles are similar to square Wang tiles, except they have six edges rather than four.
Each element in tiles is a 6-element list, indicating the six colors numbered from southwest then counter clockwise: .
Option "Count" set the number of satisfiability instances. When "Count"→All is set, it gives all possible tilings.

Examples

Basic Examples (4) 

Generate a 1-layer hexagonal tiling with only one Hexagonal Wang tile:

In[1]:=
ResourceFunction[ "GenerateHexagonalWangTiling"][{{0, 1, 2, 0, 1, 2}}, {}, 2]
Out[1]=

Depict the tiling result:

In[2]:=
With[{tiles = {{0, 1, 2, 0, 1, 2}}, size = 2, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, Graphics[ depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]], ImageSize -> 200] ]
Out[2]=

Set the tile in the center:

In[3]:=
With[{tiles = {{0, 1, 2, 0, 1, 2}, {2, 0, 1, 2, 0, 1}, {1, 2, 0, 1, 2, 0}}, size = 2, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, Graphics[ depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][ tiles, {1, 2, 0, 1, 2, 0}, size]], ImageSize -> 200] ]
Out[3]=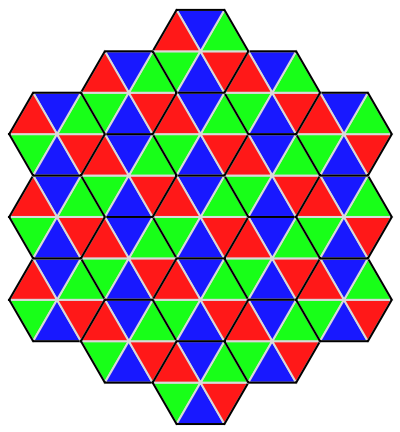

Make a bigger patch with 4-layer surroundings:

In[4]:=
With[{tiles = {{1, 0, 1, 1, 0, 1}}, size = 4, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, Graphics[ depictFunction[tiles, size, ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]], ImageSize -> 200] ]
Out[4]=

Scope (1) 

Generate aperiodic hexagonal Wang tiling:

In[5]:=
With[{tiles = CompressedData[" 1:eJw1j8ENAzEIBDEYG2xTRPpIFSnhGkj/v8Be7mGNLI3Y3df1/VxMRO98Ix81 ll5Q6fmfKgYw0Nj67bhJOb4EDsC2DI4b0fbZ0tlrtil0HnibRmd7a0ZhxOkA U0KIFSCdFmKkzcIza4/umbVP98o6fVXWGauy9lh5oPoAqw5Un7qTfepO9olQ dA5F52B0TlRn4O/kvHJyOxyAH3SK3F6dc3t1rtH6ANu1dimcvINdDOcGsmrX D9SMCUo= "], size = 10, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, With[{tiling = ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size]}, Labeled[ Graphics[depictFunction[tiles, size, tiling, ImageSize -> 800]] , Grid[ Partition[ Graphics[{#, {EdgeForm[Black], Opacity[0], Polygon[CirclePoints[{0, 0}, {2, \[Pi]}, 6]]}}, ImageSize -> 20] &@ MapThread[{Hue[#2], EdgeForm[LightGray], Polygon[{{0, 0}, Sequence @@ #1}]} &, {Partition[CirclePoints[{0, 0}, {2, \[Pi]}, 6], 2, 1, 1], #/(Max[tiles] + 1)}] & /@ tiles , 10]]] ]]
Out[5]=

Options (2) 

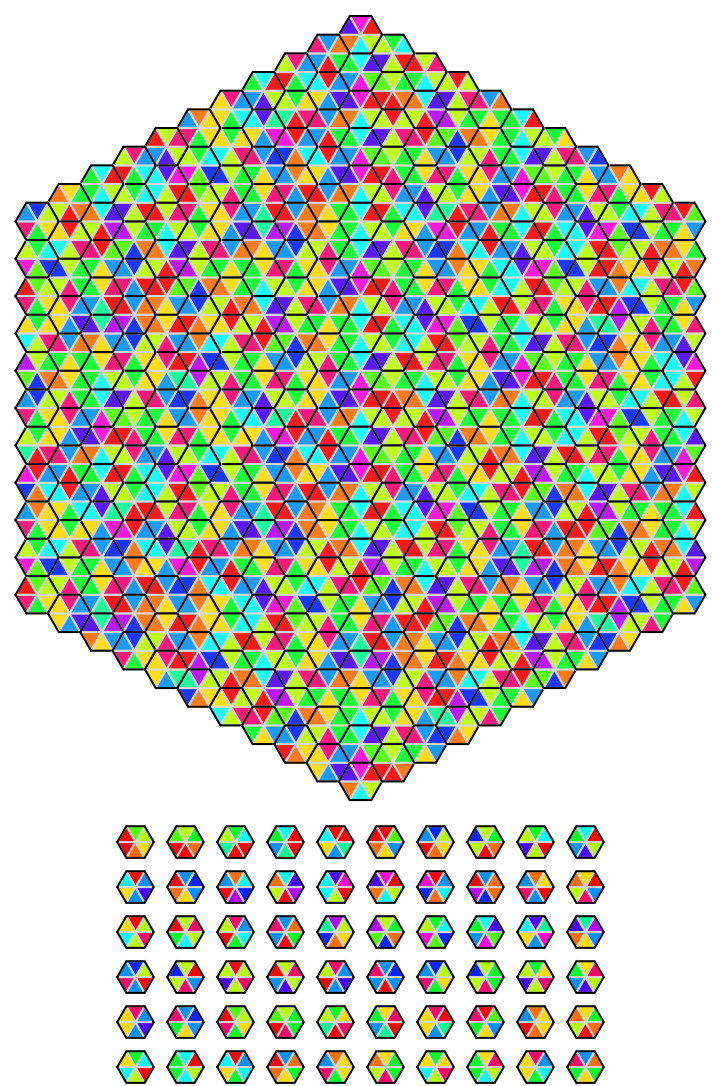Give two different possible tilings using "Count":

In[6]:=
With[{tiles = {{1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}, {1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}}, size = 3, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, Graphics[depictFunction[tiles, size, #, ImageSize -> 200]] & /@ ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size, "Count" -> 2] ] // List // Grid[#, Frame -> All, FrameStyle -> LightGray] &
Out[6]=

Give all possible tilings:

In[7]:=
With[{tiles = {{1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}, {1, 2, 0, 1, 2, 0}, {2, 0, 1, 2, 0, 1}, {0, 1, 2, 0, 1, 2}}, size = 3, depictFunction = Function[{tiles, size, result}, Map[With[{pos = Mean[ Catenate[ Part[#, All, 1]]]}, { MapApply[{ EdgeForm[LightGray], Opacity[0.9], #2, Polygon[{pos, Apply[Sequence, #]}]}& , #], { EdgeForm[ Directive[Black]], Opacity[0], Polygon[ CirclePoints[pos, {2, Pi}, 6]]}}]& , MapThread[# -> Hue[#2/(Max[tiles] + 1)]& , { Map[Partition[ CirclePoints[#, {2, Pi}, 6], 2, 1, 1]& , DeleteDuplicates[ Catenate[ NestList[DeleteDuplicates[ Catenate[ Map[CirclePoints[#, {2 Sqrt[3], 7 (Pi/6)}, 6]& , #]]]& , {{0, 0}}, size]]]], result}, 2]]]}, Graphics[depictFunction[tiles, size, #, ImageSize -> 200]] & /@ ResourceFunction["GenerateHexagonalWangTiling"][tiles, {}, size, "Count" -> All] ] // List // Grid[#, Frame -> All, FrameStyle -> LightGray] &
Out[7]=

Properties and Relations (1) 

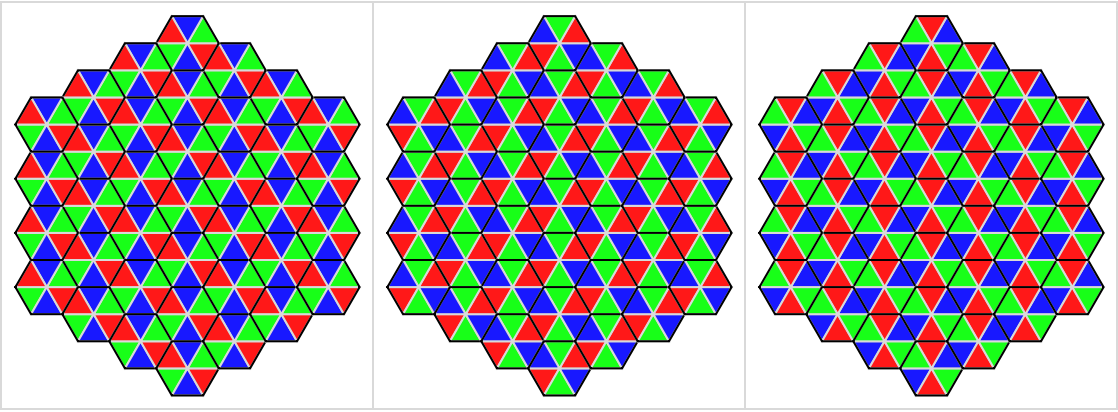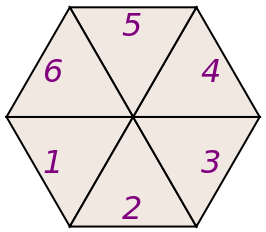
The number order in the 3-layer grid of the tiles is shown as following:

In[8]:=
With[{centerPoints = DeleteDuplicates[Catenate[ NestList[ DeleteDuplicates@ Catenate[ CirclePoints[#, {2 Sqrt[3], 7 Pi/6}, 6] & /@ #] &, {{0, 0}}, 3] ]]}, Graphics[ MapIndexed[{Opacity[1], EdgeForm[Black], White, Polygon[CirclePoints[#1, {2, Pi}, 6]], Black, Text[First[#2], #1]} &, centerPoints]] ]
Out[8]=

Neat Examples (1) 

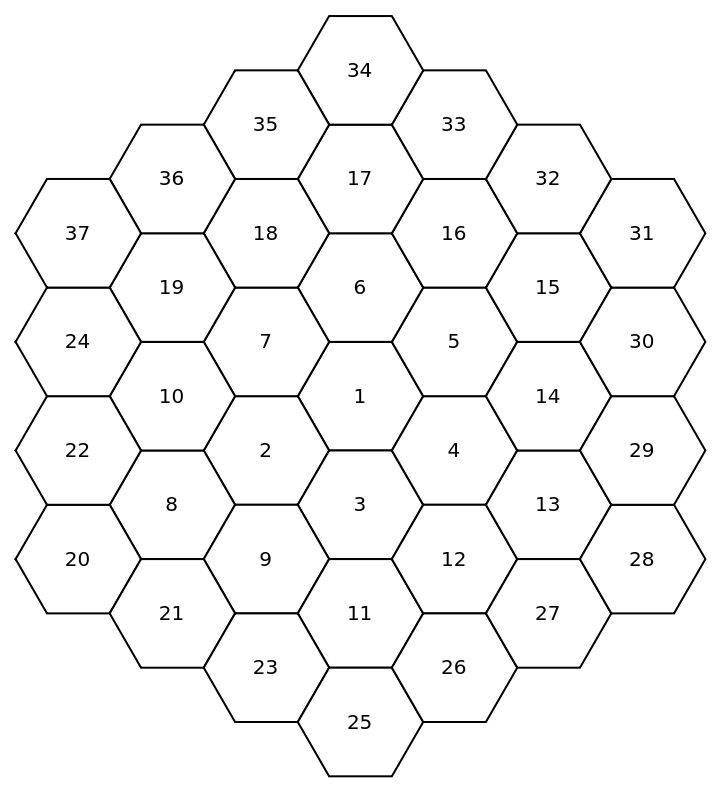Generate tilings of three different sets of aperiodic Hexagonal Wang tiles, all derived from the Hat tile:

In[9]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4c7093e6-3139-426d-ac10-b6f0c5d7c11f"]
Out[9]=

Publisher

Bowen Ping

Version History

  • 1.0.0 – 13 November 2023

Related Resources

License Information