Basic Examples (1) 

A 4×7 triangular grid graph:

In[1]:=

Out[1]=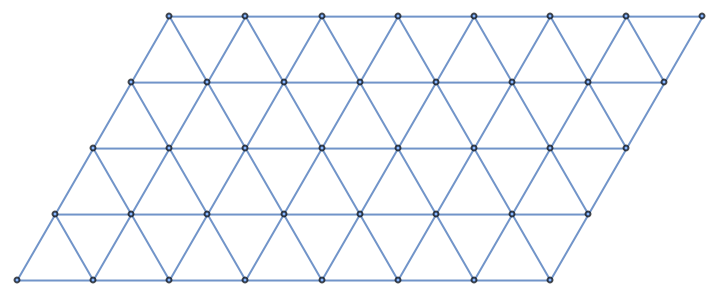

Scope (3) 

A triangular grid graph using only one argument:

In[2]:=

Out[2]=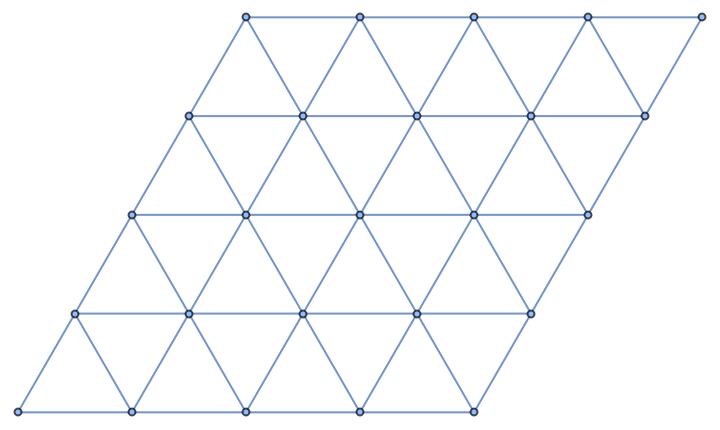

Use a non-default graph embedding:

In[3]:=

Out[3]=

Use a different plot theme:

In[4]:=

Out[4]=

Applications (1) 

Make a (full) triangular grid graph with vertices that are the centers of a hexagonal graph:

In[5]:=

Out[6]=

Properties and Relations (4) 

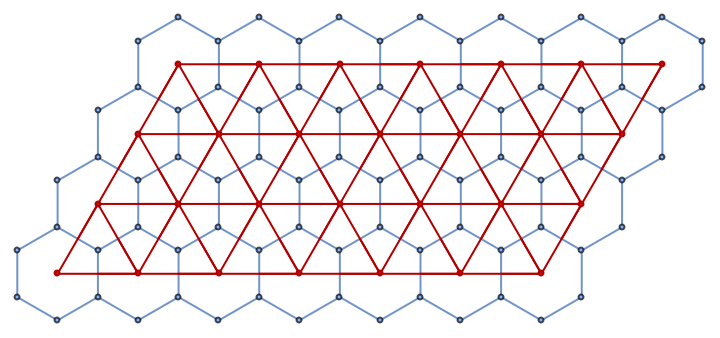The resource function "HexagonalGridGraph" takes width and height as arguments whereas TriangularLatticeGraph takes rows and columns, which is more consistent with GridGraph:

In[7]:=

Out[7]=

The resource function "TriangularGridGraph" takes only one argument for the graph size and makes triangle shaped graphs:

In[8]:=

Out[8]=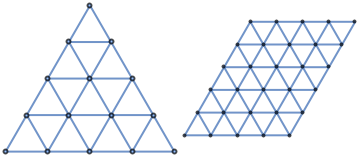

The mesh points of the Voronoi tessellation of the points of a triangular lattice graph contain the points of a hexagonal grid graph:

In[9]:=

Out[13]=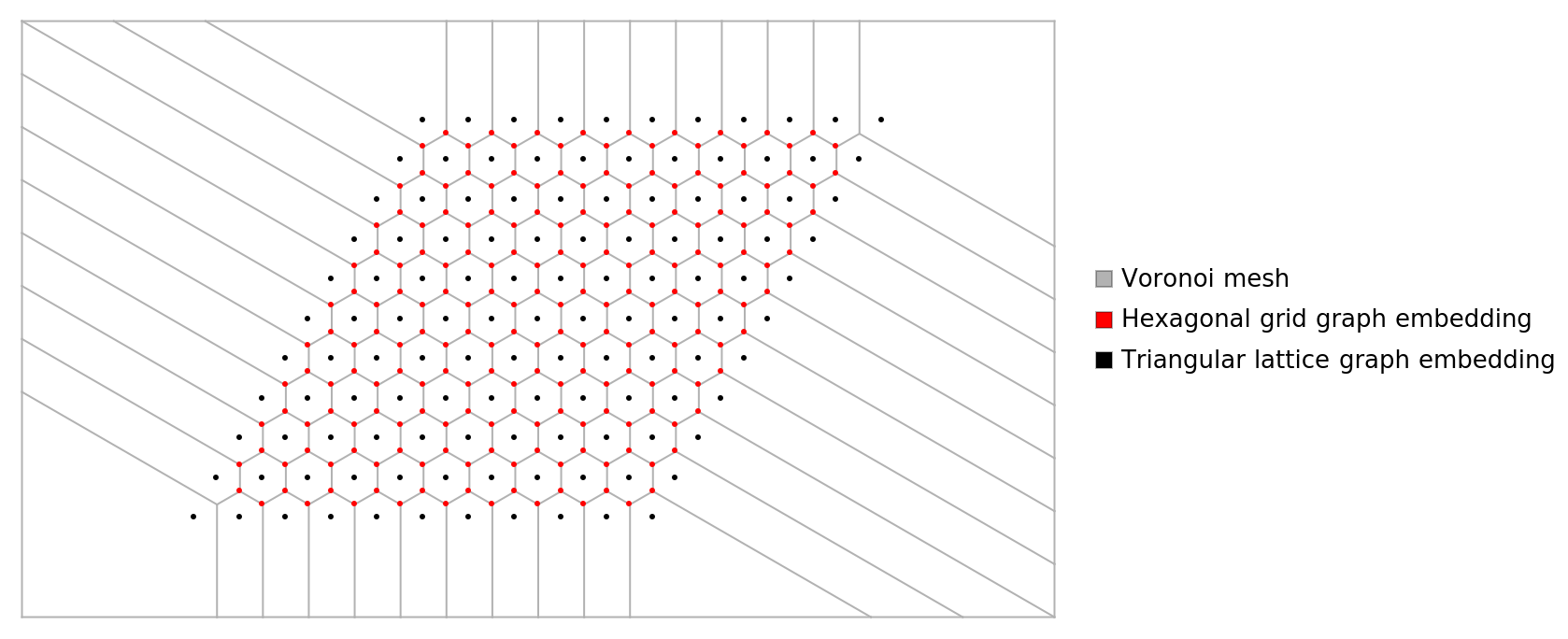

The opposite is also true:

In[14]:=

Out[14]=

Large graphs may be formatted differently in OutputForm than smaller ones; this 50×60 sample shows all edges:

In[15]:=

Out[15]=

In contrast, this 60×60 triangular grid graph displays as an elided Graph expression:

In[16]:=

Out[16]=