Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MeanDifferencePlot

Source Notebook

Plot the pairwise mean and difference between two data samples

Contributed by: Felipe Amorim

ResourceFunction["MeanDifferencePlot"][d1, d2]

plots the pairwise means against the differences of d1 and d2.

Details and Options

The mean difference plot, also known as the Bland–Altman plot, or Tukey mean-difference plot, compares two data samples by plotting the pairwise means (x-axis) and pairwise differences (y-axis) between two measurements.
The center line represents the mean of the differences, also called the bias. A value close to zero indicates good agreement between the two measurements. The upper and lower lines represent the limits of agreement, which, by default, represents the range where 95% of the differences are expected to lie. Points that fall outside of the limits may be considered outliers.
MeanDifferencePlot supports the same options of ListPlot, with the addition of the following:
"LimitOfAgreement"0.95value between 0 and 1 representing the range of the limits of agreement
The values for the mean and limit of agreement are displayed in the tooltips of each line.

Examples

Basic Examples (2) 

Create a mean difference plot between two data samples:

In[1]:=
ResourceFunction["MeanDifferencePlot"][{0, 1, 3}, {1, 3, 4}]
Out[1]=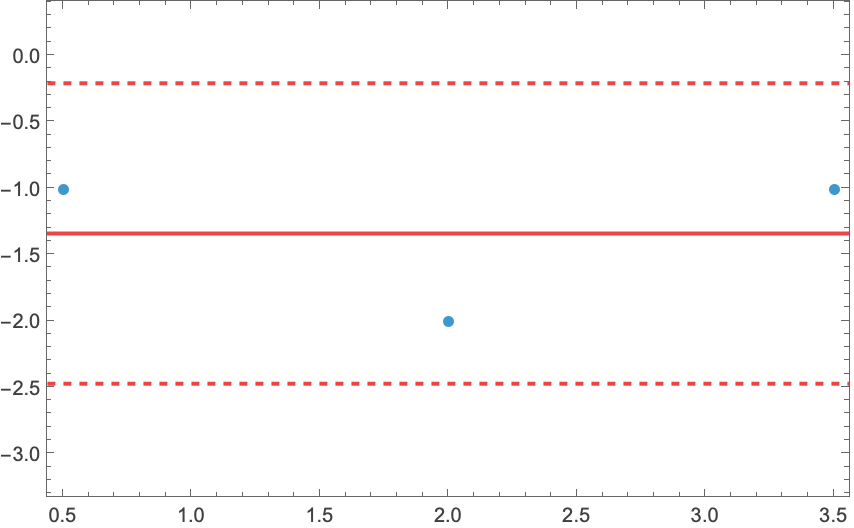

A more complex mean difference plot between two data samples:

In[2]:=
ResourceFunction[ "MeanDifferencePlot"][{-10, 3, 3, 1, -1, 2, 3, 9, 3}, {1, -4, 12, 3, 7, 5, 2, -2, -1}]
Out[2]=

Options (1) 

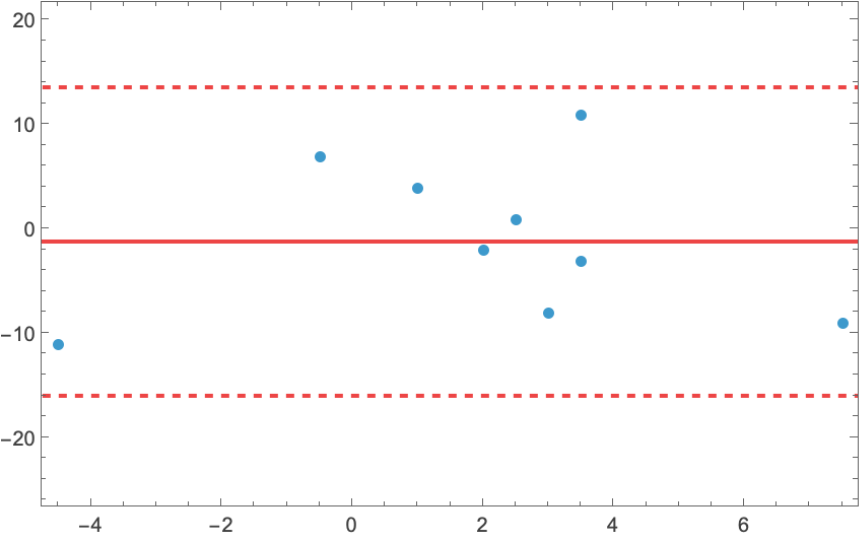Change the upper and lower limits of agreement with the "LimitOfAgreement" option:

In[3]:=
d1 = RandomReal[{-10, 10}, 100]; d2 = d1 + RandomReal[{1, 10}, 100]; GraphicsRow[ ResourceFunction["MeanDifferencePlot"][d1, d2, "LimitOfAgreement" -> #] & /@ {0.2, 0.6, 0.9}]
Out[5]=

Applications (2) 

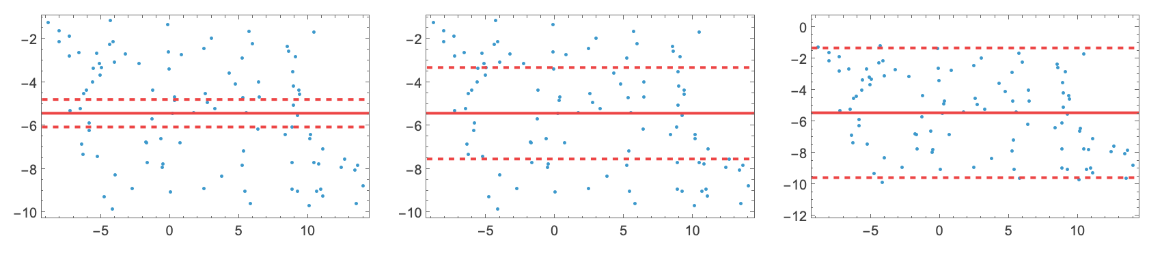Consider the case of two datasets containing glucose level readings for two different measurement methods:

In[6]:=
gluc1 = {82, 95, 101, 110, 118, 124, 130, 142, 155, 162, 170, 178, 185, 192, 205, 212, 225, 238, 250, 265}; gluc2 = {85, 97, 104, 108, 121, 127, 128, 145, 159, 160, 174, 181, 183, 196, 209, 215, 220, 242, 255, 270};

MeanDifferencePlot shows the agreement between readings of the two methods:

In[7]:=
ResourceFunction["MeanDifferencePlot"][gluc1, gluc2]
Out[7]=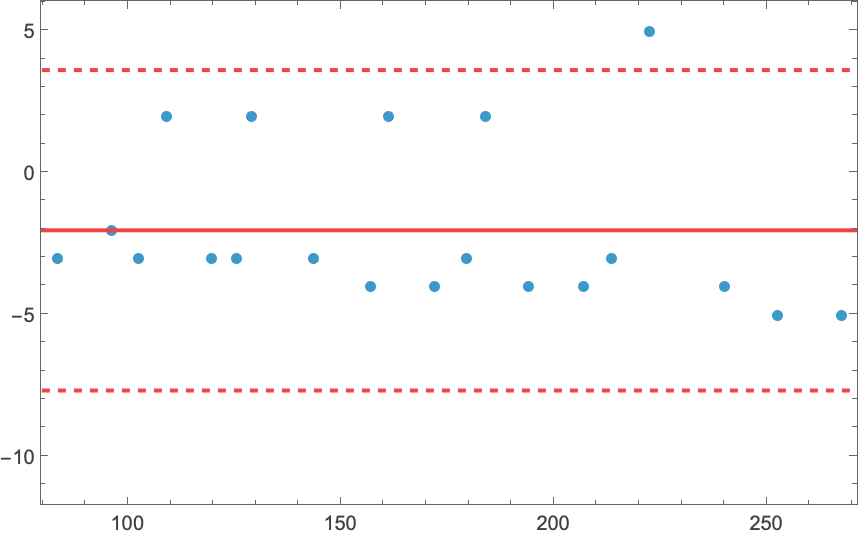

A negative bias shows that the second method reads lower glucose values that the first method on average.

Possible Issues (1) 

Data samples must have the same length:

In[8]:=
ResourceFunction["MeanDifferencePlot"][{-10, 3, 2}, {-4, 12}]
Out[8]=

Publisher

Felipe Amorim

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 08 December 2025

Related Resources

License Information