Basic Examples (3) 

Find the intersection of two circles:

In[1]:=

Out[1]=

The centers and radii can also be used:

In[2]:=

Out[2]=

Graphic of the circle and intersection points:

In[3]:=

Out[3]=

Scope (1) 

Use with inexact coordinates:

In[4]:=

Out[4]=

Applications (3) 

This function returns cleaner results when variables are used:

In[5]:=

Out[5]=

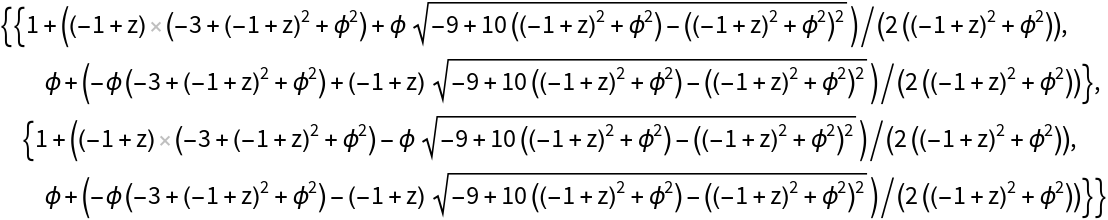
BooleanRegion remains unevaluated:

In[6]:=

Out[6]=

Here are two equivalent ways to use Solve:

In[7]:=

Out[7]=

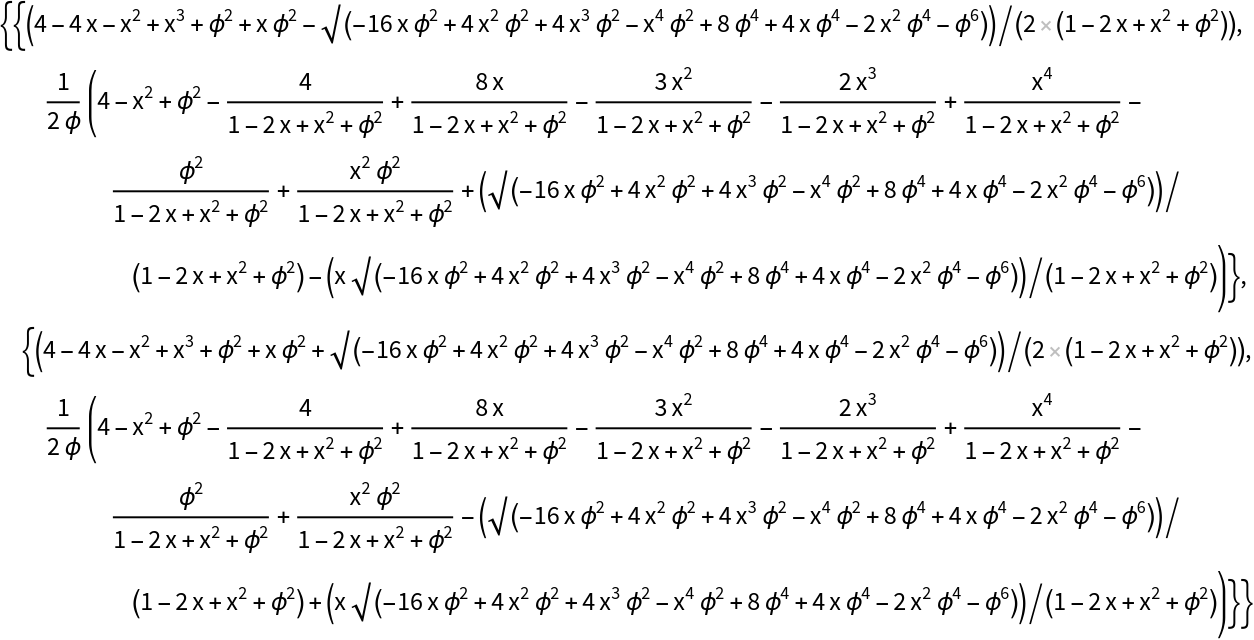
In[8]:=

Out[8]=

Properties and Relations (3) 

Find the intersection of two circles:

In[9]:=

Out[9]=

RegionIntersection gives the same answer:

In[10]:=

Out[10]=

BooleanRegion also gives the same answer:

In[11]:=

Out[11]=

Possible Issues (4) 

Some intersection points are nice:

In[12]:=

Out[12]=

More often the intersection points are messier:

In[13]:=

Out[13]=

When the distance between centers is equal to the sum of the radii (i.e. the two circles are mutually externally tangent), or if one circle is internally tangent to the other, the returned points will be identical:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

When the distance between centers exceeds the sum of the radii, or if one circle is completely inside the other, the returned points can be complex-valued:

In[16]:=

Out[16]=

In[17]:=

Out[17]=

When distance between points is zero (i.e. the circles are concentric), an empty list is returned:

In[18]:=

Out[18]=