Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BlockSubmatrices

Source Notebook

Decompose a matrix into a comprehensive set of smaller matrices

Contributed by: Bradley Klee

ResourceFunction["BlockSubmatrices"][data,{m,n}]

returns a List of associations that decompose data into a complete covering set of submatrices whose elements are partitioned into non-overlapping m×n blocks.

Details and Options

Each Association in the output list represents a block submatrix with the following keys and values:
"BlockData"elements of the block submatrix
"Offset"location of the submatrix within initial data
"MatrixDimensions"dimensions of initial data
"SubmatrixDimensions"flat dimensions of the submatrix
The entire list contains sufficient information for reconstructing the input matrix.
In a complete covering set, every possible m×n block appears in at least one block submatrix.
ResourceFunction["BlockSubmatrices"] takes the following options:
"Cyclic"{True,True}determines cyclic or terminal boundary conditions for row and columns
Method"MinimalCompletion"specifies how to achieve a complete cover of all possible m×n blocks
The choices for Method are as follows:
The "Atomize" method returns the exact covering of maximum cardinality where each block submatrix contains one unique block.
The "MinimalCompletion" method returns a most useful, tightly packed exact covering.
The "Lazy" method returns a covering with uniform submatrix dimensions, inexact with one or more cyclic boundary conditions.
The "Overkill" method is like the "Lazy" method, but returns more non-identical submatrices with one or more cyclic boundary conditions.

Examples

Basic Examples (3) 

List all 2×2 blocks of a multiplication table:

In[1]:=
ResourceFunction["BlockSubmatrices"][ Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}], {2, 2}]
Out[1]=

Check the exact covering property against "Atomize" method:

In[2]:=
Apply[SameQ, Sort[Flatten[#["BlockData"] & /@ ResourceFunction["BlockSubmatrices"][Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}], {2, 2}, Method -> #], 2] ] & /@ {"MinimalCompletion", "Atomize"}]
Out[2]=

Check completeness and inexactness of the "Lazy" method:

In[3]:=
Function[{filter}, Apply[SameQ, filter[ Flatten[#["BlockData"] & /@ ResourceFunction["BlockSubmatrices"][Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}], {2, 2}, Method -> #], 2] ] & /@ {"Lazy", "Atomize"}]] /@ {Union, Sort}
Out[3]=

Scope (2) 

Display a partitioning in graphical form:

In[4]:=
With[{data = Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}]}, ReplaceAll[Rule[pl[data], Grid[Partition[ MatrixForm[Map[pl, #["BlockData"], {2}] ] & /@ Flatten[Function[{dims}, Select[ResourceFunction["BlockSubmatrices"][data, {2, 2}], Dimensions[#["BlockData"]][[{1, 2}]] == dims &] ] /@ {{2, 2}, {2, 1}, {1, 2}, {1, 1}}, 1 ][[{1, 2, 5, 3, 4, 6, 7, 8, 9}]], 3], Frame -> All, Spacings -> {1, 1}, FrameStyle -> LightGray]], {pl[dat_] :> ArrayPlot[dat, PixelConstrained -> 32, ColorRules -> MapIndexed[(#2[[1]] - 1) -> Lighter[#1, .5] &, {Orange, Magenta, Green, Blue, Cyan}], Mesh -> True]}]]
Out[4]=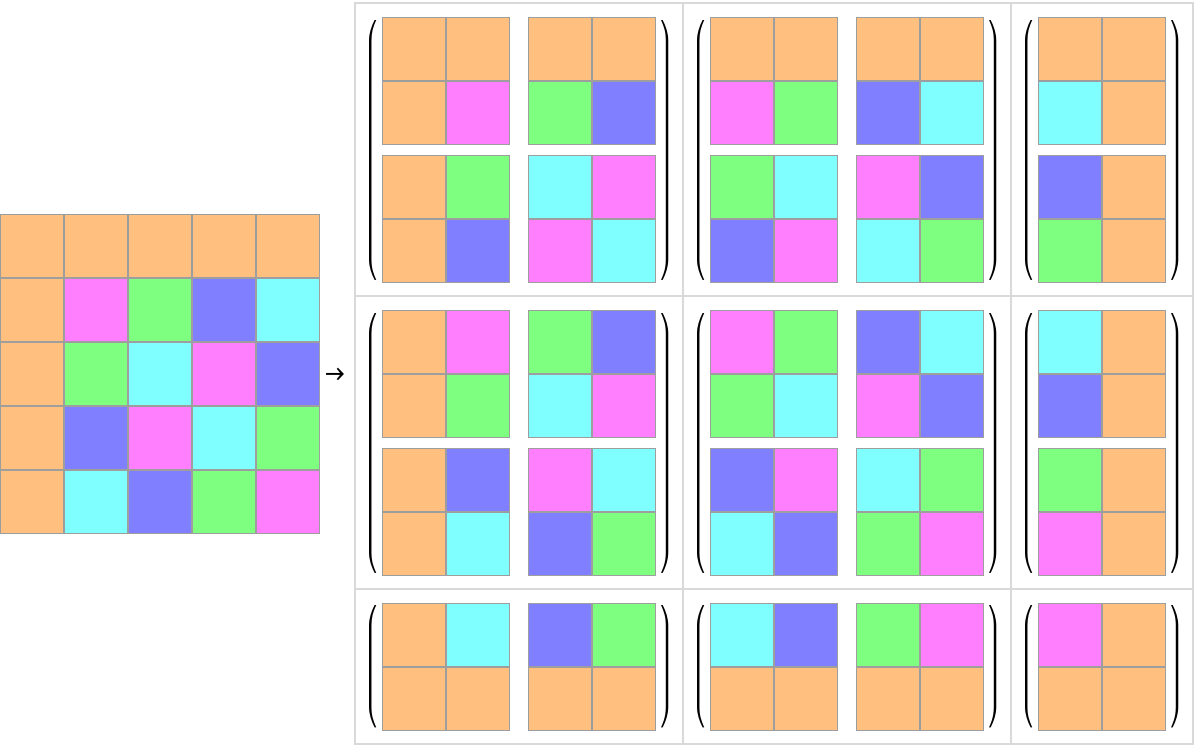

Compare with terminal (non-cyclic) boundary conditions:

In[5]:=
With[{data = Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}]}, ReplaceAll[Rule[pl[data], Grid[Partition[ MatrixForm[Map[pl, #["BlockData"], {2}] ] & /@ ResourceFunction["BlockSubmatrices"][data, {2, 2}, "Cyclic" -> {False, False}], 2], Frame -> All, Spacings -> {1, 1}, FrameStyle -> LightGray]], {pl[dat_] :> ArrayPlot[dat, PixelConstrained -> 32, ColorRules -> MapIndexed[(#2[[1]] - 1) -> Lighter[#1, .5] &, {Orange, Magenta, Green, Blue, Cyan}], Mesh -> True]}]]
Out[5]=

Properties and Relations (1) 

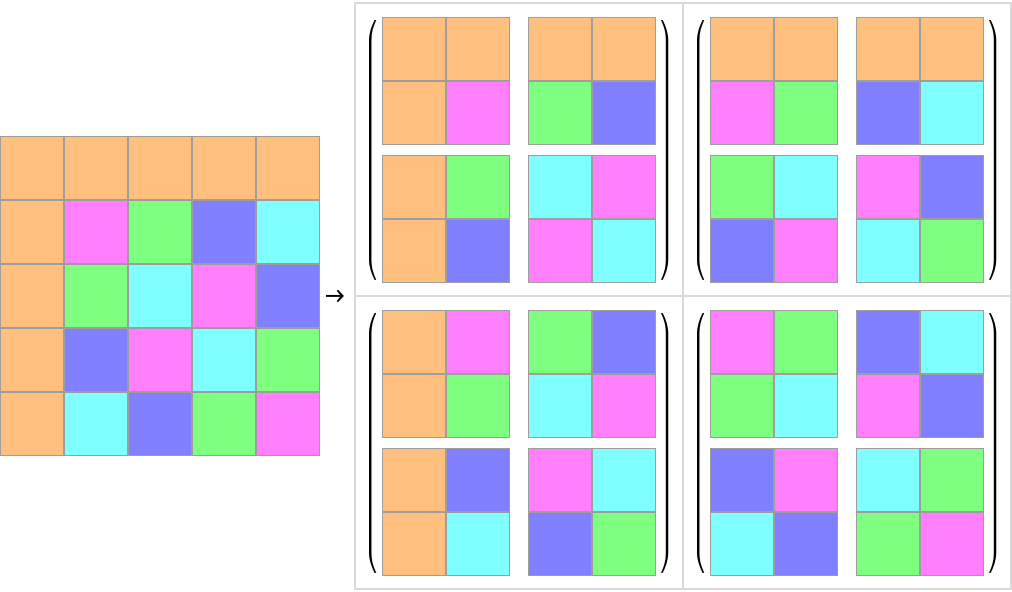It is possible to reconstruct input matrix from any output data set:

In[6]:=
SubmatrixMapping[blockSubmatrix_Association] := With[ {inds = Outer[List, Sequence @@ Mod[ Plus[blockSubmatrix["Offset"], Range /@ blockSubmatrix["SubmatrixDimensions"]], blockSubmatrix["MatrixDimensions"], 1], 1]}, MapThread[#1 -> #2 &, {inds, ArrayFlatten[blockSubmatrix["BlockData"]]}, 2]]
In[7]:=
RebuildTestSubmatrices[initMat_List, subMatData : {__Association}] := SameQ[ Subtract[initMat, Fold[ReplacePart, Times[0, initMat], Flatten[SubmatrixMapping[#]] & /@ subMatData]], Times[0, initMat]]
In[8]:=
With[{testInput = RandomInteger[5, {2*4*8, 2*4}]}, ArrayPlot[Transpose[testInput], ColorRules -> (# -> Hue[#/6] & /@ Range[0, 5]) ] -> RebuildTestSubmatrices[testInput, ResourceFunction["BlockSubmatrices"][testInput, RandomInteger[{1, 5}, 2], "Cyclic" -> RandomChoice[{True, False}, 2], Method -> RandomChoice[{"MinimalCompletion", "Lazy", "Overkill", "Atomize"}]]]]
Out[8]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 14 March 2022

Related Resources

License Information