Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the principal curvatures of a surface
ResourceFunction["PrincipalCurvatures"][s,{u,v}] computes the principal curvatures of the surface s with respect to variables u and v. | |
ResourceFunction["PrincipalCurvatures"][eq,{x,y,z}] computes the principal curvatures of the surface given by the implicit equation eq in variables x,y and z. |
Define a torus:
| In[1]:= |
|
| Out[1]= |
|
Calculate the principal curvatures:
| In[2]:= |
|
| Out[2]= |
|
The principal curvatures for an implicit surface:
| In[3]:= |
|
| Out[3]= |

|
Define the implicit Cartesian equation for the ellipsoid:
![]()
The principal curvatures:
| In[4]:= |
|
| Out[4]= |
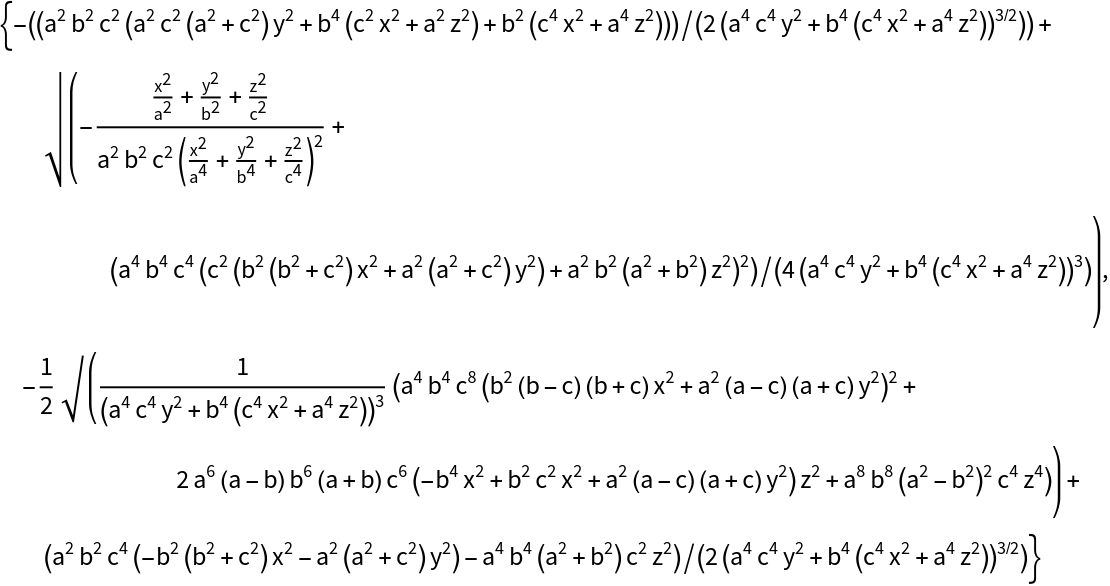
|
| In[5]:= |
|
| Out[5]= |
|
Define a surface:
| In[6]:= |
|
| Out[6]= |
|
Compute the Gaussian curvature and mean curvature:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
Principal curvatures are equal to ![]() :
:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
The principal curvatures are equal to the eigenvalues of the Weingarten matrix:
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
If the principal curvatures have the same sign everywhere, that means there are only elliptic points on the surface:
| In[14]:= |
![ResourceFunction["PrincipalCurvatures"][
Entity["Surface", "Sphere"]["ParametricEquations"][1][u, v], {u, v}] // PowerExpand](https://www.wolframcloud.com/obj/resourcesystem/images/6ed/6ed847f5-622c-4026-85ab-58cfe555230e/2349eb920738df09.png)
|
| Out[14]= |
|
Principal curvatures with different signs mean that there are only hyperbolic points on the surface:
| In[15]:= |
![FullSimplify[
PowerExpand[
ResourceFunction["PrincipalCurvatures"][
Entity["Surface", "HyperbolicParaboloid"]["ParametricEquations"][1,
1][u, v], {u, v}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/6ed/6ed847f5-622c-4026-85ab-58cfe555230e/1dc0120d5b7df64d.png)
|
| Out[15]= |
|
| In[16]:= |
|
| Out[16]= |
|
When at least one principal curvature is equal to zero everywhere, there are only parabolic points on the surface:
| In[17]:= |
![FullSimplify[
PowerExpand[
ResourceFunction[
"PrincipalCurvatures"][{Cos[u], Sin[u] + v, v}, {u, v}]], {u, v} \[Element] Reals]](https://www.wolframcloud.com/obj/resourcesystem/images/6ed/6ed847f5-622c-4026-85ab-58cfe555230e/18c01ed6fac3aad6.png)
|
| Out[17]= |
|
When both are equal to zero, there are only planar points on the surface:
| In[18]:= |
|
| Out[18]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License