Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return the Christoffel symbol for a given metric
ResourceFunction["ChristoffelSymbol"][metric,coords] creates the Christoffel symbol of the second kind for metric specified in coordinate variables coords. | |
ResourceFunction["ChristoffelSymbol"][metric,coords,"Kind"→"First"] creates the Christoffel symbol of the first kind. |
Christoffel symbol of the second kind for Euclidean cylindrical coordinates:
| In[1]:= | ![ResourceFunction["ChristoffelSymbol"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0"},
{"0",
SuperscriptBox["r", "2"], "0"},
{"0", "0", "1"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), {r, \[Phi], z}] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/6b5/6b5454f1-4ebf-42b7-b29f-018ea63228a6/398567dd4c0957bc.png) |
| Out[1]= | 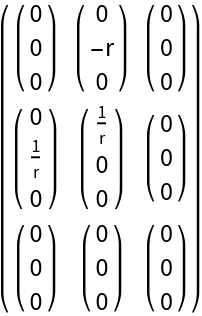 |
| In[2]:= |
| Out[2]= |
Christoffel symbol of the first kind for cylindrical coordinates:
| In[3]:= | ![ResourceFunction["ChristoffelSymbol"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0"},
{"0",
SuperscriptBox["r", "2"], "0"},
{"0", "0", "1"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), {r, \[Phi], z}, "Kind" -> "First"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/6b5/6b5454f1-4ebf-42b7-b29f-018ea63228a6/04d7e242fb64c4e8.png) |
| Out[4]= | 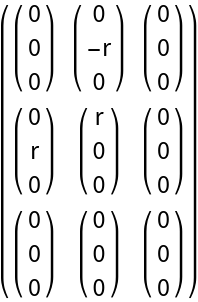 |
Christoffel symbols of a sphere:
| In[5]:= | ![ResourceFunction["ChristoffelSymbol"][
CoordinateChartData["Spherical", "Metric", {r, \[Theta], \[CurlyPhi]}],
{r, \[Theta], \[CurlyPhi]}, "Kind" -> "Second"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/6b5/6b5454f1-4ebf-42b7-b29f-018ea63228a6/106097ee10c97f45.png) |
| Out[6]= | 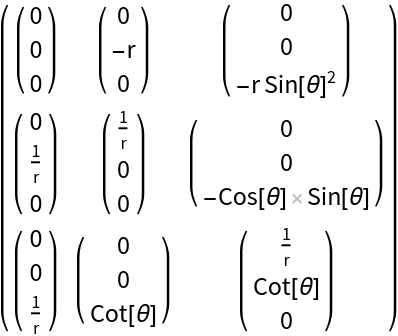 |
| In[7]:= | ![ResourceFunction["ChristoffelSymbol"][
CoordinateChartData["Spherical", "Metric", {r, \[Theta], \[CurlyPhi]}],
{r, \[Theta], \[CurlyPhi]}, Kind -> "First"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/6b5/6b5454f1-4ebf-42b7-b29f-018ea63228a6/58d615f92afda7fc.png) |
| Out[10]= | 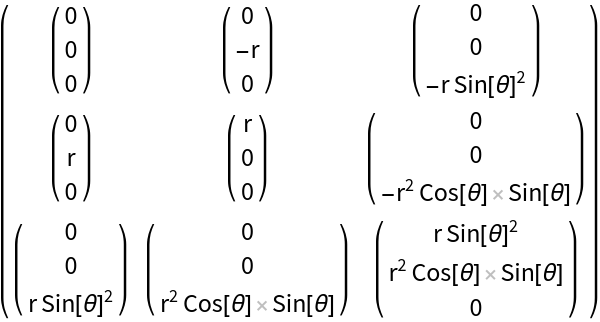 |
Describe a toroidal surface in ambient Cartesian space with surface coordinates:
| In[11]:= | ![x[\[Alpha]_, \[Beta]_] := (R + r Cos[\[Beta]]) Cos[\[Alpha]]
y[\[Alpha]_, \[Beta]_] := (R + r Cos[\[Beta]]) Sin[\[Alpha]]
z[\[Alpha]_, \[Beta]_] := r Sin[\[Beta]]](https://www.wolframcloud.com/obj/resourcesystem/images/6b5/6b5454f1-4ebf-42b7-b29f-018ea63228a6/50a4119be62bce8b.png) |
Plot the surface:
| In[12]:= |
| Out[12]= | 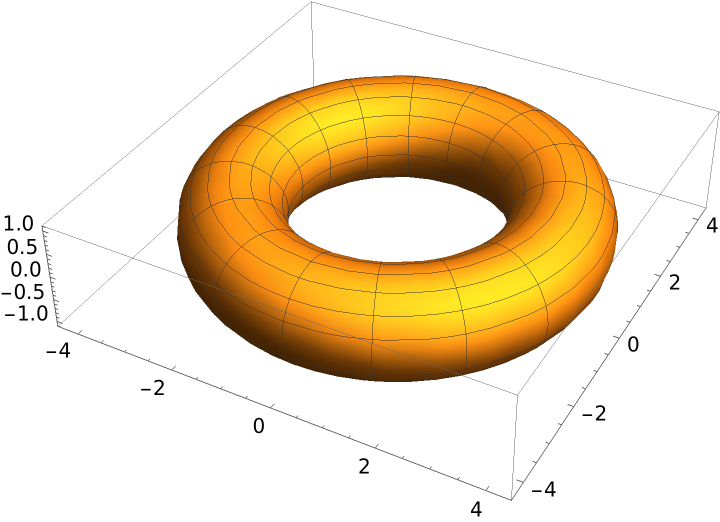 |
Form a covariant basis on the surface:
| In[13]:= |
| Out[13]= |
Get the covariant surface metric tensor:
| In[14]:= |
| Out[14]= |  |
This leads to the related Christoffel symbol of the second kind of the toroidal surface:
| In[15]:= |
| Out[17]= | 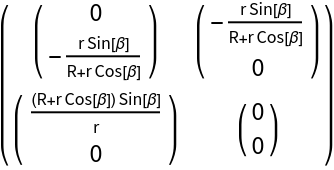 |
This work is licensed under a Creative Commons Attribution 4.0 International License