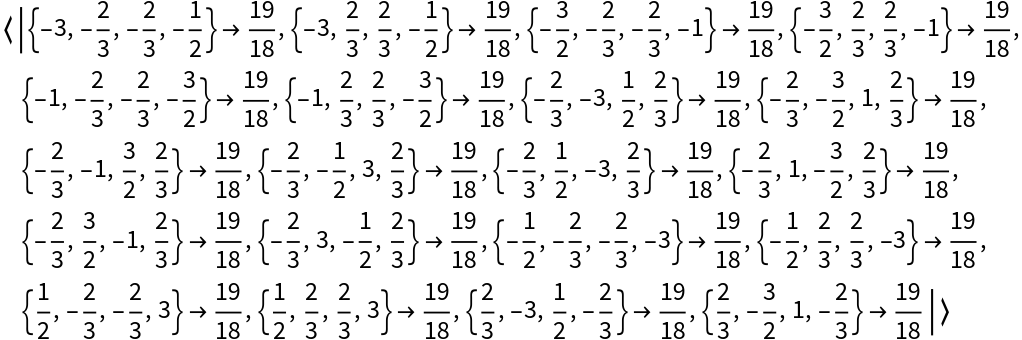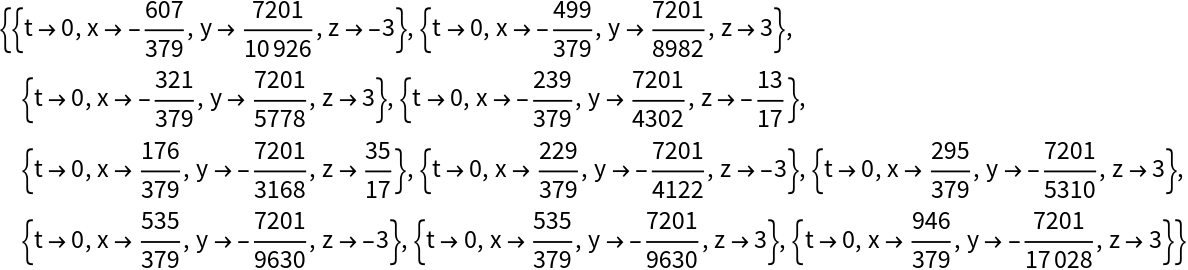Scope (6)
Get four results:
The results are all approximately equivalent:
Differing results of FindClosedForm can turn out to be strictly equivalent:
Get ten results based on Log:
The numerical match with the functional form is searched up to addition or multiplication by an algebraic number (that is, a Rational or Root):
The arguments can also be roots:
Specify the form of any function combination, with a number of arguments:
Search through a list of functional forms:
Options (36)
AlgebraicAdd (2)
Setting the option "AlgebraicAdd" to False allows one to search the specified functional form, up to multiplication (but not addition) by an algebraic number. This can vastly speed up the search, since special range properties are exploited for certain known functions:
Compare with the longer time required without this option:
AlgebraicFactor (2)
Setting the option "AlgebraicFactor" to False allows one to search the specified functional form, up to addition (but not multiplication) of an algebraic number:
Compare with the longer time required without this option:
If both "AlgebraicAdd" and "AlgebraicFactor" options are set to False, the search can be faster but may miss linear combinations of the functional form:
FormulaComplexity (2)
If not enough digits are specified, a careful balance between precision and complexity of the result should be reached through the option "FormulaComplexity". In fact, often the desired formula is likely to be the simplest. For example:
The result has the desired functional form and matches the digits:
However, by reducing the allowed complexity threshold, a simpler result is found:
By setting "FormulaComplexity" high, more intrinsically complex formulas can be found:
MaxSearchRounds (3)
The maximum number of argument search rounds is set to 50 by default. If the value of the option "SearchRange" is set to Automatic, this also means that the maximum integer argument and maximum rational argument denominator are both 50:
By default, larger or smaller arguments respectively are not reachable:
Changing the value for the option "MaxSearchRounds" allows a solution to be found:
MonitorSearch (2)
If the option "MonitorSearch" is set to True, the search round number is printed temporarily during evaluation:
If only one argument is specified, or a list of functions appears in the second argument, the function being evaluated is printed also:
OutputArguments (2)
If the option "OutputArguments" is set to True, the output is an association with the function arguments:
This option is especially useful in the case the functional form evaluates in such a way so to lose information on its arguments. For example, find a matrix whose determinant is equal to a certain number:
RationalSolutions (4)
By default, the option "RationalSolutions" is set to False. This means no simple rational solution is considered valid and more sophisticated solutions are searched for:
If the option "RationalSolutions" is set to True, a simpler exact solution can be found:
If the functional form searched for is the Identity, there is no need of this option:
Similarly when both the "AlgebraicFactor" and "AlgebraicAdd" options are set to false, rational solutions are automatically allowed:
The solution in this case is clearly:
RootApproximantMethod (4)
By default, only a limited set of algebraic numbers can be obtained (through a pre-defined lookup table):
It is possible to recognize other algebraic numbers by using the built-in function RootApproximant, through the option "RootApproximantMethod" set to "BuiltIn":
The problem with the built-in method is that most of the time is spent trying to recognize random reals as higher roots and this makes the search much slower. In this example, the search using the built-in method is over 100 times slower (and requires one more digit):
As an intermediate solution, in case some algebraic number is missed and you still want a fast search, you could specify a custom lookup table:
Notice that the built-in method may miss or misinterpret some algebraic numbers:
In case complex algebraic numbers are searched for, you can specify a custom table for their phases:
Without this option, the complex phase is assumed to be within π ResourceFunction["FareyRange"][-1,1,1/100]:
SearchArguments (2)
Through the option "SearchArguments" you can specify each particular search argument to be tried:
This can vastly speed up the search and serves as a debugging tool.
If more than one argument appears in the functional form, you can specify "SearchArguments" as a list of lists, or equivalently as an association:
SearchComplex (2)
Search for complex values of the argument:
Notice that this option determines only the complex character of the arguments, while complex values by themselves do not necessarily require it:
SearchQueries (2)
Return only the results from Wolfram Alpha by setting the option "SearchQueries" to 0:
If you specify a higher number, the number of results remains bounded by the second integer argument:
SearchRange (4)
By default, for each search round the arguments span the Farey range determined by ResourceFunction["FareyRange"][-round,round,round]. For example:
Otherwise, it is possible to set the option "SearchRange" to "Plain", which creates the shorter rational range Range[-round,round,1/round]:
Notice the longer time required with the default "Farey" range:
Of course, for other arguments, the converse may be true.
Another possible value for this option is "Integer", whereby only integer arguments are searched within the range Range[-round,round]:
It is possible to specify, as an option value, a custom range function of the search round number:
SearchTimeLimit (1)
Limit the time spent by the search algorithm:
Notice that, as in this example, the total time spent by the function may be higher than this option's value, because the time spent on querying Wolfram Alpha is not counted in it.
SignificantDigits (2)
The option "SignificantDigits" is automatically set to the number of real digits (before 0) specified in the given number. If you want to ignore some numerical error, you can specify a lower value for it:
Without this option setting, the same call takes a large amount of time:
The numerical error is less than the required precision:
Specify more significant digits than those available (consider extra digits as valid zeros):
The search is unsuccessful because the higher digits do not match:
Keep in mind that, with significant numerical error, the search for the right formula becomes much harder.
WolframAlphaQueries (2)
The number of Wolfram Alpha query results returned is, by default, 3:
You can either reduce or increase this number by setting the option "WolframAlphaQueries" to another number:
Notice that the queries may be unsuccessful, so this option just sets an upper limit:
Applications (4)
Besides finding formulae for raw numbers, FindClosedForm[y,f] can be used for verifying relations among special functions. For example, the following identity for EllipticK in terms of Gamma is not trivial to prove through symbolic computation:
However, FindClosedForm[y,f] can easily verify it:
Verify a formula for EllipticPi in terms of Gamma and Identity:
Find relations among different arguments of the same function through FindClosedForm[y,f,n]:
FindClosedForm[y,f,n] can be also used to find solutions to underdetermined systems of equations. For example, find instances of matrices whose determinant is equal to a certain number:
Compare with the solutions found through the built-in functions Reduce and FindInstance:
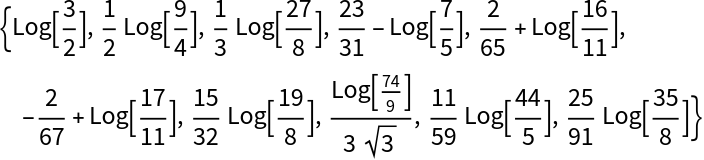
![ResourceFunction["FindClosedForm"][0.1013578, 1/(Gamma[#1] Gamma[#2]) &, "AlgebraicAdd" -> False] // AbsoluteTiming](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/232f79555721f9cc.png)
![ResourceFunction["FindClosedForm"][4.51766814, Gamma[#2]^3/Gamma[#1]^2 + Identity[#3] (Gamma[#1]^2/Gamma[#2]) &, "FormulaComplexity" -> 100]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/0aa9f6198d299cef.png)
![ResourceFunction["FindClosedForm"][19/18, Det[{{#1, #2}, {#3, #4}}] &,
"OutputArguments" -> True, "AlgebraicAdd" -> False, "AlgebraicFactor" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/413066a7bb57450d.png)
![ResourceFunction["FindClosedForm"][1.2596439236, Gamma, "FormulaComplexity" -> Infinity, "RootApproximantMethod" -> ResourceFunction["FareyRange"][0, 1, 2000]] // AbsoluteTiming](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/1c84e33597eb2997.png)
![TimeConstrained[
ResourceFunction["FindClosedForm"][1.2596439236, Gamma, "FormulaComplexity" -> Infinity, "RootApproximantMethod" -> "BuiltIn", "MonitorSearch" -> True] // AbsoluteTiming, 120]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/164f3c33a9b184e6.png)
![ResourceFunction["FindClosedForm"][7.38814 + 0.11606 I, Exp, "RootApproximantMethod" -> {Automatic, Range[-1, 1, 1/200]}]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/38d890f83b203cb3.png)
![EllipticK[2] == -((4 (-1)^(3/4) Gamma[5/4]^2)/Sqrt[\[Pi]]) // Map[N]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/1e57d709440ae819.png)
![EllipticK[2] == -((4 (-1)^(3/4) Gamma[5/4]^2)/
Sqrt[\[Pi]]) // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/0ba45b8817e90e22.png)
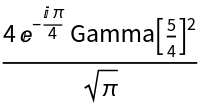
![ResourceFunction["FindClosedForm"][N[EllipticPi[1/2, 1/2]], Gamma[#2]^3/Gamma[#1]^2 + Identity[#3] (Gamma[#1]^2/Gamma[#2]) &, "AlgebraicAdd" -> False, "FormulaComplexity" -> 100]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/14080f7c669cabe3.png)
![EllipticPi[1/2, 1/2] == \[Pi]^(3/2)/(8 Gamma[5/4]^2) + (
4 Gamma[5/4]^2)/Sqrt[\[Pi]] // Map[N]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/07b5305146adaa5c.png)
![ResourceFunction["FindClosedForm"][
N[DedekindEta[1 + 2 I]], DedekindEta, 15, "SearchComplex" -> True, "FormulaComplexity" -> 100]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/0d2810e2c4802420.png)

![ResourceFunction["FindClosedForm"][19/18, Det[{{#1, #2}, {#3, #4}}] &, 20, "OutputArguments" -> True, "AlgebraicAdd" -> False, "AlgebraicFactor" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/688/6883506d-7b49-466e-b961-ea80307a98d8/52e5b1569dd06343.png)