Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Delannoy number
ResourceFunction["DelannoyD"][n,m] gives the Delannoy number D(n,m). |
Evaluate a Delannoy number:
| In[1]:= |
|
| Out[1]= |
|
DelannoyD threads elementwise over lists:
| In[2]:= |
|
| Out[2]= |
|
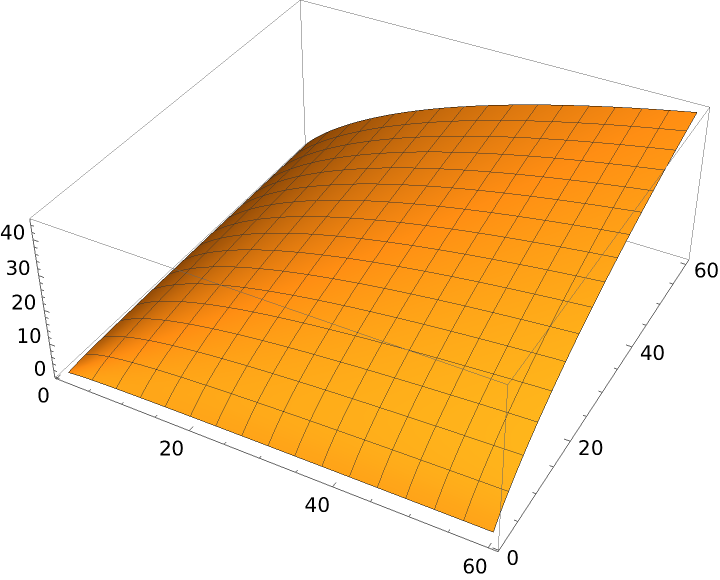
Plot Delannoy numbers on a logarithmic scale:
| In[3]:= |
|
| Out[3]= |
|
Find a formula for the central Delannoy numbers:
| In[4]:= |
|
| Out[4]= |
|
Generate values from the generating function:
| In[5]:= |
|
| Out[5]= |
|
| In[6]:= |
|
| Out[6]= |
|
Express the Delannoy number as a finite sum:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
Fractal-like pattern generated by a Delannoy number mod 7:
| In[9]:= |
![With[{m = 7}, ArrayPlot[
Mod[With[{d = 256}, Array[ResourceFunction["DelannoyD"], {d, d} + 1, {0, 0}]], m],
ColorFunction -> (Hue[#/10] &), ColorFunctionScaling -> False]]](https://www.wolframcloud.com/obj/resourcesystem/images/666/6662c350-77b6-467d-ae98-ae1027ad6f93/67cc298bca7e3a55.png)
|
| Out[9]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License