Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MolecularGraphAutocorrelation

Source Notebook

Compute molecular graph autocorrelation vectors, convolved over atomic properties

Contributed by: Joshua Schrier

ResourceFunction["MolecularGraphAutocorrelation"][mol]

returns the graph property autocorrelation function for the input Molecule mol.

ResourceFunction["MolecularGraphAutocorrelation"][str]

returns the graph property autocorrelation function for the input SMILES string str.

Details and Options

Standard autocorrelations (ACs) have the form where Pd is the AC for property P at depth d, δ is the Kronecker delta function and dij is the bond-wise path distance between atoms i and j. ACs of depth d encode relationships between properties of atoms separated by d bonds.
ResourceFunction["MolecularGraphAutocorrelation"] only supports a single molecular entity. It will fail for salts or for transition metal compounds.
The Wolfram Language’s covalent radii differ slightly from the ones used by MolSimplify.
ResourceFunction["MolecularGraphAutocorrelation"] supports the following options:
"Distance"3path length or distance between atoms
"PropertyKernels"(see below)properties to include in the computation
"OutputStyle""Vector"format of returned quantity
"PropertyKernels" can be any numeric AtomList property given by MoleculeValue["Properties"]["AtomProperties"]. The default properties, in order, are: "AtomicNumber", "Electronegativity", "CovalentRadius", "Identity", "CoordinationNumber".
"OutputStyle" options are "Vector", "Association" or "Matrix".

Examples

Basic Examples (2) 

The function can take either a SMILES string or a Molecule as input. By default, it returns a vector of 20 values, four values (0-, 1-, 2-, 3- neighbor autocorrelation distance) for each of the five default properties:

In[1]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O"]
Out[1]=

Redo using an explicit Molecule input form:

In[2]:=
ResourceFunction["MolecularGraphAutocorrelation"][ Molecule["Cn1c(=O)c2c(ncn2C)n(C)c1=O"]]
Out[2]=

Scope (2) 

Both the path length and the properties computed can be set as options. The returned vector has the dimension of the number of property kernels times the number of distances considered. In general, any AtomList property can be used in the "PropertyKernels" option value:

In[3]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "Distance" -> 0, "PropertyKernels" -> {"AtomicNumber"}]
Out[3]=

For small molecules without second- or third-nearest neighbors, the vector that is returned has zeros at those entries (for example, atoms in a water molecule are at most two bonds away from each other):

In[4]:=
ResourceFunction["MolecularGraphAutocorrelation"][Molecule["water"]]
Out[4]=

Changing the "OutputStyle" to "Association" clarifies that it is the fourth element (the third-neighbor) terms that are zero for each property:

In[5]:=
ResourceFunction["MolecularGraphAutocorrelation"][Molecule["water"], "OutputStyle" -> "Association"]
Out[5]=

Options (5) 

Distance (1) 

The option "Distance" controls the number of neighbors over which the graph correlation is calculated. The default value is 3 and must be a non-negative integer (0, 1, 2, 3, …):

In[6]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "Distance" -> 1]
Out[6]=

PropertyKernels (1) 

Use the "PropertyKernels" option to specify properties (from AtomList) to include in the calculations:

In[7]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "PropertyKernels" -> {"AtomicNumber"}]
Out[7]=

OutputStyle (3) 

Use the "OutputStyle" option to specify the format of returned quantity. The default is a "Vector" output:

In[8]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "OutputStyle" -> "Vector"]
Out[8]=

Other options include "Association", which returns an Association whose keys are the property and whose values are the vector of autocorrelated values for each distance:

In[9]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "OutputStyle" -> "Association"]
Out[9]=

The option "Matrix" returns a list of lists, arranged by property and then by distance:

In[10]:=
ResourceFunction[ "MolecularGraphAutocorrelation"]["Cn1c(=O)c2c(ncn2C)n(C)c1=O", "OutputStyle" -> "Matrix"]
Out[10]=

This "Matrix" setting for "OutputStyle" can be convenient for tabular data presentations:

In[11]:=
TableForm[%, TableHeadings -> { {"AtomicNumber", "Electronegativity", "CovalentRadius", "Identity", "CoordinationNumber"}, Range[0, 3]}]
Out[11]=

Neat Examples (1) 

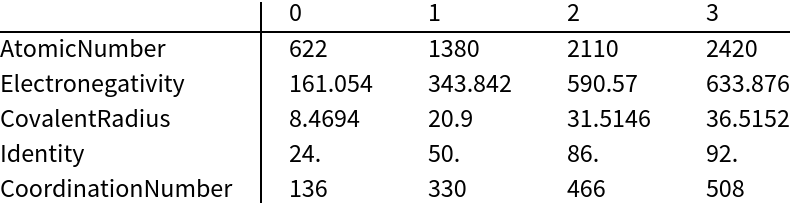Visualize molecular similarity by using the MolecularGraphAutocorrelation:

In[12]:=
(*Generate Molecule representations for a list of amines SMILES strings*) amines = Molecule /@ {"NCCN", "NCCCN", "NCCCCN", "NCCCCCN", "NCCCCCCCN", "NCCCNCCCCNCCCN", "CN(C)CCN(C)C", "CNCCNC", "C1CNCCN1", "CC1CNCCN1", "CC1CNC(C)CN1", "C1CN2CCN1CC2", "NC1CN2CCC1CC2", "NC1CCNC1", "NCC1CCCCN1", "CC1=NC=CN=C1"}; (*Compute the [\[FilledSmallSquare]] MolecularGraphAutocorrelation for the list*) gac = ResourceFunction["MolecularGraphAutocorrelation"] /@ amines; (*reduce the 20-dimensional autocorrelation vector down to 2 dimensions*) reduced = DimensionReduce[gac, Method -> "PrincipalComponentsAnalysis", FeatureExtractor -> "StandardizedVector"]; ListPlot[ (*visualization with mouseovers*) MapThread[Tooltip[#1, MoleculePlot[#2]] &, {reduced, amines}], AxesLabel -> {"PC1", "PC2"}]
Out[13]=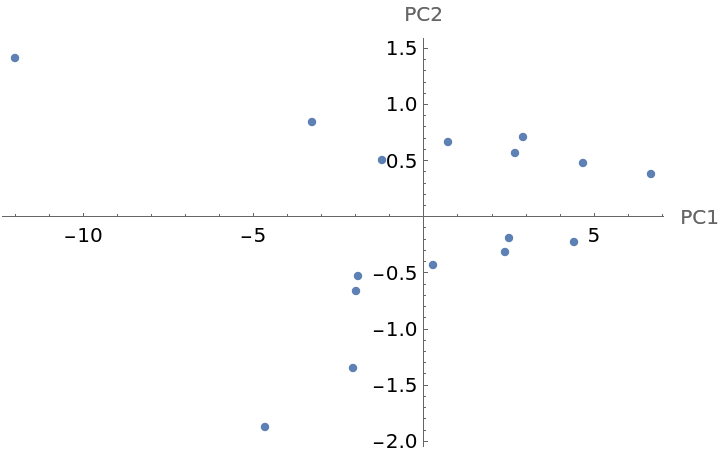

Each point in the graph has a Tooltip that shows the corresponding structure. In this example, the first principal component (PC1) is related to overall molecular size and the second principal component (PC2) captures whether the molecule has a ring (positive values) or not (negative values).

Publisher

Joshua Schrier

Version History

  • 1.0.0 – 16 December 2019

Source Metadata

  • Citation:
    • Moreau, G., Broto, P. "Autocorrelation of a topological structure: A new molecular descriptor." Nouv. J. Chim., vol. 4, 359–360, 1980.
    • Broto, P., Moreau, G., Vandycke, C., "Molecular structures: perception, autocorrelation descriptor and sar studies. system of atomic contributions for the calculation of the n-octanol/water partition coefficients." Eur. J. Med. Chem., vol. 19, no. 1, 71–78, 1984.
    • Virshup, A. M. et al., "Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-Like Compounds." J. Am. Chem. Soc., vol. 135, no. 19, 7296–7303, 2013. DOI: 10.1021/ja401184g
    • Janet, J. P. et al, "Leveraging Cheminformatics Strategies for Inorganic Discovery: Application to Redox Potential Design." Ind. Eng. Chem. Res., vol. 56, no. 17, 4898–4910, 2017. DOI: 10.1021/acs.iecr.7b00808
    • Janet, J. P., Kulik, H. J., "Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure–Property Relationships." J. Phys. Chem. A, vol. 121, no. 46, 8939–8954, 2017. DOI: 10.1021/acs.jpca.7b08750

License Information