Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test if a connected undirected graph is semi-Eulerian
Construct a graph with only two odd vertices:
| In[1]:= |
| Out[1]= | 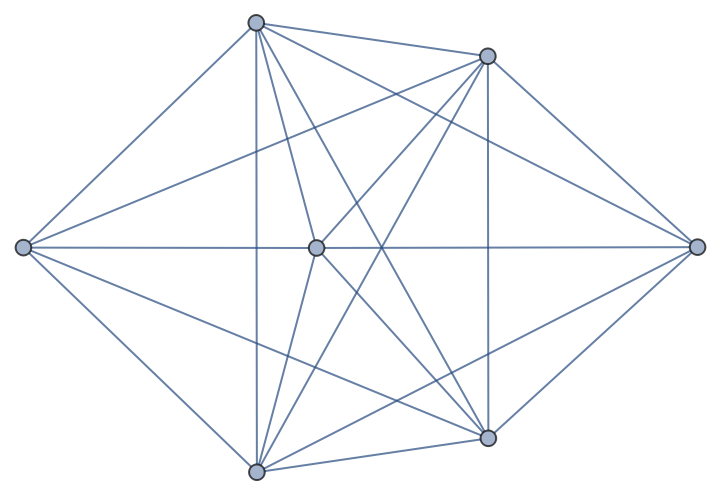 |
| In[2]:= |
| Out[2]= |
Test if the graph is semi-Eulerian:
| In[3]:= |
| Out[3]= |
Test if the graph is also Eulerian:
| In[4]:= |
| Out[4]= |
A graph with no odd vertices:
| In[5]:= |
| Out[5]= |  |
| In[6]:= |
| Out[6]= |
The graph is semi-Eulerian and Eulerian:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
A graph with more than two odd vertices:
| In[9]:= |
| Out[9]= | 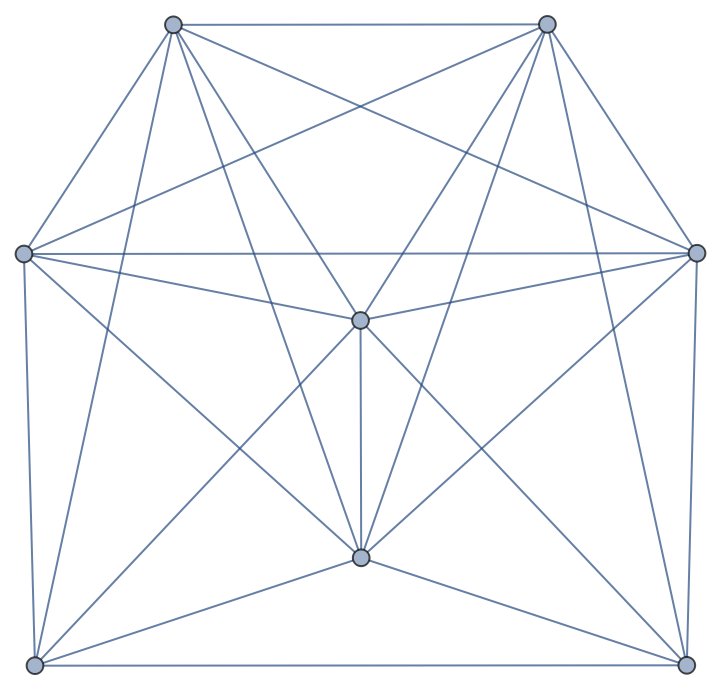 |
| In[10]:= |
| Out[10]= |
The graph is neither semi-Eulerian nor Eulerian:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
Test if a buckyball graph is semi-Eulerian:
| In[13]:= |
| Out[13]= |
Test if a torus graph is semi-Eulerian:
| In[14]:= |
| Out[14]= |
The multigraph representing the bridges of Königsberg is not semi-Eulerian:
| In[15]:= | ![bridgesOfKonigsberg = Graph[{\[ScriptCapitalA], \[ScriptCapitalB], \[ScriptCapitalC], \[ScriptCapitalD]}, {\[ScriptCapitalA] \[UndirectedEdge] \[ScriptCapitalB], \[ScriptCapitalA] \[UndirectedEdge] \[ScriptCapitalB], \[ScriptCapitalA] \[UndirectedEdge] \[ScriptCapitalC], \[ScriptCapitalA] \[UndirectedEdge] \[ScriptCapitalC], \[ScriptCapitalA] \[UndirectedEdge] \[ScriptCapitalD], \[ScriptCapitalB] \[UndirectedEdge] \[ScriptCapitalD], \[ScriptCapitalC] \[UndirectedEdge] \[ScriptCapitalD]}, VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/647/647e6ae5-e185-4098-abf7-36411e2c894b/13b7864e45416445.png) |
| Out[15]= | 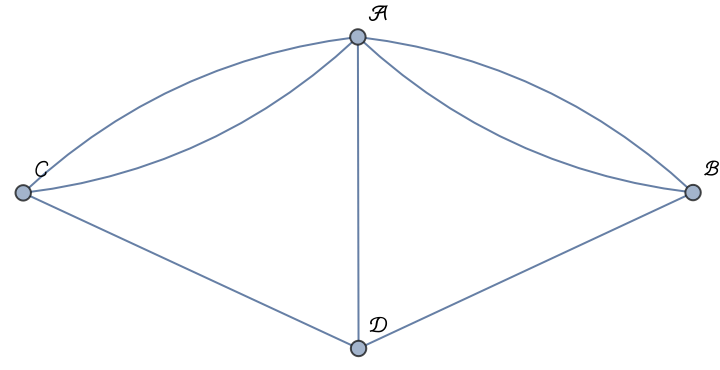 |
| In[16]:= |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License