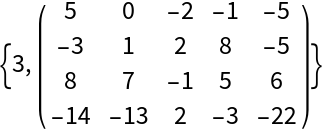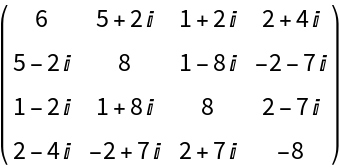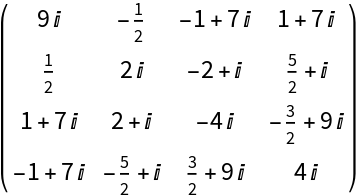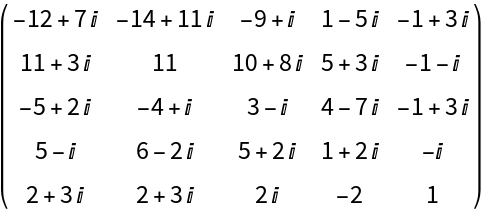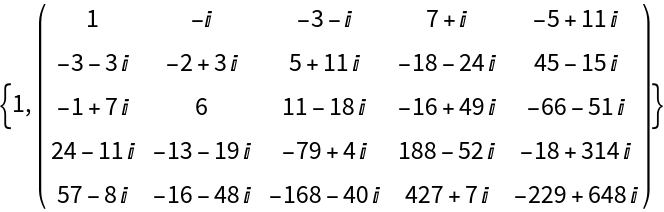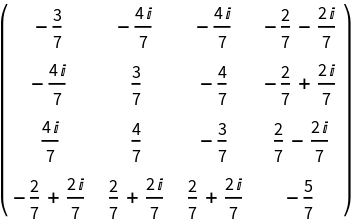Basic Examples (6)
A random 2×3 real matrix generated by real numbers between 0 and 1:
A random 4×5 integer matrix of rank 3 generated by integers between -5 and 10:
A random 4×4 rational matrix generated by integers between -5 and 10:
A random 4×5 Gaussian integer matrix of rank 3 generated by Gaussian integers between -5 and 10:
A random 4×5 matrix of rank 3 whose entries are Gaussian rationals generated by integers between -5 and 10:
A random 4×4 matrix of rank 2 whose entries are complex numbers generated by RandomComplex[{-5+2I,10-3I}]:
Scope (26)
Examples of special kinds of square matrices:
Triangular (1)
A random 4×4 upper triangular matrix with integer entries:
Symmetric (2)
A random 5×5 symmetric matrix with integer entries:
Check:
AntisymmetricMatrixQ or Skew-Symmetric (2)
A random 3×3 skew-symmetric matrix with integer entries:
Check:
A random 5×5 skew-symmetric matrix with rationals entries:
Check:
Hermitian (2)
A random 4×4 Hermitian matrix with Gaussian integer entries:
Check:
Skew-Hermitian (2)
A random 4×4 skew-Hermitian matrix with Gaussian integer entries:
Check:
A random 4×4 skew-Hermitian matrix with Gaussian rational entries:
Check:
Involution (2)
A random 4×4 involution matrix generated by vectors with integer entries and given range specifications:
Check:
Reflection (Symmetric Involution) (4)
A random 4×4 symmetric involution generated by vectors with integer and range specifications (geometrically these matrices represent orthogonal reflections in the column space of the matrix):
Check:
Verify that the column space is an invariant subspace:
Verify that vectors orthogonal to the column space are taken into their negatives:
Idempotent Symmetric (orthogonal projections) (2)
A random 4×4 Idempotent symmetric matrix generated by vectors with integer entries (geometrically these matrices represent orthogonal projections onto the column space of the matrix):
Check:
A random 6×6 idempotent symmetric matrix that represent the orthogonal projections onto a 4 dimensional subspace of the column space of the matrix):
Idempotent (2)
A random 5×5 idempotent matrix generated by vectors with integer entries:
Check:
A random 7×7 rank 5 idempotent matrix generated by vectors with integer entries:
Orthogonal (2)
A random 5×5 orthogonal matrix generated by vectors with integer entries:
Check:
Unimodular (Integer matrix with an integer inverse) (2)
A random 5×5 unimodular matrix with integer entries:
Check that the determinant is a unit and that the inverse has integer entries:
A random 5×5 unimodular matrix with Gaussian integer entries and a Gaussian integer inverse:
Check that the determinant is a unit and that the inverse has Gaussian integer entries:
Unitary (3)
A random 4×4 unitary matrix generated by vectors with Gaussian integer entries:
Check:
A random 4×4 unitary matrix with complex entries:
Check:
A random 4×4 unitary matrix with complex entries:
Check: