Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Given a 2D triangle and a point, get the specified data
ResourceFunction["TrianglePointData"][{a,b,c},p,property] Given triangle with coordinates {a,b,c} and point p, return property (see details). | |
Given triangle ABC and a point P (not on edge), then
| Trilinear | distance from P to triangle edges |
| Barycentric | (u,v,w) = areas (PBC,APC,ABP) normalized so that u+v+w=1 |
| InverseInCircum | Point X satisfies OX × OM = R2 where O is the circumcenter |
| Complement | |
| Anticomplement | |
| Isogonal | Reflect cevians by angle bisectors |
| Isotomic | Reflect cevians by midpoints |
| Cyclocevian | Draw circumcircle of cevian points, use other intersections |
| Antigonal | The isogonal conjugate of the inverse-in-circumcircle of the isogonal conjugate of P.("Pairs of Points: Antigonal, Isogonal, and Inverse," Mathematics Magazine 65 (1992) 339-347) |
| Synagonal | The antigonal image of the anticomplement of P. (following Hyacinthos #9881) |
| Cevian | The triangle made by the cevians |
| Anticevian | The triangle with ABC as the cevian triangle |
| Pedal | The triangle made by the altitudes |
| Antipedal | The triangle with ABC as the pedal triangle |
Given a triangle and point p, find the antipedal triangle:
| In[1]:= | ![tri = {{0, 1}, {0, -4}, {3, 0}};
p = {1, -1};
anti = ResourceFunction["TrianglePointData"][tri, p, "Antipedal"]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/7271ee564e9df834.png) |
| Out[3]= |
Edges perpendicular to lines from p to the triangle vertices give the antipedal triangle:
| In[4]:= |
| Out[4]= | 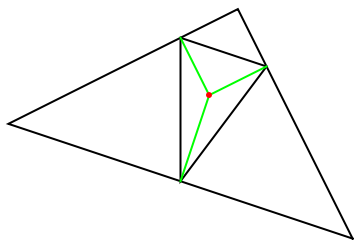 |
Show the trilinear:
| In[5]:= | ![delta = Triangle[{{-1, 1}, {4, 0}, {0, 3}}];
point = Point[{1, 1}];
object = ResourceFunction["TrianglePointData"][delta, point, "Trilinear"]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/525b4fabc701b337.png) |
| Out[7]= |
Show the barycentric:
| In[8]:= | ![delta = {{-1, 1}, {4, 0}, {0, 3}};
point = {1, 1};
object = ResourceFunction["TrianglePointData"][delta, point, "Barycentric"]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/7a79cfb6f3d48238.png) |
| Out[10]= |
Show a set of derived points:
| In[11]:= | ![delta = {{1.5, 2.5}, {-3.5, -2}, {3., -1.5}};
point = {1, 0};
objects = {#, ResourceFunction["TrianglePointData"][delta, point, #]} & /@ {"Complement", "Anticomplement", "Isogonal", "Isotomic", "Cyclocevian", "Antigonal", "Syngonal"};
Graphics[{EdgeForm[Black], White, Polygon[ delta], Green, Line[{point, #}] & /@ delta, Red, Point[{point}], {Black, #[[2]] & /@ objects, Text[#[[1]], #[[2, 1]], {-1.2, -1}] & /@ objects}}]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/5d0f849de266d2b1.png) |
| Out[12]= | 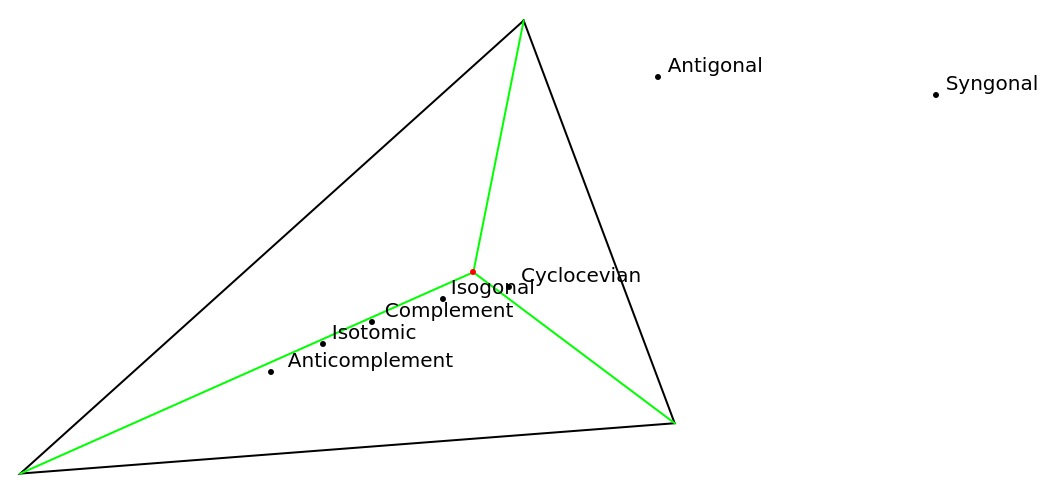 |
Show the cevian triangle:
| In[13]:= | ![delta = {{1.5, 2.5}, {-3.5, -2}, {3., -1.5}};
point = {1, 0};
object = ResourceFunction["TrianglePointData"][delta, point, "Cevian"];
Graphics[{EdgeForm[Black], White, Polygon[ delta], Green, Line[{point, #}] & /@ delta, Cyan, Point[{point}], {Opacity[0.5], EdgeForm[Black], object}}]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/45af1502984c4569.png) |
| Out[5]= | 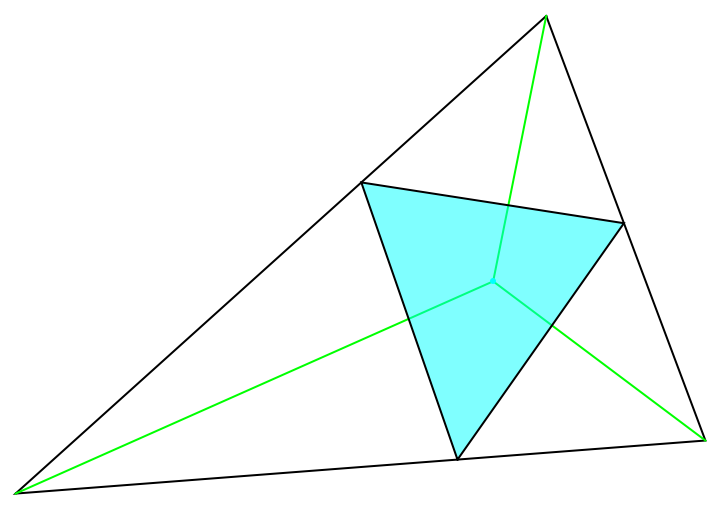 |
Show the anticevian triangle:
| In[14]:= | ![delta = {{1.5, 2.5}, {-3.5, -2}, {3., -1.5}};
point = {1, 0};
object = ResourceFunction["TrianglePointData"][delta, point, "Anticevian"];
Graphics[{EdgeForm[Black], White, Polygon[ delta], Green, Line[{point, #}] & /@ delta, Cyan, Point[{point}], {Opacity[0.1], EdgeForm[Black], object}}]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/73639c58dfe3874c.png) |
| Out[17]= | 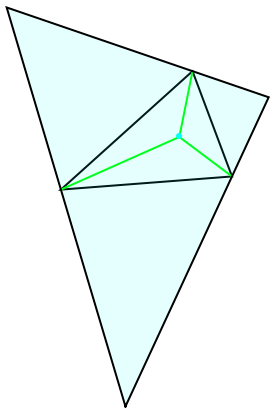 |
Show the pedal triangle:
| In[18]:= | ![delta = {{1.5, 2.5}, {-3.5, -2}, {3., -1.5}};
point = {1.5, 1};
object = ResourceFunction["TrianglePointData"][delta, point, "Pedal"];
Graphics[{EdgeForm[Black], White, Polygon[ delta], Green, Line[{point, #}] & /@ delta, Red, Point[{point}], {Opacity[0.1], EdgeForm[Black], object}}]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/228199d703e8b7a2.png) |
| Out[21]= | 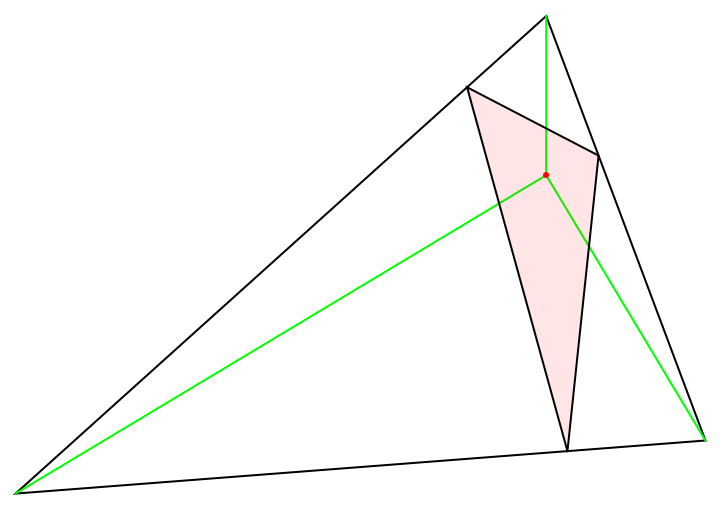 |
Construct the pedal triangle of a point:
| In[22]:= | ![Manipulate[
Module[{AA, BB, CC, MM}, AA = ptAA; BB = ptBB; CC = ptCC; MM = ptMM;
Graphics[{FontFamily -> Times, FontSize -> 14, PointSize[0.015],
{LightBlue, EdgeForm[{Thick, Blue}], Triangle[{AA, BB, CC}]}, {Opacity[0], EdgeForm[{Thin, Brown}], ResourceFunction["TrianglePointData"][{AA, BB, CC}, MM, "Pedal"]},
{Blue, Point[{AA, BB, CC}], Text["A", AA, {-1, -2}], Text["B", BB, {2, -1}], Text["C", CC, {2, 1}]}, {Red, Point[{MM}], Text["M", MM, {-1, 2}]}}, ImageSize -> {400, 230}, PlotRange -> {{-5.5, 5.5}, {-3.5, 3.5}}]],
{{ptAA, {1.5, 2.5}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None}, {{ptBB, {-3.5, -2}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None},
{{ptCC, {3., -1.5}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None}, {{ptMM, {-0.5, -0.75}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None}, SaveDefinitions -> True, TrackedSymbols :> {ptAA, ptBB, ptCC, ptMM}]](https://www.wolframcloud.com/obj/resourcesystem/images/5e7/5e732a5f-85cf-4d83-b573-745477d5b918/76b18310b1bb44ed.png) |
| Out[22]= | 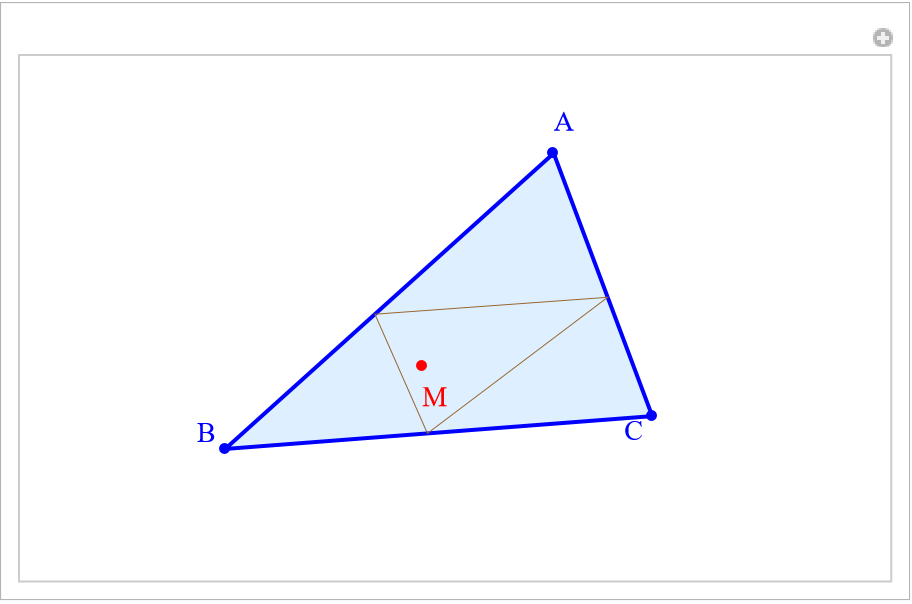 |
This work is licensed under a Creative Commons Attribution 4.0 International License