Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 KrawtchoukMatrix

Source Notebook

Generate a Krawtchouk matrix

Contributed by: Jan Mangaldan

ResourceFunction["KrawtchoukMatrix"][n]

returns an n×n Krawtchouk matrix.

Details and Options

The Krawtchouk matrix is also known as the binomial matrix.
The Krawtchouk matrix is a matrix with integer entries, whose entries are constructed from discrete orthogonal polynomials known as Krawtchouk polynomials.
The Krawtchouk matrix appears in algebraic coding theory, digital filters, multivariate splines, the Ehrenfest urn model and the modelling of Bernoulli random walks.
The Krawtchouk matrix, when multiplied with itself, gives a multiple of the identity matrix of the same size, where the multiple is 2n-1.
ResourceFunction["KrawtchoukMatrix"][…,"Normalized"→True] generates a normalized version of the Krawtchouk matrix such that the resulting matrix is both symmetric and orthogonal.
ResourceFunction["KrawtchoukMatrix"][…,WorkingPrecision→p] gives a matrix with entries of precision p.

Examples

Basic Examples (2) 

A 4×4 Krawtchouk matrix:

In[1]:=
ResourceFunction["KrawtchoukMatrix"][4]
Out[1]=

Visualize the entries of a Krawtchouk matrix:

In[2]:=
MatrixPlot[ResourceFunction["KrawtchoukMatrix"][20]]
Out[2]=

Options (5) 

Normalized (2) 

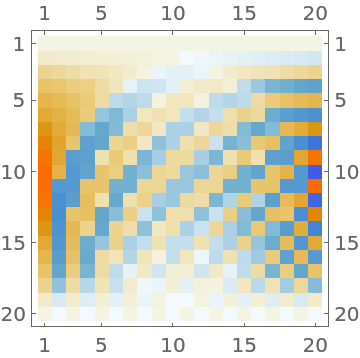A normalized Krawtchouk matrix:

In[3]:=
ResourceFunction["KrawtchoukMatrix"][6, "Normalized" -> True] // MatrixForm
Out[3]=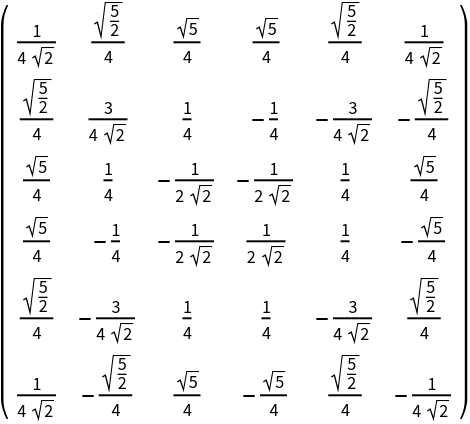

The normalized matrix is both symmetric and orthogonal:

In[4]:=
{SymmetricMatrixQ[%], OrthogonalMatrixQ[%]}
Out[4]=

WorkingPrecision (3) 

By default, an exact matrix is computed:

In[5]:=
ResourceFunction["KrawtchoukMatrix"][5] // MatrixForm
Out[5]=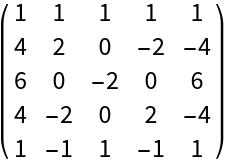

Use machine precision:

In[6]:=
ResourceFunction["KrawtchoukMatrix"][5, WorkingPrecision -> MachinePrecision] // MatrixForm
Out[6]=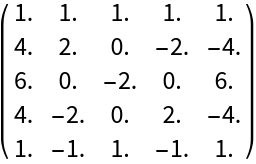

Use arbitrary precision:

In[7]:=
ResourceFunction["KrawtchoukMatrix"][5, WorkingPrecision -> 20] // MatrixForm
Out[7]=

Applications (6) 

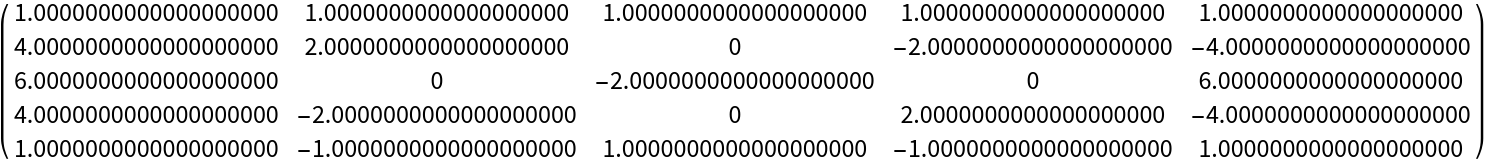Define a symmetrized version of the Krawtchouk matrix:

In[8]:=
symmetrizedKrawtchouk[n_] := ResourceFunction["KrawtchoukMatrix"][n] . DiagonalMatrix[Binomial[n - 1, Range[0, n - 1]]]

The symmetrized Krawtchouk matrix is symmetric, as its name implies:

In[9]:=
symmetrizedKrawtchouk[6] // MatrixForm
Out[9]=
In[10]:=
SymmetricMatrixQ[%]
Out[10]=

The symmetrized Krawtchouk matrix gives the coefficients of the bivariate polynomial (1+x+y-x y)n-1:

In[11]:=
With[{n = 7}, (1 + x + y - x y)^(n - 1) == symmetrizedKrawtchouk[n] . (x^Range[0, n - 1]) . (y^ Range[0, n - 1])] // Simplify
Out[11]=

Demonstrate a recursive method for generating the symmetrized Krawtchouk matrix:

In[12]:=
With[{n = 7}, BlockMap[Total[#, 2] &, ArrayPad[ KroneckerProduct[symmetrizedKrawtchouk[n], {{1, 1}, {1, -1}}], 1], {2, 2}] == symmetrizedKrawtchouk[n + 1]]
Out[12]=

The Kac matrix is a tridiagonal matrix whose subdiagonal and superdiagonal entries are consecutive integers:

In[13]:=
kac[n_] := With[{r = Range[n - 1]}, SparseArray[{Band[{2, 1}] -> r, Band[{1, 2}] -> Reverse[r]}, {n, n}]]
In[14]:=
kac[6] // MatrixForm
Out[14]=

The Kac matrix can be diagonalized by the symmetrized Krawtchouk matrix:

In[15]:=
symmetrizedKrawtchouk[6] . kac[6] . Inverse[symmetrizedKrawtchouk[6]] // MatrixForm
Out[15]=

Properties and Relations (4) 

Columns of the Krawtchouk matrix can be determined from the coefficients of the polynomial (1+x)n-j-1(1-x)j:

In[16]:=
With[{n = 5}, Transpose[ Table[CoefficientList[(1 + x)^(n - j - 1) (1 - x)^j, x], {j, 0, n - 1}]]]
Out[16]=
In[17]:=
% == ResourceFunction["KrawtchoukMatrix"][5]
Out[17]=

The entries of the Krawtchouk matrix can be expressed in terms of the Krawtchouk polynomial, which can be expressed in terms of Hypergeometric2F1:

In[18]:=
With[{n = 5}, Table[Binomial[n - 1, j - 1] Hypergeometric2F1[1 - j, 1 - k, 1 - n, 2], {j, n}, {k, n}]]
Out[18]=
In[19]:=
% == ResourceFunction["KrawtchoukMatrix"][5]
Out[19]=

Generate the Krawtchouk matrix through a recursive definition:

In[20]:=
With[{n = 5}, Array[Which[#1 == 0, 1, #2 == 0, Binomial[n - 1, #1], True, #0[#1, #2 - 1] - #0[#1 - 1, #2] - #0[#1 - 1, #2 - 1]] &, {n, n}, {0, 0}]]
Out[20]=
In[21]:=
% == ResourceFunction["KrawtchoukMatrix"][5]
Out[21]=

The product of a Krawtchouk matrix with itself is a constant multiple of the identity matrix of the same size:

In[22]:=
Table[With[{km = ResourceFunction["KrawtchoukMatrix"][n]}, km . km == 2^(n - 1) IdentityMatrix[n]], {n, 2, 9}]
Out[22]=

Neat Examples (2) 

Generate a Krawtchouk matrix from a Hadamard matrix, using condensation of the rows and columns with the same binary weights (number of 1's in the binary representation):

In[23]:=
n = 7; hm = 2^((n - 1)/2) HadamardMatrix[2^(n - 1), Method -> "BitComplement"]; idx = Values[ KeySort[GroupBy[ Table[{k, DigitCount[k, 2, 1]}, {k, 0, 2^(n - 1) - 1}], Last -> First]]] + 1; km = Table[Total[hm[[ji, ki]], 2], {ji, idx}, {ki, idx}] . DiagonalMatrix[1/Binomial[n - 1, Range[0, n - 1]]]
Out[24]=

Verify that the result is a Krawtchouk matrix:

In[25]:=
km == ResourceFunction["KrawtchoukMatrix"][n]
Out[25]=

Version History

  • 1.0.0 – 01 March 2023

Source Metadata

  • Citation:
    • Boyd G., Micchelli C.A., Strang G., Zhou D.X., "Binomial Matrices." Advances in Computational Mathematics, vol. 14, no. 4, 379-391, 2001.
      DOI: 10.1023/A:1012207124894
    • Feinsilver P., Kocik J., "Krawtchouk Polynomials and Krawtchouk Matrices." In: Baeza-Yates R., Glaz J., et al. (eds.), "Recent Advances in Applied Probability." Springer-Verlag, Boston, MA., pp. 115-141, 2005.
      DOI: 10.1007/0-387-23394-6_5
    • Haddad R., "A class of Orthogonal Nonrecursive Binomial Filters." IEEE Transactions on Audio and Electroacoustics, vol. 19, no. 4, 296-304, 1971.
      DOI: 10.1109/TAU.1971.1162204
    • van Lint J.H., "Introduction to Coding Theory, Third Edition." New York: Springer-Verlag, 1998.
DOI: 10.1007/978-3-642-58575-3

Related Resources

License Information