Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Search through one-dimensional cellular automata for periodic structures
ResourceFunction["AutomatonParticleDetect"][rule,seed,pad,time] tests for periodic structure after time steps of the iterator CellularAutomaton[rule] acting initially on a seed surrounded by pad values, and returns a descriptive association in case of a true positive. |
| "Canonicalize" | True | determines whether or not to post process output data |
| Method | "Structured" | specify how canonicalization handles throughput data |
Test seed {1,0,0,0,1} against the dominant periodic background of Rule 110:
| In[1]:= | ![ResourceFunction["AutomatonParticleDetect"][110, {1, 0, 0, 0, 1},
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
60, Method -> "Structured"]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/16c4159c579aee95.png) |
| Out[1]= |  |
Depict the particle as it moves through about four periods:
| In[2]:= | ![With[{positive =
ResourceFunction["AutomatonParticleDetect"][110, {1, 0, 0, 0, 1},
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
60, Method -> "Structured"]},
Labeled[ArrayPlot[
CellularAutomaton[#["Rule"],
Function[{seed, pad, len}, Flatten[
{Table[pad, {Ceiling[len/Length[pad]/2]}], seed,
Table[pad, {Ceiling[len/Length[pad]/2]}]}]
][#["Data"][[1]], #["Background"][[1]], 60], 60],
ColorRules -> {0 -> LightOrange, 1 -> Brown},
Frame -> None , PixelConstrained -> 4],
Row[{"dt: ", #["Period"], " dx: ", #["Shift"]}]
] &@positive]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/57edb27fccd3787a.png) |
| Out[2]= |  |
Detect particles in elementary Cellular Automaton Rule 110 by noting when "Result" equals True:
| In[3]:= | ![ResourceFunction["AutomatonParticleDetect"][110, IntegerDigits[#, 2],
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
60, Method -> "Structured"]["Result"] & /@ Range[5]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/1c1df7fe5b049cf9.png) |
| Out[3]= |
Make a data table for the first positive of Rule 110:
| In[4]:= | ![Grid[Transpose[{Text /@ Keys[#],
Values[#] /. List[mat__List] :> MatrixForm[List[mat]]
} &@ResourceFunction["AutomatonParticleDetect"][110, IntegerDigits[3, 2],
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
60, Method -> "Structured"]], Spacings -> {2, 2},
FrameStyle -> LightGray, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/5746c28139a59276.png) |
| Out[4]= |  |
Map over a small search space for unique particles and check their velocity statistic:
| In[5]:= | ![With[{positives = Union[Select[
ResourceFunction["AutomatonParticleDetect"][110, IntegerDigits[#, 2],
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
50, Method -> "Structured"] & /@ Range[2^5],
#["Result"] &]]},
#["Velocity"] & /@ positives]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/3a14fae1af811fc2.png) |
| Out[5]= |
Change the time parameter to run search longer and possibly find more positive results:
| In[6]:= | ![With[{positives = Union[Select[
ResourceFunction["AutomatonParticleDetect"][110, IntegerDigits[#, 2],
{0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1},
60, Method -> "Structured"] & /@ Range[2^5],
#["Result"] &]]},
#["Velocity"] & /@ positives]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/1a1f93538ea9a3b6.png) |
| Out[6]= |
For the purpose of algorithm timing analysis, it is possible to pass Method "Simple":
| In[7]:= | ![AbsoluteTiming[With[{positives = Union[Select[
ResourceFunction["AutomatonParticleDetect"][{20, {2, 1}, 2},
IntegerDigits[#, 2],
{0, 0, 0}, 150,
Method -> "Simple"
] & /@ Range[2^10],
#["Result"] &]]},
#["Velocity"] & /@ positives]]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/045cbcffd7a45632.png) |
| Out[7]= |
However, Method "Simple" is expected to be slow relative to the default "Structured":
| In[8]:= | ![AbsoluteTiming[With[{positives = Union[Select[
ResourceFunction["AutomatonParticleDetect"][{20, {2, 1}, 2},
IntegerDigits[#, 2],
{0, 0, 0}, 150,
Method -> "Structured"
] & /@ Range[2^10],
#["Result"] &]]},
#["Velocity"] & /@ positives]]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/40139ea3dc216d49.png) |
| Out[8]= |
Search for, find and depict numerous different particles in one short-time call:
| In[9]:= | ![ShallowSearchResults[code_] := With[{positives = SortBy[Union[Select[
ResourceFunction["AutomatonParticleDetect"][code,
IntegerDigits[#, 3], {0},
60, Method -> "Structured"] & /@ Range[1, 3^5],
#["Result"] &]], #["Velocity"] &]}, Labeled[ArrayPlot[
CellularAutomaton[#["Rule"],
Function[{seed, pad, len}, Flatten[
{Table[pad, {Ceiling[(len + 3)/Length[pad]/2]}], seed,
Table[pad, {Ceiling[(len + 3)/Length[pad]/2]}]}]
][#["Data"][[1]], #["Background"],
3 Max[#["Period"], 10]],
3 Max[#["Period"], 10] - 1],
ColorRules -> {0 -> LightBrown, 1 -> LightGreen, 2 -> Brown},
Frame -> None , PixelConstrained -> 4],
Row[{"dt: ", #["Period"], " dx: ", #["Shift"]}]
] & /@ positives]](https://www.wolframcloud.com/obj/resourcesystem/images/5bc/5bc2e0da-0432-40a2-b4c2-9f53bb36aec6/605aef29a066157c.png) |
| In[10]:= |
| Out[10]= | 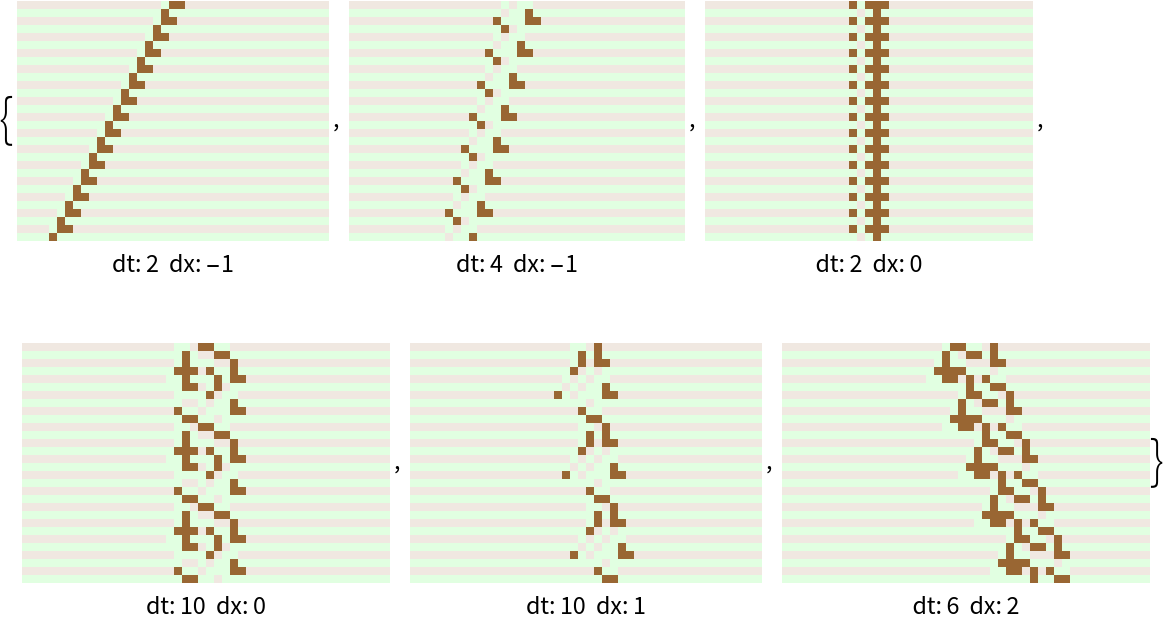 |
Look farther out and find even more remarkable results:
| In[11]:= |
| Out[11]= | 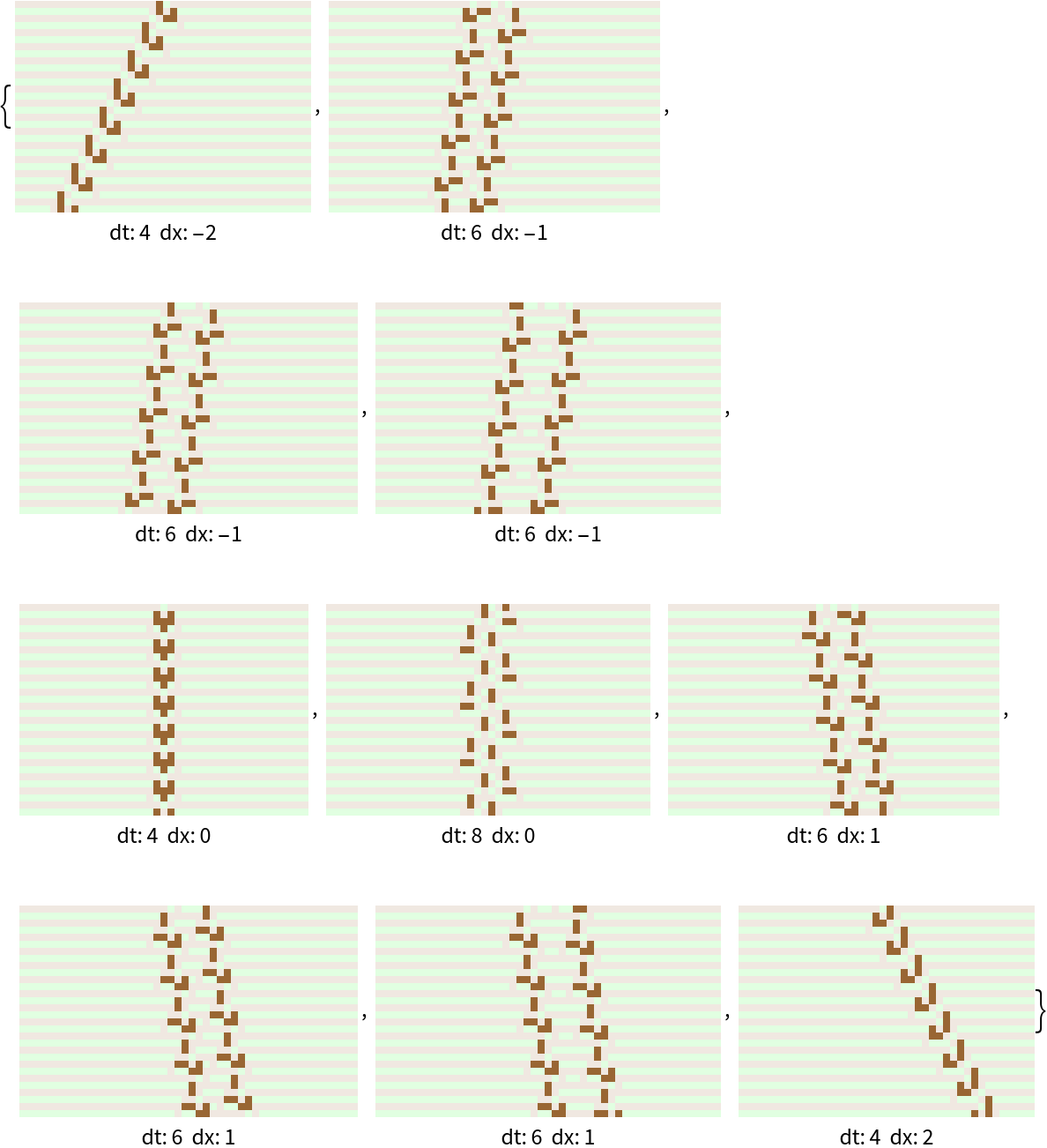 |
This work is licensed under a Creative Commons Attribution 4.0 International License