Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MeanMedianLogNormalDistribution

Source Notebook

Create a lognormal distribution using mean and median as parameters instead of the conventional parameters

Contributed by: Seth J. Chandler

ResourceFunction["MeanMedianLogNormalDistribution"][mean,median]

creates a LogNormalDistribution whose mean is mean and whose median is median.

Details and Options

The median must be less than or equal to the mean.

Examples

Basic Examples (2) 

Create a LogNormalDistribution whose mean is ⅇ3 and whose median is ⅇ:

In[1]:=
ResourceFunction["MeanMedianLogNormalDistribution"][Exp[3], Exp[1]]
Out[1]=

Create a lognormal distribution whose mean is 7000 and whose median is 2000:

In[2]:=
ResourceFunction["MeanMedianLogNormalDistribution"][7000, 2000]
Out[2]=

Scope (1) 

The function handles symbolic parameters:

In[3]:=
ResourceFunction["MeanMedianLogNormalDistribution"][(a + b + c)/3, b]
Out[3]=

Applications (1) 

Show how decreasing the median of a lognormal distribution affects the associated PDF:

In[4]:=
Table[Plot[ PDF[ResourceFunction["MeanMedianLogNormalDistribution"][1, median], x], {x, 0, 20}, PlotRange -> {0, 10}, PlotLabel -> median, ScalingFunctions -> {"Log", "Log"}], {median, 0.8, 0.2, -0.2}]
Out[4]=

Properties and Relations (2) 

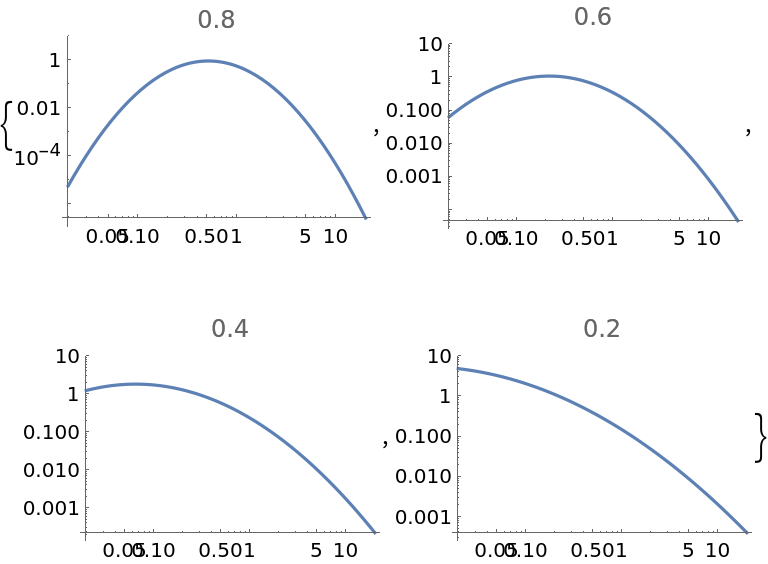An alternative parameterization would use the mean and the ratio of the median to the mean:

In[5]:=
ResourceFunction["MeanMedianLogNormalDistribution"][mean, mean*medianRatio]
Out[5]=

For other distributions, one can perform similar reparameterizations by using Solve, Reduce or similar methods:

In[6]:=
GammaDistribution[a, b] /. First@Solve[{Mean[GammaDistribution[a, b]] == m, StandardDeviation[GammaDistribution[a, b]] == s}, {a, b}]
Out[6]=

Possible Issues (1) 

If the median is greater than the mean, one gets a LogNormalDistribution with impermissible imaginary components:

In[7]:=
ResourceFunction["MeanMedianLogNormalDistribution"][3, 4]
Out[7]=

Neat Examples (2) 

Observations of health claims show that the mean is 7000 and the median is 2500. Compute the fraction of total claims incurred by persons in the top 1% of claims:

In[8]:=
With[{dist = ResourceFunction["MeanMedianLogNormalDistribution"][7000, 2500]}, 1/Mean[dist] 0.01 NExpectation[ x \[Conditioned] x > Quantile[dist, (1 - 0.01)], x \[Distributed] dist]]
Out[8]=

Make a table showing the corresponding fraction as one examines the top q percent of claims:

In[9]:=
Table[{q, With[{dist = ResourceFunction["MeanMedianLogNormalDistribution"][7000, 2500]}, 1/Mean[dist] q NExpectation[ x \[Conditioned] x > Quantile[dist, (1 - q)], x \[Distributed] dist]]}, {q, 0.01, 0.5, 0.01}]
Out[9]=

Publisher

Seth J. Chandler

Version History

  • 1.0.0 – 23 August 2019

License Information