Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MeanCurvature

Source Notebook

Compute the mean curvature of a surface

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["MeanCurvature"][s,{u,v}]

computes the mean curvature of parametrized surface s with respect to parametrizing variables u and v.

ResourceFunction["MeanCurvature"][eq,{x,y,z}]

computes the mean curvature of the surface given by the implicit equation eq in variables x,y and z.

Details

Mean curvature can be defined as the mean of the principal curvatures, while Gaussian curvature is the product of principal curvatures.
Mean curvature is an extrinsic measure of a surface and locally describes the curvature of an embedded surface.
Mean curvature can be derived as well from the first and second fundamental forms.

Examples

Basic Examples (1) 

Mean curvature of a sphere:

In[1]:=
ResourceFunction["MeanCurvature"][ Entity["Surface", "Sphere"]["ParametricEquations"][a][u, v], {u, v}] // PowerExpand
Out[1]=

Scope (2) 

Plot the Kuen surface:

In[2]:=
kuen = Entity["Surface", "KuenSurface"]["ParametricEquations"][1][u, v]
Out[2]=
In[3]:=
ks = ParametricPlot3D[Evaluate[kuen], {u, -4, 4}, {v, 0, \[Pi]}, PlotPoints -> 50]
Out[3]=

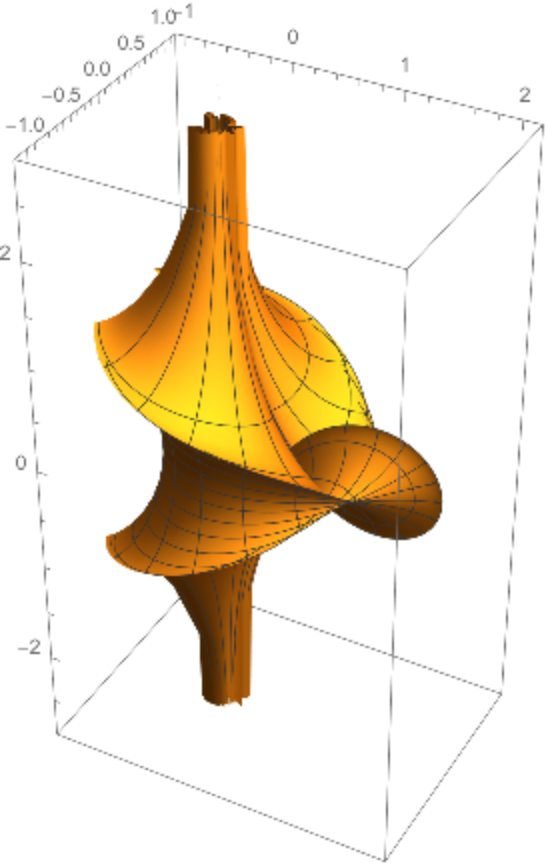
Compute its mean curvature:

In[4]:=
mc = ResourceFunction["MeanCurvature"][kuen, {u, v}] // PowerExpand
Out[4]=

Plot the mean curvature:

In[5]:=
Plot3D[Evaluate[ResourceFunction["MeanCurvature"][kuen, {u, v}]], {u, 0, 2 \[Pi]}, {v, 0, \[Pi]}, PlotPoints -> 50]
Out[5]=

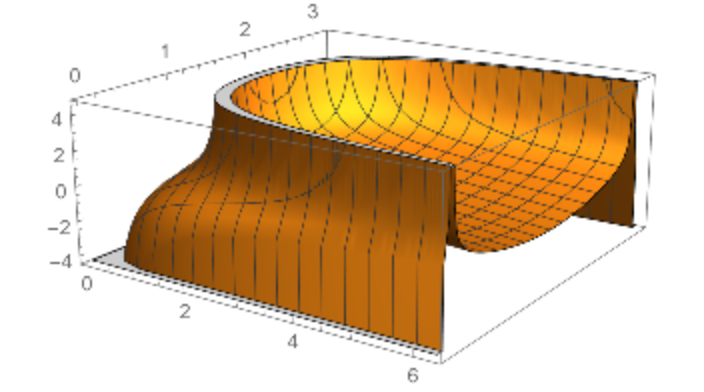
Plot the surface with a color function in accordance with the mean curvature:

In[6]:=
range = Last[PlotRange /. AbsoluteOptions[ks, PlotRange]]; ParametricPlot3D[Evaluate[kuen], {u, -4, 4}, {v, 0, \[Pi]}, PlotPoints -> 80, ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[mc, range]]], ColorFunctionScaling -> False]
Out[6]=

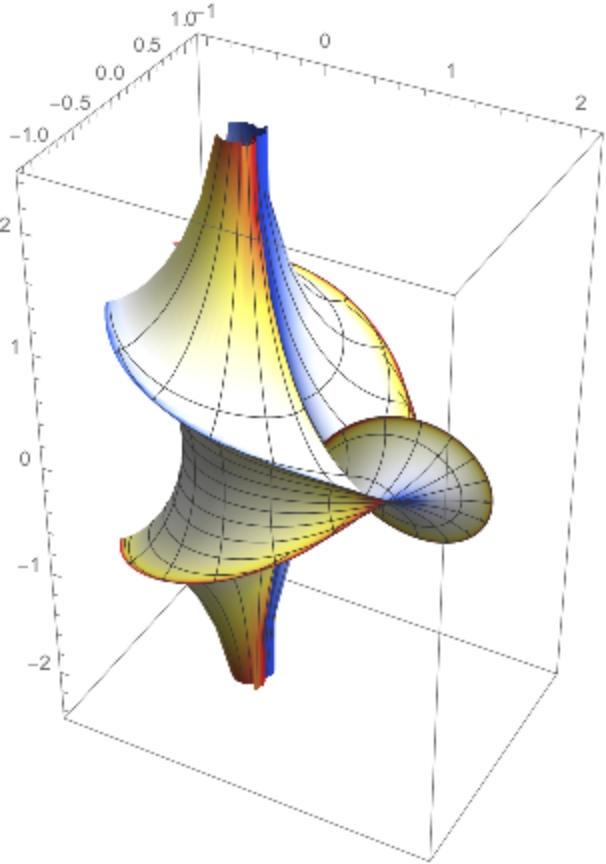
The Gaussian curvature is constant:

In[7]:=
cur = ResourceFunction["GaussianCurvature"][ Entity["Surface", "KuenSurface"]["ParametricEquations"][a][u, v], {u, v}]
Out[7]=

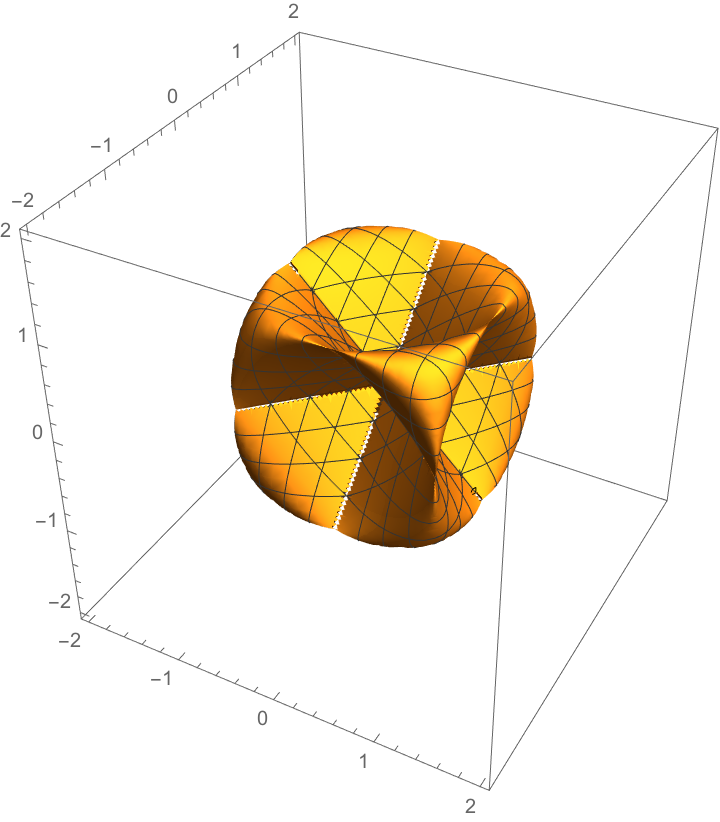
Define the implicit equation for the sine surface:

In[8]:=
sinsurfaceimplicit[a_][x_, y_, z_] := 4 x^2 y^2 (a^2 - z^2) - a^2 (x^2 + y^2 - z^2)^2

The mean curvature:

In[9]:=
ResourceFunction["MeanCurvature"][ sinsurfaceimplicit[a][x, y, z], {x, y, z}] // FullSimplify
Out[9]=
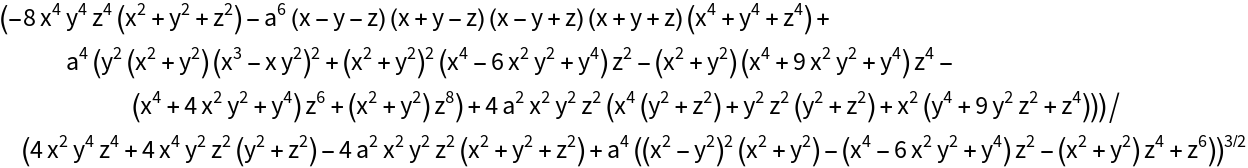
In[10]:=
ContourPlot3D[ sinsurfaceimplicit[1][x, y, z] == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotPoints -> 30]
Out[10]=

Properties and Relations (3) 

The mean curvature of a minimal surface is zero:

In[11]:=
ResourceFunction["MeanCurvature"][ Entity["Surface", "Helicoid"]["ParametricEquations"][a][u, v], {u, v}]
Out[11]=

The mean curvature for an implicit surface:

In[12]:=
ResourceFunction["MeanCurvature"][f[x, y, z], {x, y, z}] // Simplify // TraditionalForm
Out[12]=

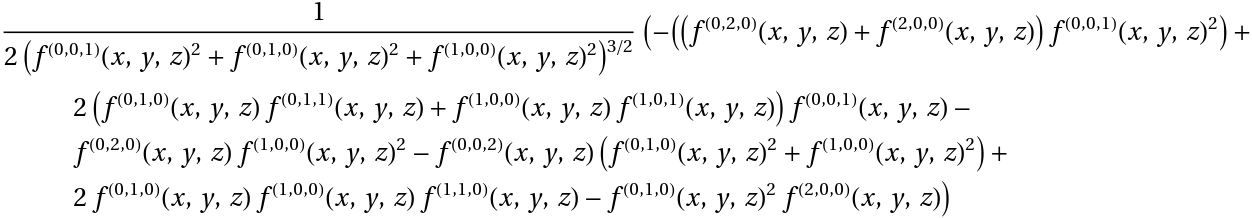
The curvature can be obtained for named surfaces using entities:

In[13]:=
Entity["Surface", "KuenSurface"]["MeanCurvature"]
Out[13]=

The expressions seem to be different, but they are equal:

In[14]:=
FullSimplify[ ResourceFunction["MeanCurvature"][ Entity["Surface", "KuenSurface"]["ParametricEquations"][a][u, v], {u, v}] - Entity["Surface", "KuenSurface"]["MeanCurvature"][a][u, v] // PowerExpand]
Out[14]=

Publisher

Enrique Zeleny

Version History

  • 1.1.0 – 19 July 2021
  • 1.0.0 – 11 March 2020

Source Metadata

  • Citation:
    • Goldman, R., Curvature formulas for implicit curves and surfaces. Computer Aided Geometric Design, 22 (7), 632–658, 2005.
      DOI:10.1016/j.cagd.2005.06.005
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information