Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Attempt to find a canonical representation for a Wolfram model
ResourceFunction["CanonicalWolframModelRule"][rule] attempts to find a canonical version of the specified Wolfram model rule. | |
ResourceFunction["CanonicalWolframModelRule"][rule,"Letter"] produces a canonical letter form of the specified Wolfram model rule. |
| 1. | Tuples are sorted by length, with longest tuples occurring first |
| 2. | Tuples of the same length on the same side of a rule are considered a rule part |
| 3. | A rule part with 3 tuples of length 2 has signature 32 |
| 4. | Rule parts are ordered so that new alphabet terms are introduced with maximal frugality |
Rename nodes and re-sort rules to find a canonical form:
| In[1]:= |
|
| Out[1]= |
|
| In[2]:= |
|
| Out[2]= |
|
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
A slightly more complicated case:
| In[5]:= |
|
| Out[5]= |
|
| In[6]:= |
![ResourceFunction[
"CanonicalWolframModelRule"][{{0, 1}, {0, 2}, {0, 3}} -> {{4, 5}, {5,
4}, {4, 6}, {6, 4}, {5, 6}, {6, 5}, {4, 1}, {5, 2}, {6, 3}, {1, 6}, {3, 4}}, "Letter"]](https://www.wolframcloud.com/obj/resourcesystem/images/5a0/5a00141a-9cae-409c-aec6-a93d20b5eada/45f3fceb2eb36062.png)
|
| Out[6]= |
|
CanonicalWolframModelRule can handle any names for elements:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
Some difficult cases:
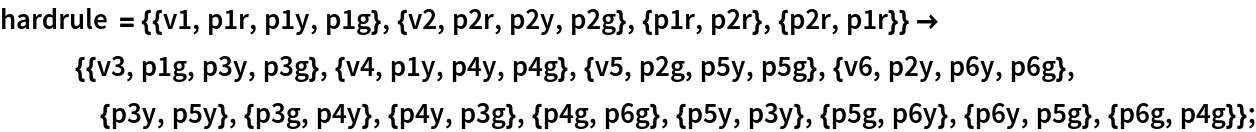
| In[9]:= |
|
| Out[9]= |
|
| In[10]:= |
|
| Out[10]= |
|

| In[11]:= |
|
| Out[11]= |

|
| In[12]:= |
|
| Out[12]= |
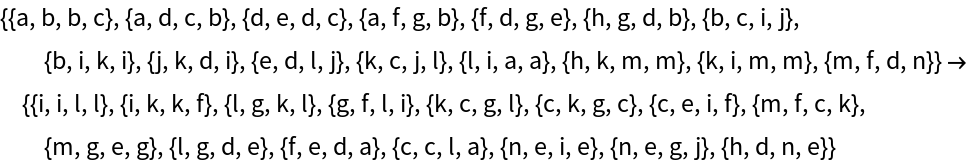
|
This work is licensed under a Creative Commons Attribution 4.0 International License