Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RecursiveFunction

Source Notebook

Obtain function values for an arbitrary recursive function

Contributed by: Bradley Klee and Thomas Adler

ResourceFunction["RecursiveFunction"][fun,inits,n]

returns the nth value of recursive fun by evaluating down to the inits.

ResourceFunction["RecursiveFunction"][fun,inits,{n1,n2,…}]

maps evaluation of fun over integer inputs {n1,n2,…}.

ResourceFunction["RecursiveFunction"][fun,inits]

is an operator form suitable for computing values of fun.

Details

The function fun must be specified as a rule: head[var]→form[var, head], where var and head are free symbols for the integer domain and range of a recursive function in some particular form. Both var and head[var] are assumed to take on integer values, usually positive.
The inits must also be specified as a rule or as a list of rules of the form: conditioni[var] → vali. When an integer value m is assigned to var, each conditioni[m] is checked by TrueQ. When one conditioni[m] evaluates to True, the function value is set as head[m]=vali.
The initial value vali can also be a function of var, i.e. conditioni[var] → vali[var], in which case a True conditioni[m] leads to the assignment head[m]=vali[m].
For example, fun=f[n]→f[n-1]+f[n-2] is the form of a typical linear recurrence with head=f, var=n, and form=Function[#2[#1-1]+#2[#1-2]]. The Fibonacci numbers have a special initial condition, inits={n<=1→n}, where condition=Function[#1<=1] with val=n. The initial condition can also be written as inits={n==0→0,n==1→1}, with two conditioni and two vali variables.
Linear recurrences such as Fibonacci are relatively easy examples. Their values can be easily computed by RecurrenceTable or RecursiveFunction. This resource RecursiveFunction can additionally compute values of nestedly recursive functions, where RecurrenceTable fails with an error message.
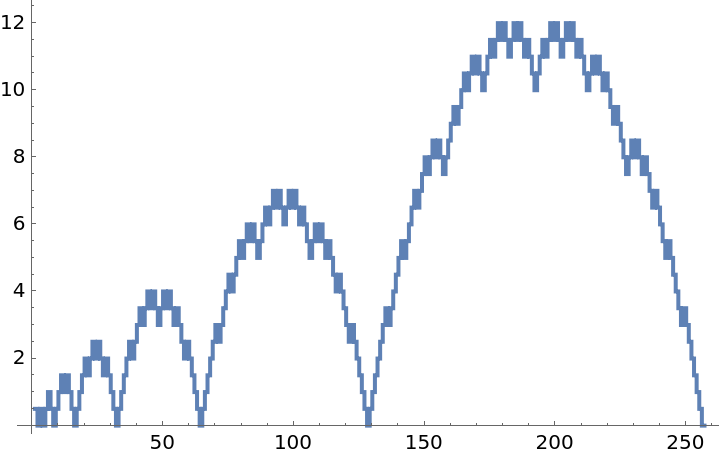
Nestedly recursive functions are recursive functions where the right-hand-side of fun contains a term like head[…] that again contains one or more instances of head[…] somewhere in its argument pattern. For example, the Hofstadter G function is defined by fun=f[n]→n-f[f[n-1]] with inits={n==0→0}.
The option Method can be set to either "Stack" or "SelfReferential". The default "Stack" method never experiences difficulties with $RecursionLimit. The "SelfReferential" method can typically compute the same data in shorter time, but might encounter TerminatedEvaluation via $RecursionLimit.
To avoid runaway iterations, it is generally assumed that evaluation of f[n] does not depend on any f[m] satisfying 0<n<m. If and when this condition becomes invalid, a Failure object is thrown. This pragmatic feature is nice to have when exploring function spaces.

Examples

Basic Examples (2) 

Generate the consecutive integers:

In[1]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, Range[10]]
Out[1]=

The tenth Fibonacci number:

In[2]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, 10]
Out[2]=

Compare with built-in functionality:

In[3]:=
SameQ[%, Fibonacci[10]]
Out[3]=

Scope (3) 

Single-Rule initial conditions do not need to be wrapped in a List:

In[4]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], \[FormalN] == 0 -> 0, Range[0, 20]]
Out[4]=

Obtain terms of the "Hofstadter G Sequence" using a nested recursive function:

In[5]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, Range[0, 20]]
Out[5]=

Compare Differences to values from a certain SubstitutionSystem:

In[6]:=
SameQ[Differences[ ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, Range[0, 33]]], Catenate[SubstitutionSystem[{1 -> {0, 1, 1}, 0 -> {0, 1}}, {1}, 3]]]
Out[6]=

Define an operator for the Hofstadter-Conway $10,000 Sequence:

In[7]:=
hcfun = ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalF][\[FormalN] - 1]] + \[FormalF][\[FormalN] - \[FormalF][\[FormalN] - 1]], {\[FormalN] == 1 -> 1, \[FormalN] == 2 -> 1}]
Out[7]=

Evaluate the function over a range of values and plot the result:

In[8]:=
ListStepPlot[hcfun[Range[256]] - Range[256]/2]
Out[8]=

Options (1) 

Setting Method to "SelfReferential" can improve computation times:

In[9]:=
AbsoluteTiming[ ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, Range[10000], Method -> #]][[1]] & /@ {"Stack", "SelfReferential"}
Out[9]=

Applications (1) 

Calculate the values of a special p-recurrence:

In[10]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1/(2 \[FormalN]^2)*((59 \[FormalN]^2 - 59 \[FormalN] + 20) \[FormalF][\[FormalN] - 1] - 12 (6 \[FormalN] - 7) (6 \[FormalN] - 5) \[FormalF][\[FormalN] - 2]), {\[FormalN] == 0 -> 1, \[FormalN] == 1 -> 10}, Range[0, 10]]
Out[10]=

Properties and Relations (3) 

Choice of Method should not affect the result (provided a TerminatedEvaluation is not met):

In[11]:=
Apply[SameQ, ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 100, Method -> #] & /@ {"Stack", "Referential"}]
Out[11]=

RecursiveFunction and RecurrenceTable agree for simple recurrences:

In[12]:=
SameQ[ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, Range[10]], RecurrenceTable[{\[FormalF][\[FormalN]] == \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], \[FormalF][0] == 0, \[FormalF][1] == 1}, \[FormalF][\[FormalN]], {\[FormalN], 1, 10}]]
Out[12]=

RecurrenceTable does not support nested recursion:

In[13]:=
RecurrenceTable[{\[FormalF][\[FormalN]] == \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], \[FormalF][0] == 0}, \[FormalF][\[FormalN]], {\[FormalN], 0, 10}] -> ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], {\[FormalN] == 0 -> 0}, Range[0, 10]]
Out[13]=

RecursiveFunction and RSolve agree for simple recurrences:

In[14]:=
SameQ[ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], {\[FormalN] <= 1 -> \[FormalN]}, Range[10]], RSolve[{\[FormalF][\[FormalN]] == \[FormalF][\[FormalN] - 1] + \[FormalF][\[FormalN] - 2], \[FormalF][0] == 0, \[FormalF][1] == 1}, \[FormalF][\[FormalN]], \[FormalN]][[1, 1, 2]] /. \[FormalN] -> Range[10]]
Out[14]=

RSolve similarly does not support nested recursion:

In[15]:=
RSolve[{\[FormalF][\[FormalN]] == \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 1]], \[FormalF][0] == 0}, \[FormalF][\[FormalN]], \[FormalN]]
Out[15]=

Possible Issues (2) 

The "SelfReferential" method can fail by exceeding $RecursionLimit:

In[16]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 1000, Method -> "SelfReferential"]
Out[16]=

The default "Stack" method never encounters $RecursionLimit failure:

In[17]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] - 1], {\[FormalN] == 0 -> 0}, 1000, Method -> "Stack"]
Out[17]=

A Failure is thrown in case of unbounded iteration:

In[18]:=
ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> 1 + \[FormalF][\[FormalN] + 1], {\[FormalN] == 0 -> 0}, 3, Method -> "Stack"]
Out[18]=

Neat Examples (5) 

Define a noisy nested recursive function:

In[19]:=
hgfun = ResourceFunction[ "RecursiveFunction"][\[FormalF][\[FormalN]] -> \[FormalN] - \[FormalF][\[FormalF][\[FormalN] - 2]], {\[FormalN] == 1 -> 0, \[FormalN] == 2 -> 1, \[FormalN] == 3 -> 1}]
Out[19]=

Choose a SampleRate that puts the primary spectrum peak on 440Hz:

In[20]:=
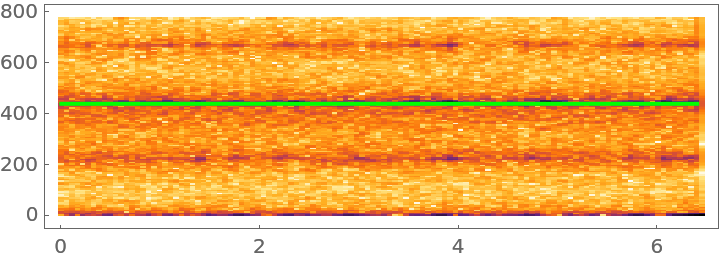
Show[ Spectrogram[hgfun[Range[10000]] - Range[10000]/GoldenRatio, SampleRate -> 1550], Plot[440, {x, 0, 6.4}, PlotStyle -> Green] ]
Out[20]=

Use ListPlay to hear what the data sounds like:

In[21]:=
ListPlay[hgfun[Range[5000]] - Range[5000]/GoldenRatio, SampleRate -> 1550, PlayRange -> All]
Out[21]=

Search the parity sequence for length-10 binary words, and reveal the hidden gems:

In[22]:=
WeaklyConnectedGraphComponents[ NearestNeighborGraph[Complement[Tuples[{1, 0}, 10], Union[Partition[Mod[hgfun[Range[50000]], 2], 10, 1]]], VertexCoordinates -> Automatic ]]
Out[22]=

Plot the missing binary words as columns in an ArrayPlot:

In[23]:=
Column[ArrayPlot[Transpose[Sort[VertexList[#]]], ImageSize -> 400] & /@ %]
Out[23]=

Publisher

Brad Klee

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 16 September 2024

Related Resources

Author Notes

Thomas Adler wrote the first version of the "Stack" method at Summer School 2024. Bradley Klee edited the "Stack" method and integrated it with the "SelfReferential" method while working on a blog with Stephen Wolfram.

License Information