Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BranchialGraphs

Source Notebook

Depict branch-like connections between components of a directed acyclic graph

Contributed by: Bradley Klee

ResourceFunction["BranchialGraphs"][g]

returns an Association of time-indexed graphs, whose edges indicate which simultaneous vertices of g have branch-like separation.

ResourceFunction["BranchialGraphs"][g,{t1,t2,…,tn}]

only computes components at times ti.

Details

ResourceFunction["BranchialGraphs"] takes the same options as Graph.
Two vertices vj and vk are have branch-like separation if g contains a vertex vi and a pair of edges vi→vj and vi→vk.
Branch-like separation is necessary, but not sufficient, for an edge between vj and vk to appear in a branchial graph of g.
A foliation of the vertices of g is a partitioning of g-vertices into time-ordered subsets (preferably also an exact cover).
Vertices vj and vk must also satisfy a simultaneity condition, which depends on choice of a foliation.
ResourceFunction["BranchialGraphs"] takes an additional option of the form: "Foliation" → {{v1,v2,…,vn}, {vn+1,vn+2,…,vn+m}, …, {vx,vx+1,…,vx+y}}.
The default "Foliation" lists a vertex in a subset as soon as its entire VertexInComponent is covered by preceding subsets.
If a specified "Foliation" lists a vertex before its entire VertexInComponent is covered by preceding subsets, the algorithm will not give a valid result.
The positions of subsets in the foliation determine their Keys in the output of ResourceFunction["BranchialGraphs"].
Provided the foliation subset at time ti includes vertices vj and vk from g, then the branchial graph at time ti will have an edge between vj and vk if and only if vj and vk have branch-like separation.

Examples

Basic Examples (4) 

Obtain the branchial graphs of a complete binary tree with four levels:

In[1]:=
ResourceFunction["BranchialGraphs"][ DirectedGraph[CompleteKaryTree[4], "Acyclic"]]
Out[1]=

Branchial graphs of a complete tertiary tree with four levels:

In[2]:=
ResourceFunction["BranchialGraphs"][ DirectedGraph[CompleteKaryTree[4, 3], "Acyclic"]]
Out[2]=

Plot a disc graph alongside its branchial graphs:

In[3]:=
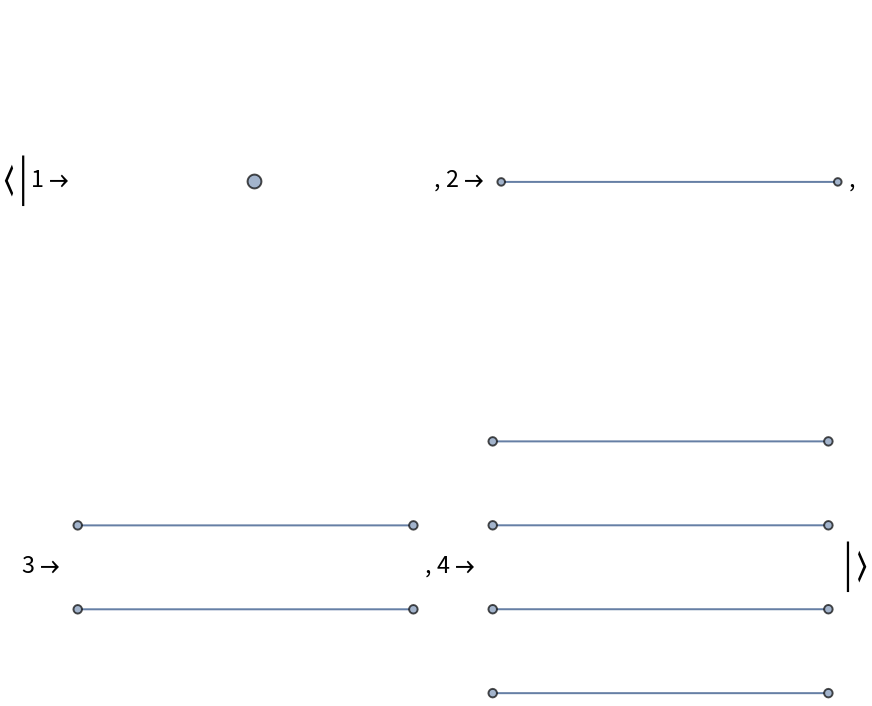
With[{g0 = NestGraph[{# + 1, 2 #, 2 # + 1} &, 1, 5]}, Column[{Graph[g0, ImageSize -> 300], "", Grid[Partition[ KeyValueMap[Labeled[Framed[Graph[#2, ImageSize -> 25], FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &, ResourceFunction["BranchialGraphs"][g0]], 8], Spacings -> {1, 1}]}, Alignment -> Center]]
Out[3]=

And changing definition slightly, plot another:

In[4]:=
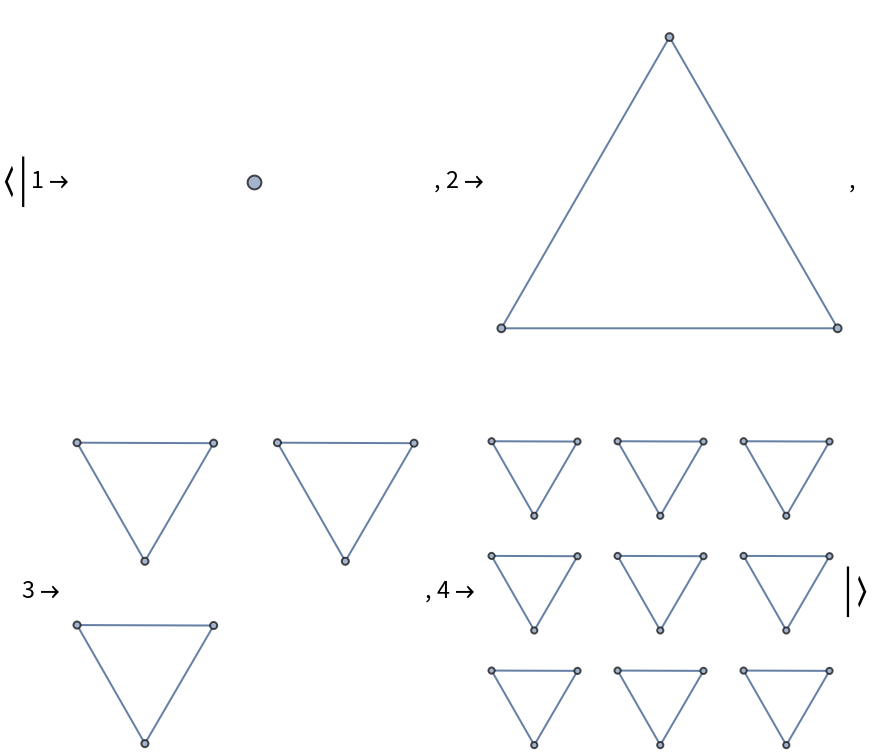
With[{g0 = NestGraph[{# + 1, 3 #, 3 # + 1, 3 # + 2} &, 1, 4]}, Column[{Graph[g0, ImageSize -> 300], "", Grid[Partition[ KeyValueMap[Labeled[Framed[Graph[#2, ImageSize -> 25], FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &, ResourceFunction["BranchialGraphs"][g0]], 8], Spacings -> {1, 1}]}, Alignment -> Center]]
Out[4]=

Obtain the branchial graphs for a RandomGraph with almost 100 vertices:

In[5]:=
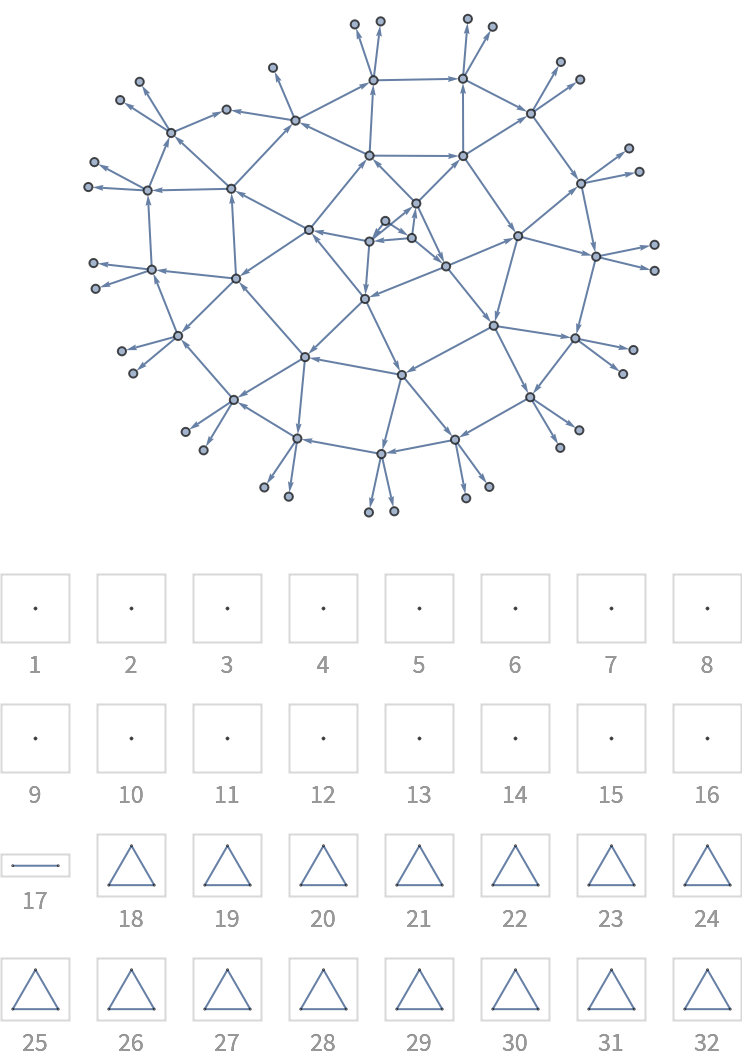
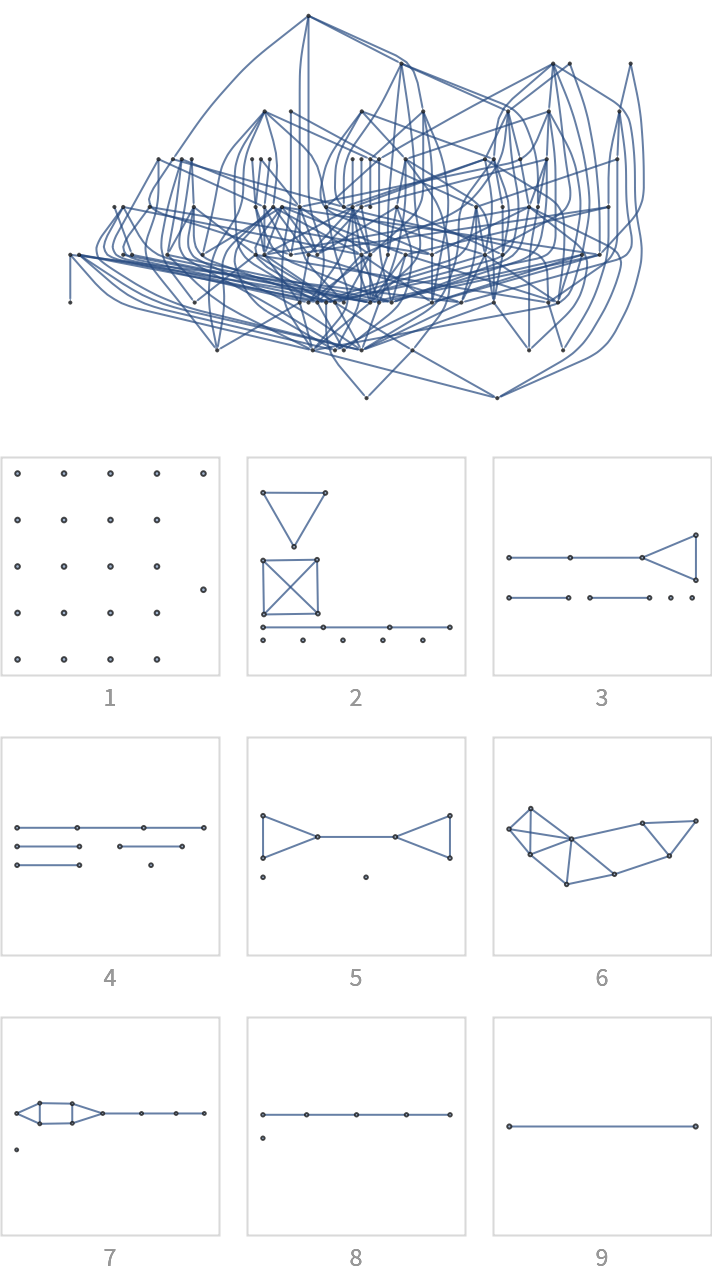
With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "", Grid[Partition[ KeyValueMap[ Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}], FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &, ResourceFunction["BranchialGraphs"][g0]], 3], Spacings -> {1, 1}]}, Alignment -> Center]]
Out[5]=

Only compute the sixth branchial graph:

In[6]:=
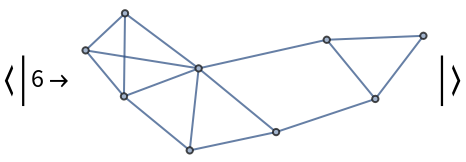
With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, ResourceFunction["BranchialGraphs"][g0, {6}]]
Out[6]=

Options (2) 

Specify foliations directly using the "Foliation" option:

In[7]:=
ResourceFunction["BranchialGraphs"][ Graph[{1 -> 2, 2 -> 3, 1 -> 4, 1 -> 5}], "Foliation" -> {{1}, {2}, {3, 4, 5}}]
Out[7]=

Compare to the default foliations in a grid:

In[8]:=
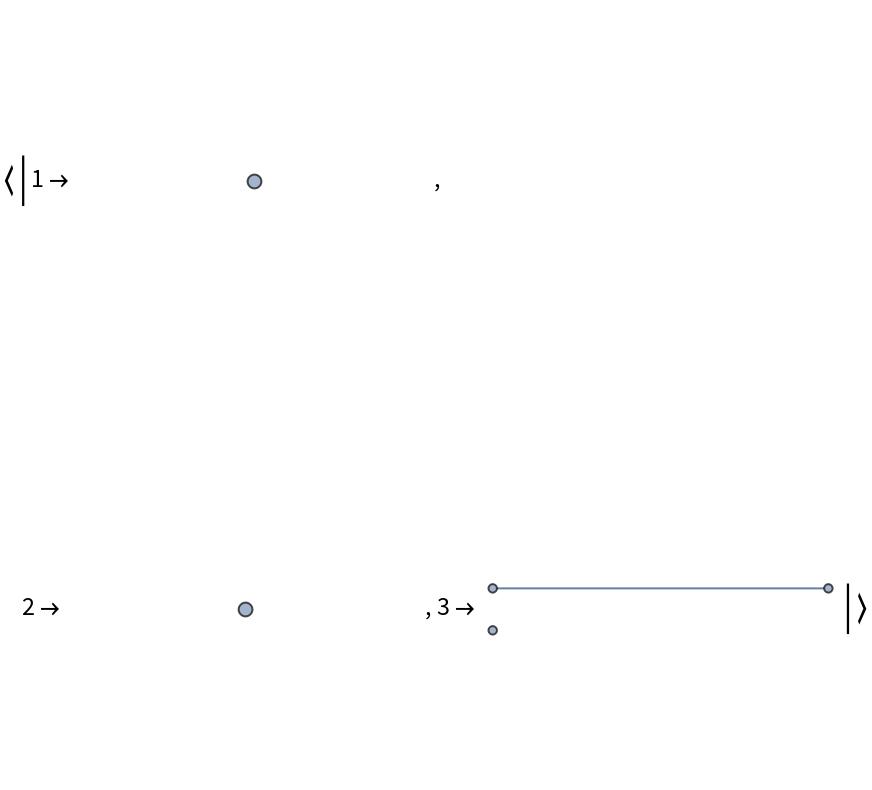
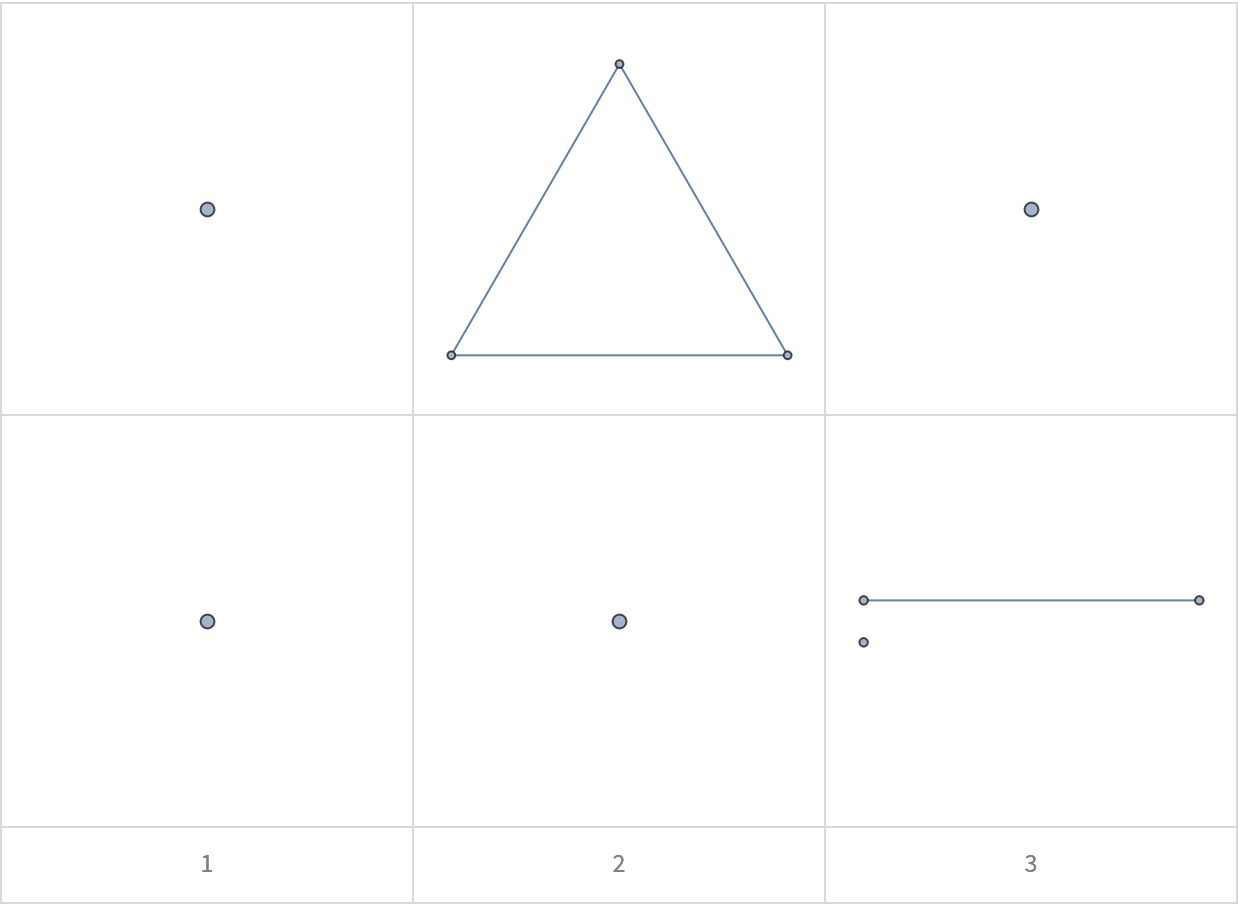
With[{g0 = Graph[{1 -> 2, 2 -> 3, 1 -> 4, 1 -> 5}]}, Grid[{Values@ResourceFunction["BranchialGraphs"][g0], Values@ResourceFunction["BranchialGraphs"][g0, "Foliation" -> {{1}, {2}, {3, 4, 5}}], Style[#, Gray] & /@ {1, 2, 3}}, Frame -> All, Spacings -> {2, 2}, FrameStyle -> LightGray]]
Out[8]=

BranchialGraphs accepts the same style options as Graph:

In[9]:=
With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, ResourceFunction["BranchialGraphs"][g0, {6}, EdgeStyle -> Darker[Magenta], VertexStyle -> Directive[EdgeForm[Darker@Purple], Lighter[Purple, .7]]]]
Out[9]=

Possible Issues (2) 

BranchialGraphs expects the input graph to be directed and acyclic:

In[10]:=
ResourceFunction["BranchialGraphs"][GridGraph[{3, 3}]]
Out[10]=

Input foliations can not include a vertex in a subset before all earlier vertices are listed in preceding subsets:

In[11]:=
ResourceFunction["BranchialGraphs"][ Graph[{1 -> 2, 2 -> 3, 1 -> 4, 1 -> 5}], "Foliation" -> {{3}, {1}, {2}, {4, 5}}]
Out[11]=

Neat Examples (3) 

Calculate the "mergial graphs" of the nine-layer RandomGraph above:

In[12]:=
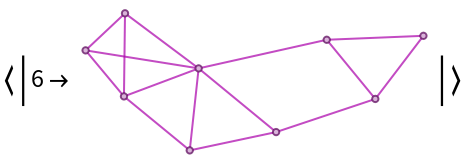
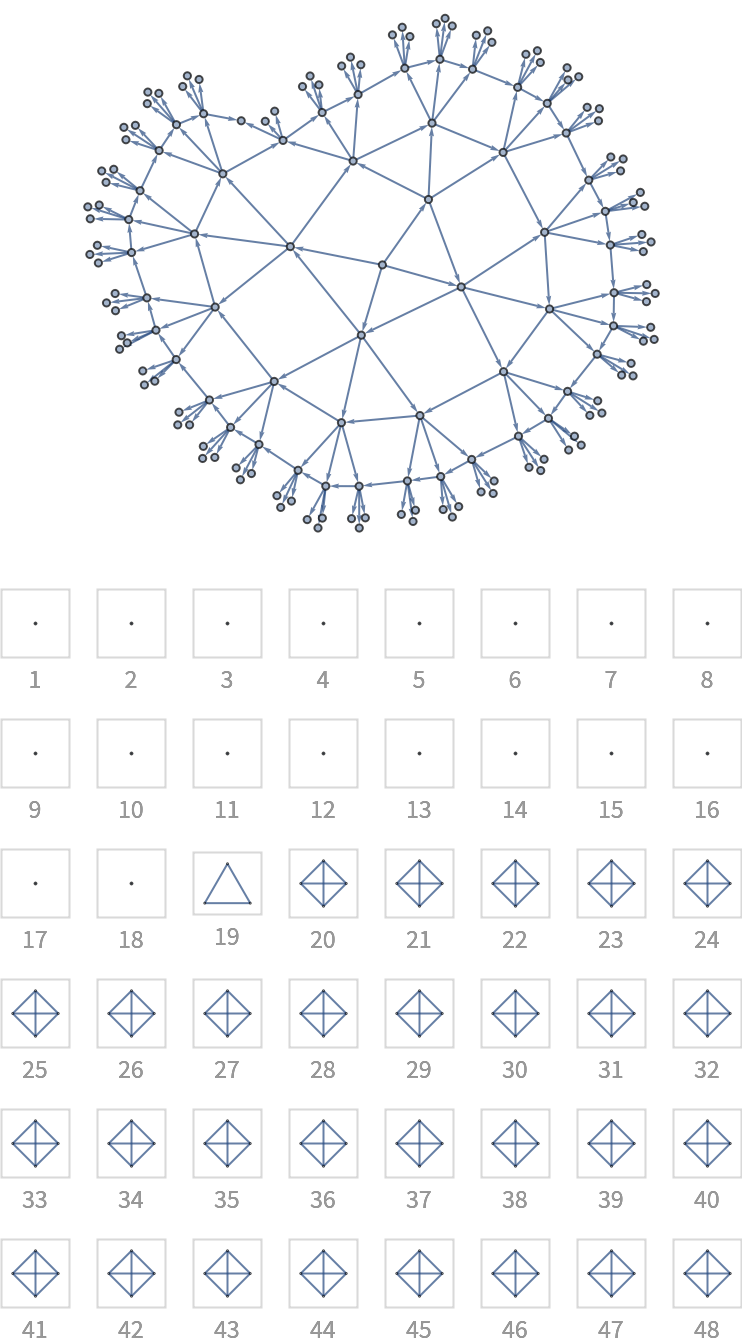
With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "", Grid[Partition[ KeyValueMap[ Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}], FrameStyle -> LightGray], Style[10 - #1, GrayLevel[0.6]]] &, Reverse@ResourceFunction["BranchialGraphs"][ReverseGraph@g0, "Foliation" -> Reverse[VertexList /@ Values[ResourceFunction["BranchialGraphs"][g0]]]] ], 3], Spacings -> {1, 1}]}, Alignment -> Center]]
Out[12]=

The mergial graphs are not simply the branchial graphs of a ReverseGraph:

In[13]:=
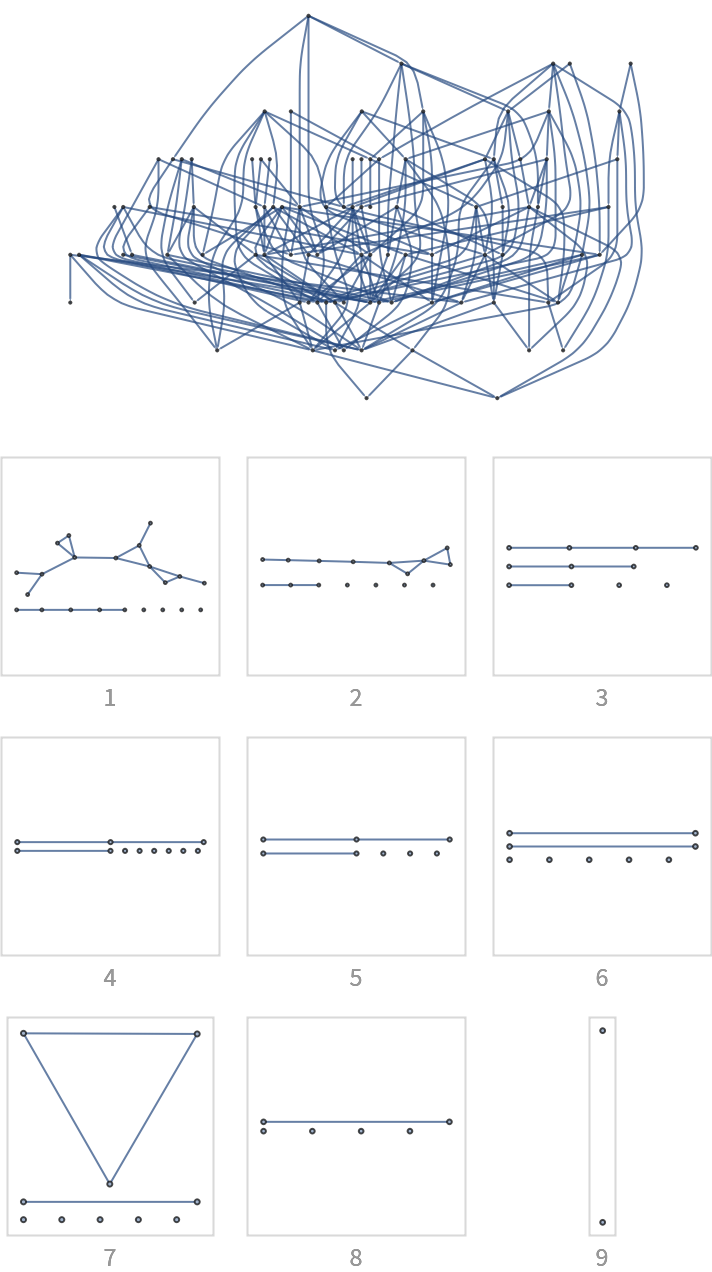
With[{g0 = (SeedRandom[12345]; ReverseGraph@First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "", Grid[Partition[ KeyValueMap[ Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}], FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &, ResourceFunction["BranchialGraphs"][g0] ], 3], Spacings -> {1, 1}]}, Alignment -> Center]]
Out[13]=

Compare where forward and reverse foliations agree:

In[14]:=
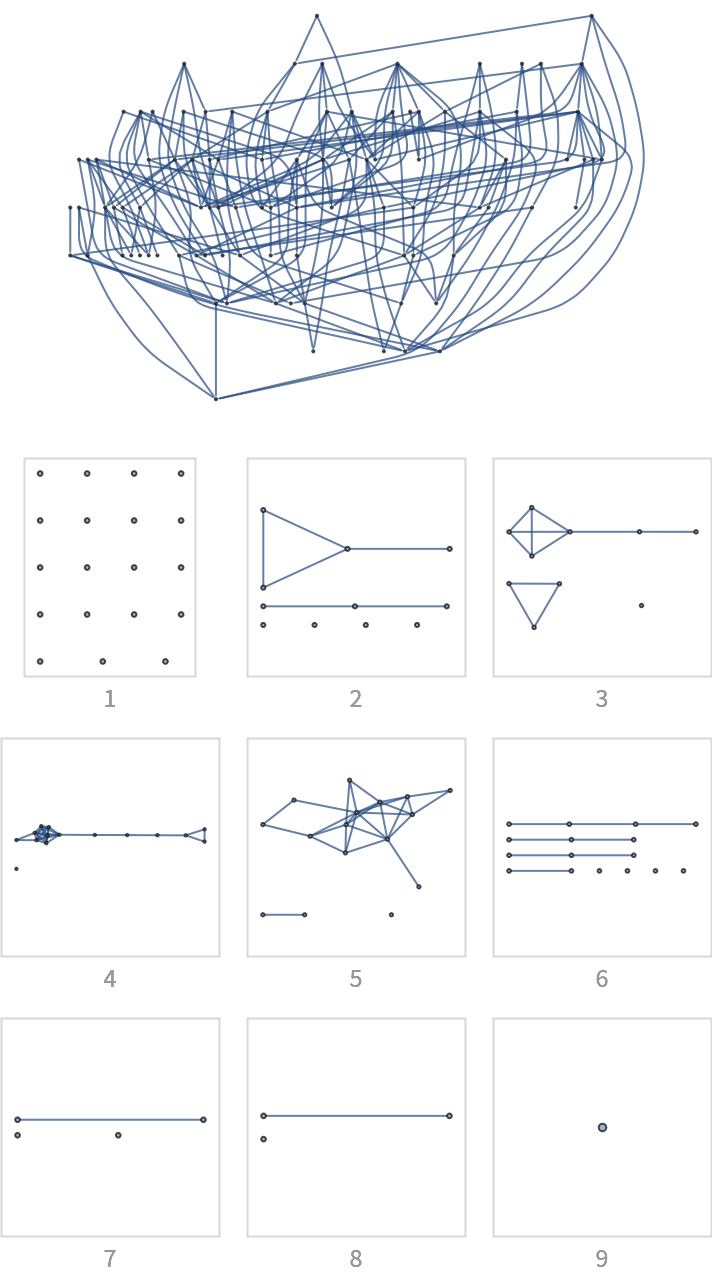
With[{ g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]]), g1 = (SeedRandom[12345]; ReverseGraph@First[WeaklyConnectedGraphComponents[ DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])}, Intersection @@@ Transpose[{VertexList /@ Values[ResourceFunction["BranchialGraphs"][g0]], Reverse[ VertexList /@ Values[ResourceFunction["BranchialGraphs"][g1]]]}]]
Out[14]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 27 June 2022

Related Resources

License Information