Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the distance between astronomical entities
ResourceFunction["AstroDistance"][entity1,entity2] computes the distance between entity1 and entity2 for the current date and time. | |
ResourceFunction["AstroDistance"][entity1,entity2,date] computes the distance between entity1 and entity2 for the specified date. | |
ResourceFunction["AstroDistance"][{entity1,…,entityn}] computes the distance between entity1 and entityn, through all the intermediate entityi, for the current date and time. | |
ResourceFunction["AstroDistance"][{entity1,…,entityn},date] computes the total distance from entity1 to entityn, through all the intermediate entityi, for the specified date. |
| "Increment" | Automatic | increment used when sampling date intervals |
| TargetUnits | Automatic | target units |
Compute the current distance between Mars and Jupiter:
| In[1]:= |
| Out[1]= |
Compute the distance between Mars and Jupiter on a specified date:
| In[2]:= |
| Out[2]= |
Compute the current total distance between entities:
| In[3]:= |
| Out[3]= |
Compute the total distance between entities on a specified date:
| In[4]:= | ![ResourceFunction[
"AstroDistance"][{Entity["Planet", "Mars"], Entity["Planet", "Jupiter"], Entity["Planet", "Saturn"], Entity["Planet", "Uranus"]}, DateObject[{2018, 9, 13}, "Day", "Gregorian", -5.`]]](https://www.wolframcloud.com/obj/resourcesystem/images/535/535d29d8-50ec-4a0c-a10c-4df769edbe87/69ea9f078c82fd4a.png) |
| Out[4]= |
Compute the distance between two objects over a range of dates:
| In[5]:= | ![ts = ResourceFunction["AstroDistance"][Entity["Planet", "Earth"], Entity["Planet", "Mars"], DateInterval[{DateObject[{2020, 1, 1}], DateObject[{2021, 1, 1}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/535/535d29d8-50ec-4a0c-a10c-4df769edbe87/3866f64330352ce8.png) |
| Out[5]= |
| In[6]:= |
| Out[6]= | 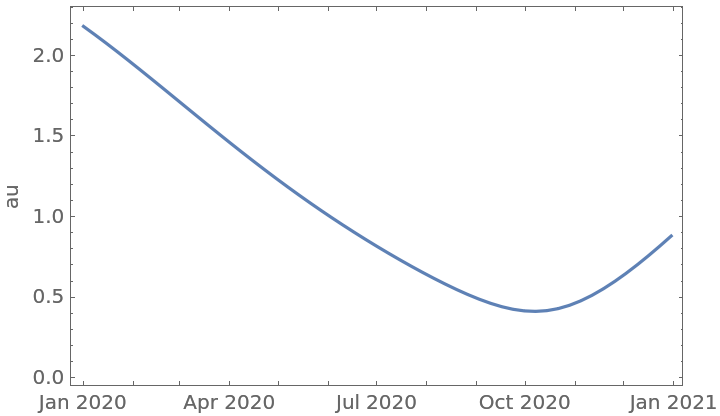 |
Entities can be in different domains:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Results are automatically given in appropriate units by default:
| In[9]:= |
| Out[9]= |
Target units can be specified:
| In[10]:= |
| Out[10]= |
Intervals of dates must be sampled in order to do the necessary computations. By default, the sampling increment is automatically determined:
| In[11]:= | ![ResourceFunction["AstroDistance"][Entity["Planet", "Earth"], Entity["Planet", "Mars"], DateInterval[{DateObject[{2020, 1, 1}], DateObject[{2021, 1, 1}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/535/535d29d8-50ec-4a0c-a10c-4df769edbe87/1d9edf34934caca0.png) |
| Out[11]= |
The number of sample points for the resulting time series can be controlled by setting the "Increment" option manually:
| In[12]:= | ![ts = ResourceFunction["AstroDistance"][Entity["Planet", "Earth"], Entity["Planet", "Mercury"], DateInterval[{DateObject[{2020, 1, 1}], DateObject[{2021, 1, 1}]}], "Increment" -> "Month"]](https://www.wolframcloud.com/obj/resourcesystem/images/535/535d29d8-50ec-4a0c-a10c-4df769edbe87/33ed8f0e1e1a2c95.png) |
| Out[12]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License