Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
This resource function is obsolete. Use the function JacobiEpsilon instead.

Function Repository Resource:

 JacobiEpsilon

Source Notebook

Evaluate the Jacobi epsilon function

Contributed by: Jan Mangaldan

ResourceFunction["JacobiEpsilon"][u,m]

gives the Jacobi epsilon function ε(u|m).

Details and Options

Mathematical function, suitable for both symbolic and numerical manipulation.
For real u, ε(u|m)=E(ϕ❘m), where , E is the EllipticE function and is the JacobiAmplitude.
ResourceFunction["JacobiEpsilon"] is a meromorphic function in both arguments.
ResourceFunction["JacobiEpsilon"] is not periodic and is therefore not strictly an elliptic function.
For certain special arguments, ResourceFunction["JacobiEpsilon"] automatically evaluates to exact values.
ResourceFunction["JacobiEpsilon"] can be evaluated to arbitrary numerical precision.
ResourceFunction["JacobiEpsilon"] automatically threads over lists.

Examples

Basic Examples (3) 

Evaluate JacobiEpsilon numerically:

In[1]:=
ResourceFunction["JacobiEpsilon"][4., 2/3]
Out[1]=

Plot the Jacobi epsilon function over a subset of the reals:

In[2]:=
Plot[ResourceFunction["JacobiEpsilon"][x, 2/3], {x, -4, 4}]
Out[2]=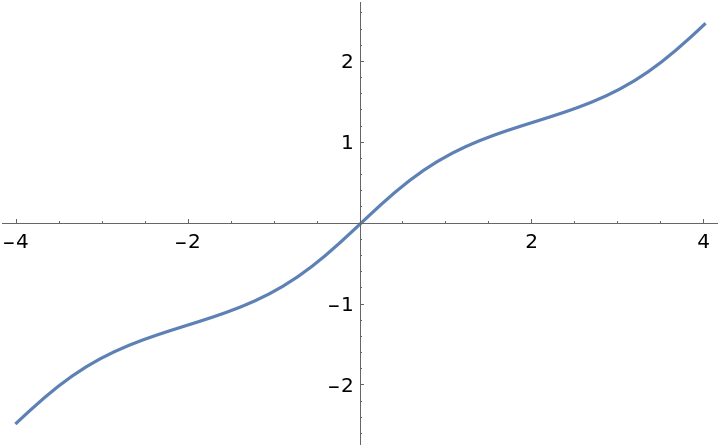

Series expansion about the origin:

In[3]:=
Series[ResourceFunction["JacobiEpsilon"][z, m], {z, 0, 8}]
Out[3]=

Scope (5) 

Evaluate for complex arguments:

In[4]:=
ResourceFunction["JacobiEpsilon"][0.2 + 0.1 I, 0.2 I]
Out[4]=

Evaluate to high precision:

In[5]:=
N[ResourceFunction["JacobiEpsilon"][Pi/3, 1/5], 50]
Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=
ResourceFunction["JacobiEpsilon"][Pi/3, 0.200000000000000000000000000]
Out[6]=

JacobiEpsilon threads elementwise over lists:

In[7]:=
ResourceFunction["JacobiEpsilon"][{\[Alpha], \[Beta]}, m]
Out[7]=

Simple exact values are generated automatically:

In[8]:=
ResourceFunction["JacobiEpsilon"][\[Phi], 0]
Out[8]=
In[9]:=
{ResourceFunction["JacobiEpsilon"][0, m], ResourceFunction["JacobiEpsilon"][EllipticK[m], m]}
Out[9]=

Parity transformation is automatically applied:

In[10]:=
ResourceFunction["JacobiEpsilon"][-u, m]
Out[10]=

Applications (3) 

Plot the Jacobi epsilon function over the complex plane:

In[11]:=
Plot3D[Im[ ResourceFunction["JacobiEpsilon"][x + I y, 1/2]], {x, -4 EllipticK[1/2], 4 EllipticK[1/2]}, {y, -4 EllipticK[1/2], 4 EllipticK[1/2]}]
Out[11]=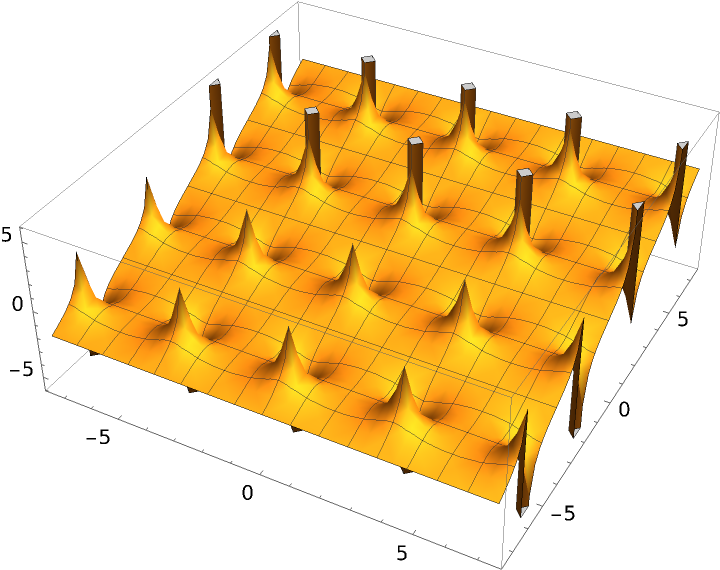

Motion of a charged particle in a linear magnetic field:

In[12]:=
With[{\[Omega] = Sqrt[v0 \[Gamma]/2]}, x[t_] = 2 \[Omega]/\[Gamma] JacobiSN[\[Omega] t, -1]; y[t_] = 2 \[Omega]/\[Gamma] (\[Omega] t - ResourceFunction["JacobiEpsilon"][\[Omega] t, -1])];

Check the solution in Newton's equations of motion with Lorentz force:

In[13]:=
{x''[t], y''[t], 0} - \[Gamma] Cross[{x'[t], y'[t], 0}, {0, 0, x[t]}] // FullSimplify
Out[13]=

Plot particle trajectories for various initial velocities:

In[14]:=
ParametricPlot[ Evaluate[Table[{x[t], y[t]} /. \[Gamma] -> 1, {v0, 1/4, 1, 1/4}]], {t, 0, 12}]
Out[14]=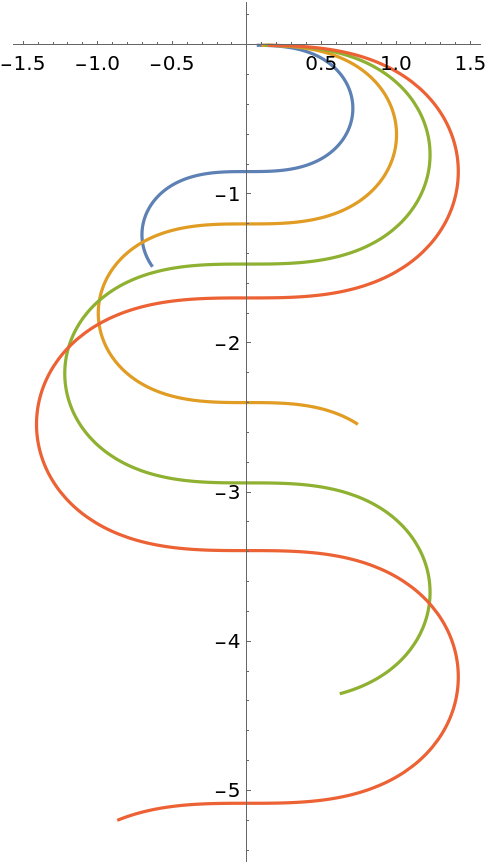

Parametrization of a rotating elastic rod (fixed at the origin):

In[15]:=
y[s_] = -2 k (JacobiCN[F, k^2] - JacobiCN[F + s \[Beta], k^2])/\[Beta]; z[s_] = s + 2 (ResourceFunction["JacobiEpsilon"][F, k^2] - ResourceFunction["JacobiEpsilon"][F + s \[Beta], k^2])/\[Beta];

Plot the shape of the deformed rod:

In[16]:=
ParametricPlot[ Evaluate[{y[s], z[s]} /. {k -> 0.96, \[Beta] -> 1, F -> 1.1}], {s, 0, 2}]
Out[16]=

Properties and Relations (1) 

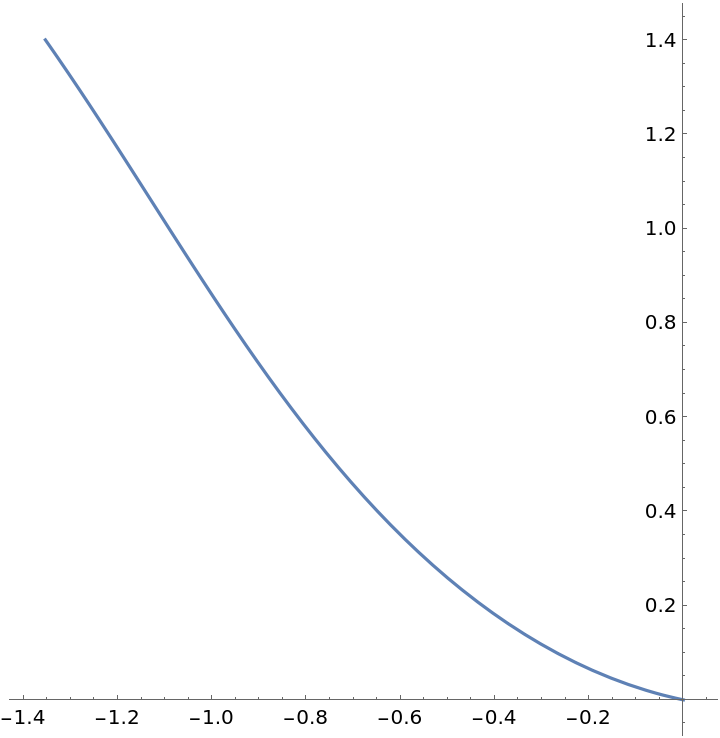ε(u|m) is a meromorphic extension of the EllipticE function :

In[17]:=
With[{m = 2/3}, Plot[{Im[ResourceFunction["JacobiEpsilon"][1 + I t, m]], Im[EllipticE[JacobiAmplitude[1 + I t, m], m]]}, {t, -7, 7}, GridLines -> {{-EllipticK[1 - m], EllipticK[1 - m]}, None}, GridLinesStyle -> Dashed]]
Out[17]=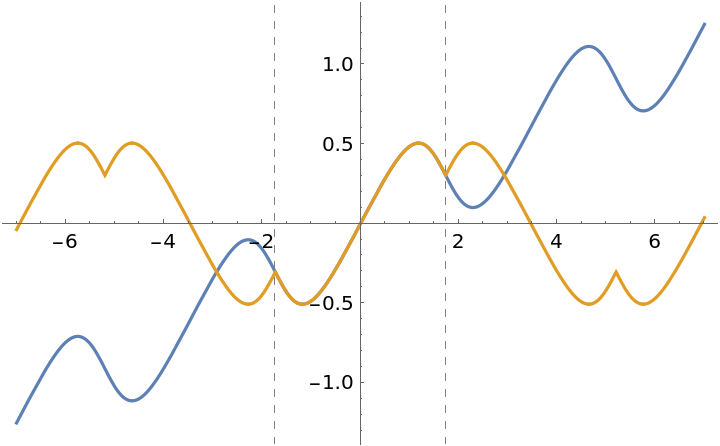
In[18]:=
With[{m = 2/3}, Plot3D[Im[ ResourceFunction["JacobiEpsilon"][x + I y, m] - EllipticE[JacobiAmplitude[x + I y, m], m]], {x, -4 EllipticK[m], 4 EllipticK[m]}, {y, -4 EllipticK[1 - m], 4 EllipticK[1 - m]}]]
Out[18]=

Possible Issues (2) 

Machine precision is not sufficient to obtain the correct result:

In[19]:=
ResourceFunction["JacobiEpsilon"][10.^13, Pi]
Out[19]=

Use arbitrary-precision arithmetic instead:

In[20]:=
N[ResourceFunction["JacobiEpsilon"][10^13, Pi], 20]
Out[20]=

Version History

  • 2.0.0 – 11 March 2020
  • 1.0.0 – 20 November 2019

Source Metadata

  • Citation:
    • "Jacobi’s Epsilon Function." §22.16(ii) in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/22.16.ii. Release 1.0.24 of 2019-09-15.

Author Notes

Some symbolic transformations (e.g. quasiperiodicity, evaluation at poles) are not yet supported. The main evaluation formula is based on formula 22.16.30 in the DLMF.

License Information