Basic Examples (1) 

Make the list of prime numbers between 50 and 300:

In[1]:=

Out[1]=

Scope (1) 

The arguments of PrimesBetween can be any real values:

In[2]:=

Out[2]=

Options (4) 

The default method is Automatic and it tries to use the fastest algorithm for the arguments provided:

In[3]:=

Out[3]=

In this case the Eratosthenes sieve method is automatically selected since it's fastest:

In[4]:=

Out[4]=

When finding a short list of large primes, nested NextPrime is automatically used since it's fastest:

In[5]:=

Out[5]=

Eratosthenes sieve is often fastest, but it requires more memory than the NextPrime method:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Applications (2) 

Find a pattern in the distribution of gaps between prime numbers:

In[8]:=

Out[9]=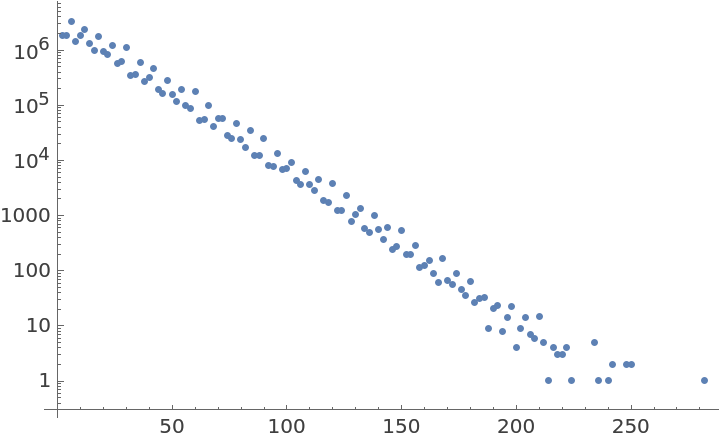

Make a list of all seven digit primes. There are over 5,000,000 of them:

In[10]:=

Out[11]=

The most common gap between primes is 6 and there are 668,765 such prime gaps:

In[12]:=

Out[13]=

There are 381,332 prime pairs separated by 2. Based on that, one might then suspect there are infinitely many primes that differ by 2. However, that is a famous conjecture that hasn't been proven true:

In[14]:=

Out[14]=

Properties and Relations (4) 

The list returned by PrimesBetween includes the arguments when they are prime:

In[15]:=

Out[15]=

PrimesBetween considers all negative integers as not prime:

In[16]:=

Out[16]=

PrimesBetween[n₁,n₂] is only defined when n₁≤n₂:

In[17]:=

Out[17]=

PrimesBetween uses Eratosthenes sieve to quickly make a list of many consecutive primes:

In[18]:=

Out[19]=

It take much longer to make the same list of primes using Table, Prime or by nesting NextPrime:

In[20]:=

Out[20]=

In[21]:=

Out[21]=

In[22]:=

Out[22]=