Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AntidiagonalMatrix

Source Notebook

Creates an antidiagonal matrix by given the antidiagonal

Contributed by: Sander Huisman

ResourceFunction["AntidiagonalMatrix"][list]

gives a matrix with the elements of list on the leading antidiagonal, and 0 elsewhere.

ResourceFunction["AntidiagonalMatrix"][list,k]

gives a matrix with the elements of list on the kth antidiagonal.

ResourceFunction["AntidiagonalMatrix"][list,k,n]

pads with 0s to create an n×n matrix.

Details and Options

ResourceFunction["AntidiagonalMatrix"][list] creates a matrix where the antidiagonal is given by the elements xi of list:

For positive k, ResourceFunction["AntidiagonalMatrix"][list,k] puts the elements k positions above the main antidiagonal. ResourceFunction["AntidiagonalMatrix"][list,-k] puts the elements k positions below.
AntidiagonalMatrix[list,k] fills the kth antidiagonal of a square matrix with the elements from list. Different values of k lead to different matrix dimensions.
ResourceFunction["AntidiagonalMatrix"][list,k,n] always creates an n×n matrix, even if this requires dropping elements of list. 
AntidiagonalMatrix[list,k,{m,n}] creates an m×n matrix.
ResourceFunction["AntidiagonalMatrix"][SparseArray[…],…] gives a SparseArray object.

Examples

Basic Examples (3) 

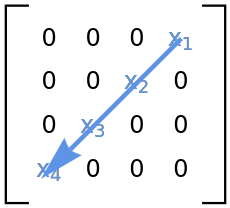
Construct an antidiagonal matrix:

In[1]:=
ResourceFunction["AntidiagonalMatrix"][{a, b, c}] // MatrixForm
Out[1]=

A super-antidiagonal matrix:

In[2]:=
ResourceFunction["AntidiagonalMatrix"][{a, b}, 1] // MatrixForm
Out[2]=

A sub-antidiagonal matrix:

In[3]:=
ResourceFunction["AntidiagonalMatrix"][{a, b}, -1] // MatrixForm
Out[3]=

Scope (4) 

The elements in AntidiagonalMatrix are chosen to match the elements of the vector:

In[4]:=
v = 1/Range[3];

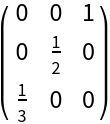
Exact number entries:

In[5]:=
ResourceFunction["AntidiagonalMatrix"][v] // MatrixForm
Out[5]=

Machine-number entries:

In[6]:=
ResourceFunction["AntidiagonalMatrix"][N[v]] // MatrixForm
Out[6]=

Arbitrary-precision number entries:

In[7]:=
ResourceFunction["AntidiagonalMatrix"][N[v, 20]] // MatrixForm
Out[7]=

When the vector is a SparseArray object, AntidiagonalMatrix will give a SparseArray object:

In[8]:=
v = SparseArray[Range[100]]
Out[8]=
In[9]:=
ResourceFunction["AntidiagonalMatrix"][v]
Out[9]=

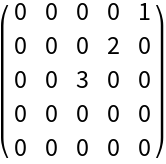
Pad with zeros to make a larger square matrix:

In[10]:=
ResourceFunction["AntidiagonalMatrix"][{1, 2, 3}, 0, 5] // MatrixForm
Out[10]=

Make a square matrix with the specified dimension:

In[11]:=
ResourceFunction["AntidiagonalMatrix"][{1, 2, 3, 4, 5}, 0, 3] // MatrixForm
Out[11]=

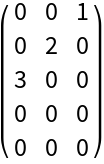
Rectangular diagonal matrices:

In[12]:=
ResourceFunction["AntidiagonalMatrix"][{1, 2, 3}, 0, {3, 5}] // MatrixForm
Out[12]=
In[13]:=
ResourceFunction["AntidiagonalMatrix"][{1, 2, 3}, 0, {5, 3}] // MatrixForm
Out[13]=

Applications (3) 

Express a matrix as the sum of its antidiagonal and off-antidiagonal parts:

In[14]:=
MatrixForm[m = Array[Subscript[a, ##] &, {3, 3}]]
Out[14]=
In[15]:=
md = ResourceFunction["AntidiagonalMatrix"][ ResourceFunction["Antidiagonal"][m]]; mo = m - md; Map[MatrixForm, {md, mo}]
Out[17]=

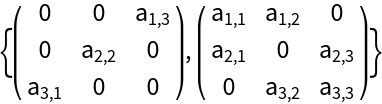
Construct a 5×5 tri-antidiagonal matrix:

In[18]:=
n = 5; MatrixForm[ ResourceFunction["AntidiagonalMatrix"][ Array[Subscript[a, #] &, n - 1], -1] + ResourceFunction["AntidiagonalMatrix"][ Array[Subscript[b, #] &, n]] + ResourceFunction["AntidiagonalMatrix"][ Array[Subscript[c, #] &, n - 1], 1]]
Out[19]=

Extract the antidiagonal from an antidiagonal rectangular matrix:

In[20]:=
m = ( { {0, a}, {b, 0}, {0, 0} } ); d = ResourceFunction["Antidiagonal"][m]
Out[21]=

Reconstruct the original matrix from the antidiagonal:

In[22]:=
ResourceFunction["AntidiagonalMatrix"][d, 0, {3, 2}] == m
Out[22]=

Properties and Relations (1) 

Using the resource function Antidiagonal with AntidiagonalMatrix gives the original vector:

In[23]:=
v = RandomReal[1, 100]; ResourceFunction["Antidiagonal"][ ResourceFunction["AntidiagonalMatrix"][v]] === v
Out[24]=

Publisher

SHuisman

Version History

  • 1.0.0 – 03 July 2019

Related Resources

License Information