Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the barycentric coordinates of a point
ResourceFunction["BarycentricCoordinates"][{p1,p2,…},q] finds the barycentric coordinates of point q in the coordinate system defined by the points pi. | |
ResourceFunction["BarycentricCoordinates"][{p1,p2,…},{q1,q2,…}] finds the barycentric coordinates for the points qi. |
Find the barycentric coordinates for the point {0.3,0.4} for the coordinate system {{1,1},{-1,1},{0,-1}}:
| In[1]:= | ![pts = {{1, 1}, {-1, 1}, {0, -1}};
p = {0.3, 0.4};
ResourceFunction["BarycentricCoordinates"][pts, p]](https://www.wolframcloud.com/obj/resourcesystem/images/50c/50c62a60-3b3f-449c-9fcb-073fe1761a34/09e3e554a42bcd4b.png) |
| Out[3]= |
Check the finding:
| In[4]:= |
| Out[4]= |
Exact input leads to exact output:
| In[5]:= |
| Out[5]= |
Calculate the values for multiple 2D points:
| In[6]:= |
| Out[6]= |
BarycentricCoordinates also works in higher dimensions:
| In[7]:= | ![ResourceFunction[
"BarycentricCoordinates"][{{-3.98, -3.56, 2.78, -1.}, {2.68, -0.44, -2.68, -2.08}, {-2.46, -1.6, -4.08, 4.78}, {-4.84, 0.04, -1.78, -1.40}, {1.18, -3.6, -0.36, -4.36}}, {-0.517, -1.702`, -1.699`, -1.068`}]](https://www.wolframcloud.com/obj/resourcesystem/images/50c/50c62a60-3b3f-449c-9fcb-073fe1761a34/6491f36e3020e709.png) |
| Out[7]= |
BarycentricCoordinates also works in very high dimensions:
| In[8]:= | ![n = 100;
pts = RandomReal[{-5, 5}, {n + 1, n}];
p = RandomReal[{-1, 1}, n];
result = ResourceFunction["BarycentricCoordinates"][pts, p]](https://www.wolframcloud.com/obj/resourcesystem/images/50c/50c62a60-3b3f-449c-9fcb-073fe1761a34/0bdefeb26d244100.png) |
| Out[11]= |  |
Check that the barycentric coordinates add up to 1:
| In[12]:= |
| Out[12]= |
Recreate the point p and subtract it from the original:
| In[13]:= |
| Out[13]= |  |
The barycentric coordinates add up to 1:
| In[14]:= | ![Total[ResourceFunction[
"BarycentricCoordinates"][{{-3.98, -3.56, 2.78, -1.}, {2.68, -0.44, -2.68, -2.08}, {-2.46, -1.6, -4.08, 4.78}, {-4.84, 0.04, -1.78, -1.40}, {1.18, -3.6, -0.36, -4.36}}, {-0.517, -1.702`, -1.699`, -1.068`}]]](https://www.wolframcloud.com/obj/resourcesystem/images/50c/50c62a60-3b3f-449c-9fcb-073fe1761a34/7aec6ffe5dbbb316.png) |
| Out[14]= |
The dimensions of the points must agree with each other:
| In[15]:= |
| Out[15]= |
The dimension of the coordinate system should be one more than the dimension of the points:
| In[16]:= |
| Out[16]= |
Interactively move the points of the coordinate system:
| In[17]:= | ![Manipulate[
Graphics[{EdgeForm[Gray], FaceForm[], Polygon[p[[;; 3]]], Red, Text[#, p[[#]] + {0, 0.25}] & /@ Range[3]}, PlotRange -> 3, PlotLabel -> ResourceFunction["BarycentricCoordinates"][p[[;; 3]], p[[4]]]], {{p, {{1, 1.4}, {-1, 1}, {0, -2}, {0.3, 0.4}}}, Locator}]](https://www.wolframcloud.com/obj/resourcesystem/images/50c/50c62a60-3b3f-449c-9fcb-073fe1761a34/282885331b5cdcec.png) |
| Out[17]= | 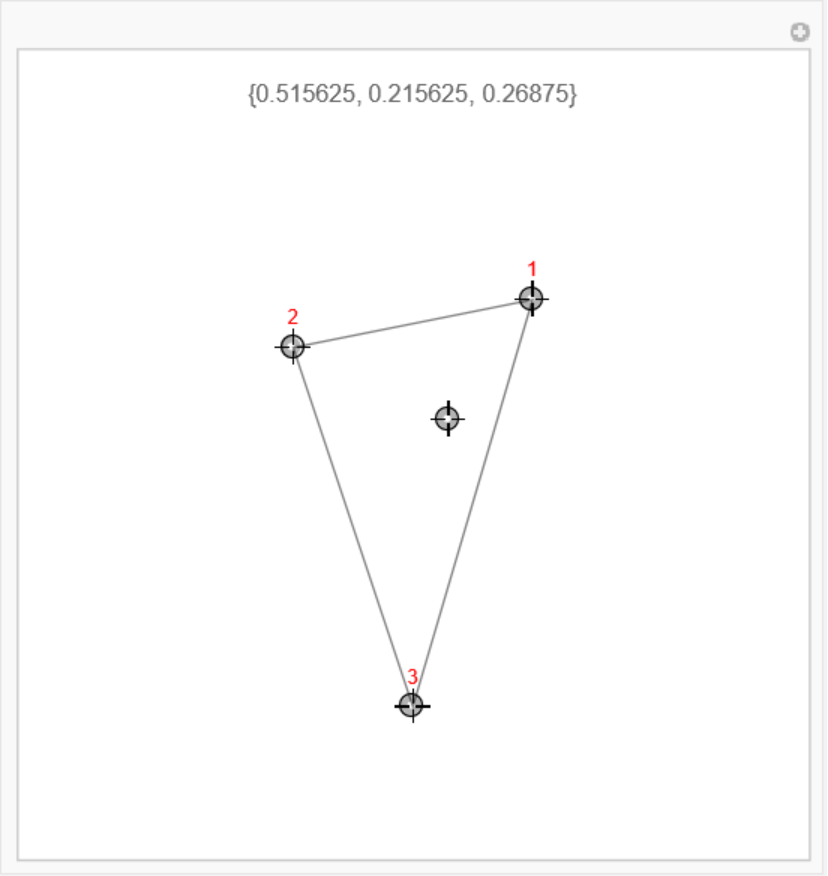 |
This work is licensed under a Creative Commons Attribution 4.0 International License