Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the canonical Knuth-Bendix completion for a given multiway system
ResourceFunction["CanonicalKnuthBendixCompletion"][rules] generates a list of canonical (i.e. initial condition-independent) Knuth-Bendix completion rules for the multiway system with the specified rules. | |
ResourceFunction["CanonicalKnuthBendixCompletion"][rules,n] generates a list of canonical (i.e. initial condition-independent) Knuth-Bendix completion rules for the multiway system with the specified rules after n steps. |
| {"lhs1"->"rhs1",…} | string substitution system |
| {{l11,l12,…}->{r11,r12,..},…} | list substitution system |
| WolframModel[rules] | Wolfram Model system |
| CellularAutomaton[rules] | cellular automaton system |
| "type"→rules | system of the specified type |
| "StringSubstitutionSystem" | rules given as replacements on strings |
| "ListSubstitutionSystem" | rules given as replacements on lists |
| "CellularAutomaton" | rules given as a list of CellularAutomaton rule specifications |
| "WolframModel" | rules given as replacements on hypergraphs |
Generate the list of all canonical Knuth-Bendix completion rules for a string substitution system:
| In[1]:= |
|
| Out[1]= |

|
Generate the list of canonical Knuth-Bendix completion rules necessary to force confluence after 2 steps:
| In[2]:= |
|
| Out[2]= |
|
CanonicalKnuthBendixCompletion can handle Wolfram models and other system types:
| In[3]:= |
|
| Out[4]= |

|
| In[5]:= |
![Take[ResourceFunction["CanonicalKnuthBendixCompletion"][
"WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 3}, {3, 3, 2}}}, 10], 20]](https://www.wolframcloud.com/obj/resourcesystem/images/4ea/4ea42bf7-02da-46a6-8a1a-191dc40deabb/2c004b48b59ddc75.png)
|
| Out[5]= |

|
Provide a cellular automaton as input:
| In[6]:= |
|
| Out[6]= |
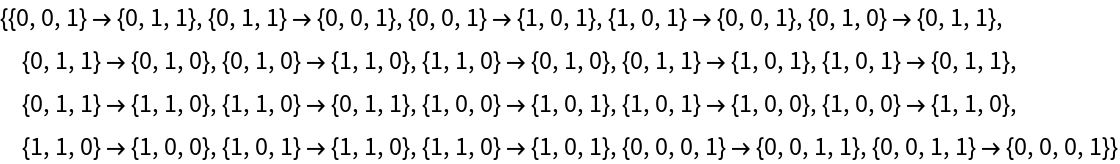
|
CanonicalKnuthBendixCompletion supports both string and list substitution systems:
| In[7]:= |
|
| Out[7]= |
|
Use substitutions on lists:
| In[8]:= |
|
| Out[8]= |
|
CanonicalKnuthBendixCompletion also supports multiway generalizations of cellular automata:
| In[9]:= |
|
| Out[9]= |

|
Generate a Knuth-Bendix completion for left- and right-shift cellular automaton rules after 5 steps:
| In[10]:= |
|
| Out[10]= |

|
Determine that the rule 30 cellular automaton is not total causal invariant:
| In[11]:= |
|
| Out[11]= |

|
CanonicalKnuthBendixCompletion also supports multiway generalizations of Wolfram Models:
| In[12]:= |
|
| Out[12]= |

|
Determine that this Wolfram model rule is not total causal invariant:
| In[13]:= |
![Take[ResourceFunction["CanonicalKnuthBendixCompletion"][
"WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 2}, {2, 2, 2}}}, 5], 20]](https://www.wolframcloud.com/obj/resourcesystem/images/4ea/4ea42bf7-02da-46a6-8a1a-191dc40deabb/77b6890d4ee5ef4d.png)
|
| Out[13]= |
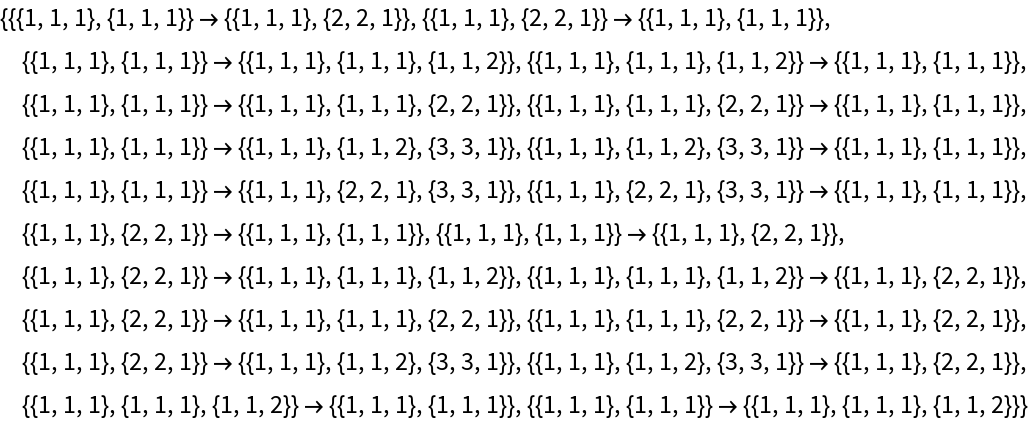
|
CanonicalKnuthBendixCompletion returns an empty list of canonical Knuth-Bendix completion rules if and only if the rule is total causal invariant:
| In[17]:= |
|
| Out[17]= |
|
| In[18]:= |
|
| Out[18]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License