Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Reflect a set of points over a line, plane or hyperplane defined by points
ResourceFunction["ReflectPoints"][mirror,pts] reflects pts across mirror. |
Reflect points about a given line:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 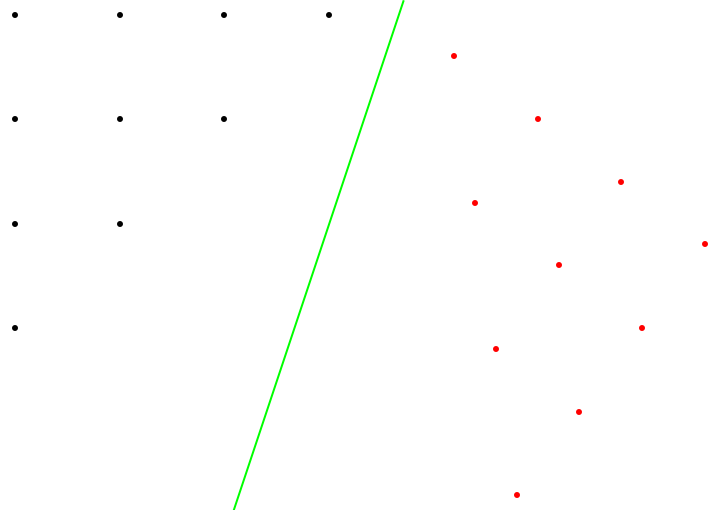 |
Reflect points about a given plane:
| In[3]:= |
| Out[3]= | 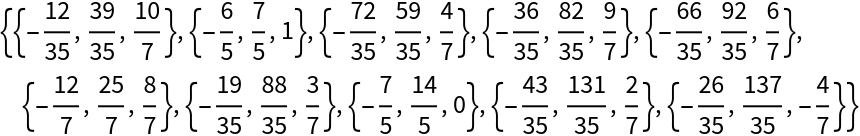 |
| In[4]:= |
| Out[4]= | 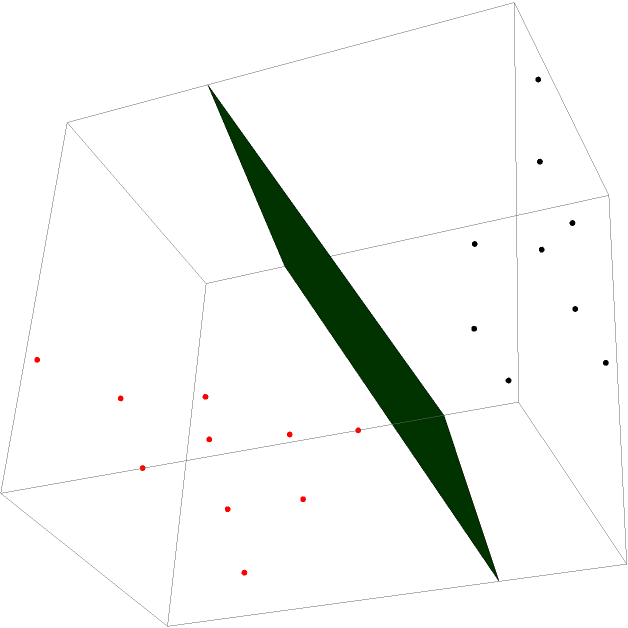 |
Reflect a single point:
| In[5]:= |
| Out[5]= |
Generate two sets of random 4D points, one representing a mirror, and the other representing points to transform:

Reflect 4D points about a hyperplane:
| In[6]:= |
| Out[6]= |  |
Construct a Hyperplane representation of the mirror:
| In[7]:= |
| Out[7]= |
Show that the distance between the points and their corresponding reflections is equal to the sum of their distances from the reflecting hyperplane:
| In[8]:= |
| Out[8]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License