Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ParallelCurve

Source Notebook

Compute parallel (offset) curves

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["ParallelCurve"][c,dis,t]

computes a parallel curve with a displacement dis from a given curve c with parameter t.

Details and Options

Parallel curves (also called offset curves) are curves that are displaced from a given curve by a real constant value, sharing the same direction of the original curve’s normal.
The parameter provided for the input curve is used as the parameter for the resulting parallel curve.

Examples

Basic Examples (2) 

One parallel curve of an ellipse:

In[1]:=
ResourceFunction["ParallelCurve"][{2 Cos[t], Sin[t]}, 1, t]
Out[1]=

Plot a variety of the ellipse's parallel curves:

In[2]:=
ParametricPlot[ Evaluate[ Table[ResourceFunction["ParallelCurve"][{2 Cos[t], Sin[t]}, s, t], {s, 0, 3, .25}]], {t, 0, 2 \[Pi]}, PlotRange -> {{-2.1, 2.1}, {-1.2, 1.2}}, Ticks -> False, Axes -> False]
Out[2]=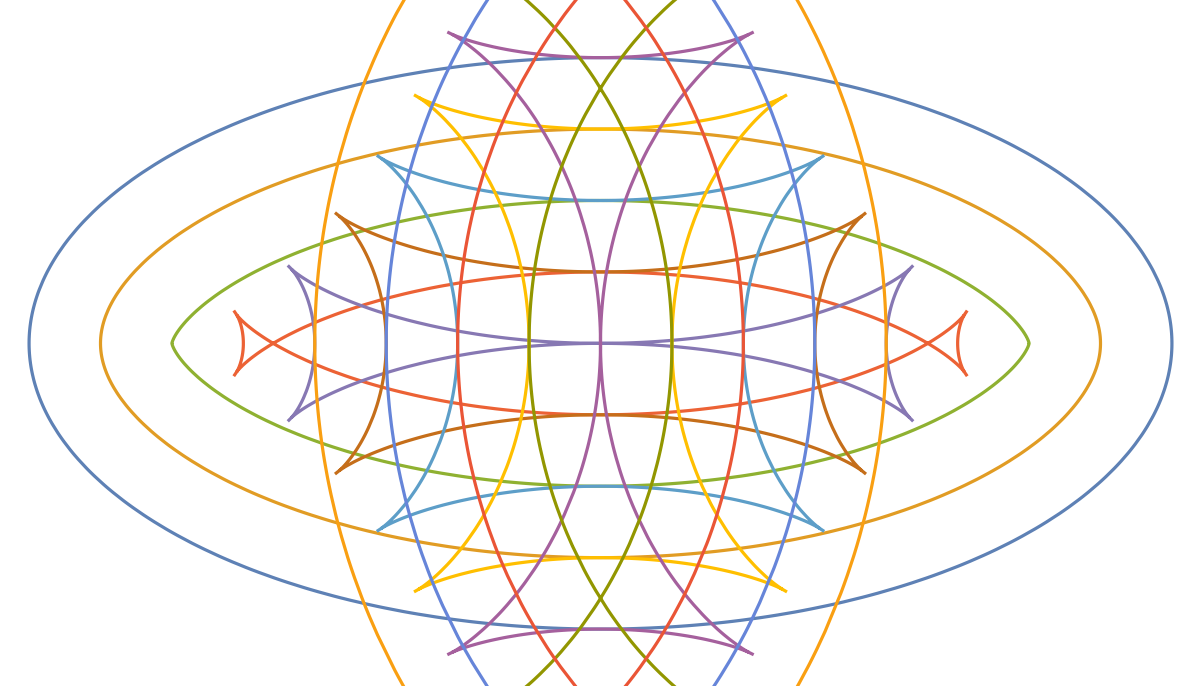

Define a limaçon:

In[3]:=
limacon = Entity["PlaneCurve", "Limacon"][ EntityProperty["PlaneCurve", "ParametricEquations"]]
Out[3]=

Plot a variety of the limaçon's parallel curves:

In[4]:=
ParametricPlot[ Evaluate[ Table[ResourceFunction["ParallelCurve"][limacon[3, 1][t], s, t], {s, 0, 4, 1}]], {t, -\[Pi], \[Pi]}, Ticks -> False]
Out[4]=

Applications (1) 

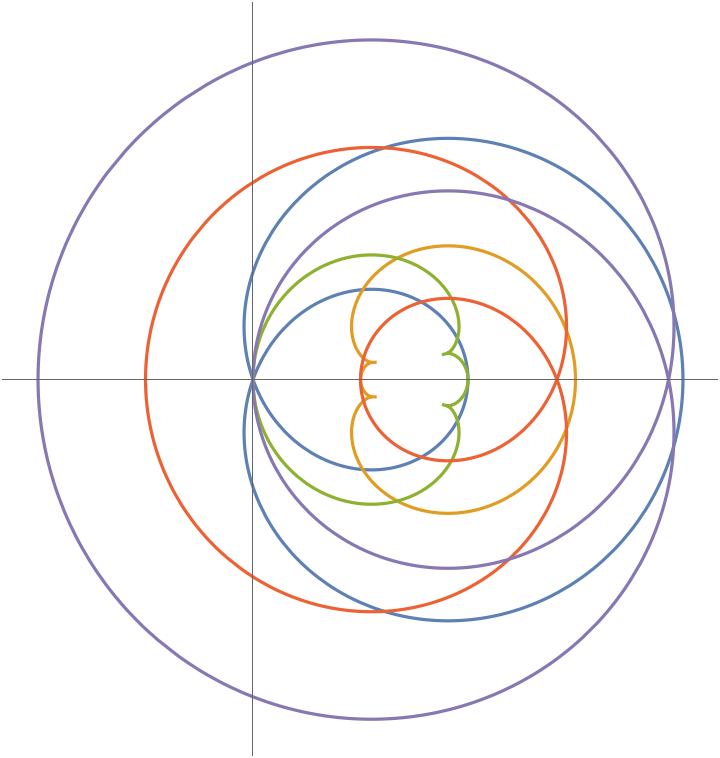Create a design using the parallel curves of a trifolium:

In[5]:=
trifolium = Entity["PlaneCurve", "Trifolium"]["ParametricEquations"][1]; ParametricPlot[ Evaluate[ Table[ResourceFunction["ParallelCurve"][trifolium[t], s, t], {s, 0, 1, .1}]], {t, -2 \[Pi], 2 \[Pi]}, Ticks -> False, Axes -> False]
Out[6]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 24 February 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information