Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Solve differential equations using one of the Runge–Kutta or related methods
ResourceFunction["RungeKuttaDSolve"][eqns,u,{x,xmin,xmax}, method] finds a numerical solution to the ordinary differential equations eqns for the function u with the independent variable x in the range xmin to xmax using the specified method. | |
ResourceFunction["RungeKuttaDSolve"][eqns,u,{x,xmin,xmax},property,method] returns a specific property for the numerical calculation. |
| "DOPRI" | Dormand–Prince method |
| "ExplicitEuler" | Forward Euler method |
| "ExplicitMidpoint" | Explicit midpoint method |
| "Heun" | Heun's method |
| "ImplicitEuler" | backward Euler method |
| "ImplicitMidpoint" | implicit midpoint method |
| "RK3" | 3rd order Runge–Kutta method |
| "RK4" | 4th order Runge–Kutta method |
| "RKBS" | Bogacki–Shampine method |
| "RKF" | Runge–Kutta–Fehlberg method |
| "Solution" | interpolation function for the solution to u |
| "Steps" | Stepwise results |
| "ButcherTableau" | Butcher tableau for the method |
Solve a differential equation using the fourth order Runge-Kutta method:
| In[1]:= |
| Out[1]= |
Find the Butcher tableau for the Dormand–Prince method:
| In[2]:= |
| Out[2]= |  |
Compute the steps to determine the interpolation function:
| In[3]:= |
| Out[3]= | 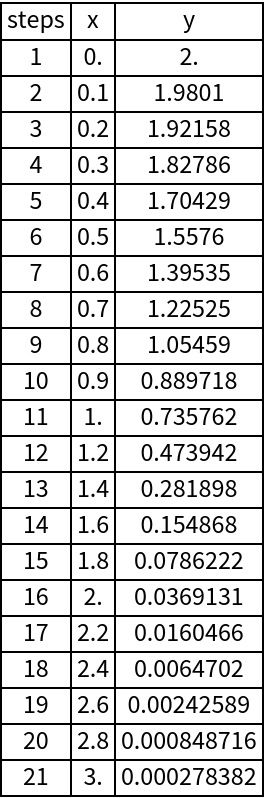 |
Get a property association of all properties:
| In[4]:= | ![ResourceFunction[
"RungeKuttaDSolve"][{x''[t] + 1/10 x'[t] + Sin[x[t]] == 1/2 Cos[t], x[0] == x'[0] == 0}, x, {t, 0, 100}, "PropertyAssociation", "ExplicitEuler"]](https://www.wolframcloud.com/obj/resourcesystem/images/49c/49cd7dfa-0f88-4737-b1a0-444a00e6432b/031627afc152c26f.png) |
| Out[4]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License