Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Display the written representation of an integer in any of several ancient number systems, including Babylonian
ResourceFunction["AncientNumberRepresentation"][n,"numsys"] gives a representation of the integer n based on the numeric system defined by "numsys". |
| "Babylonian" | Babylonian cuneiform numerals |
Give the Babylonian cuneiform representation of 59:
| In[1]:= |
| Out[1]= | 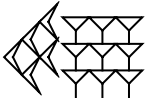 |
Give the Babylonian cuneiform representation of 2019:
| In[2]:= |
| Out[2]= | 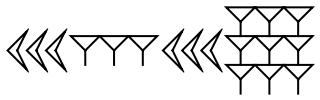 |
AncientNumberRepresentation extends the functionality of IntegerString to additional numeric systems, including some whose glyphs cannot be easily expressed in string form:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |  |
| In[6]:= |
| Out[6]= |
Around the second century BC, the Babylonians used a symbol to denote a blank space or the absence of a number:
| In[7]:= |
| Out[7]= |
The blank symbol was not, however, used in computation, meaning the numbers with equivalent base-60 expansion after the removal of zeros are indistinguishable:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |  |
AncientNumberRepresentation will return unevaluated for inapplicable arguments:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
AncientNumberRepresentation will return unevaluated for unknown numeric systems:
| In[12]:= |
| Out[12]= |
Make a table of Babylonian numerals from 1 to 59:
| In[13]:= | ![Multicolumn[
Table[Row[{n, Show[ResourceFunction["AncientNumberRepresentation"][n, "Babylonian"]]}, Spacer[10]], {n, 59}], 6, Dividers -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/488/4881b568-163e-4349-8274-f14c4821c22f/2c15224383f3a6fc.png) |
| Out[13]= | 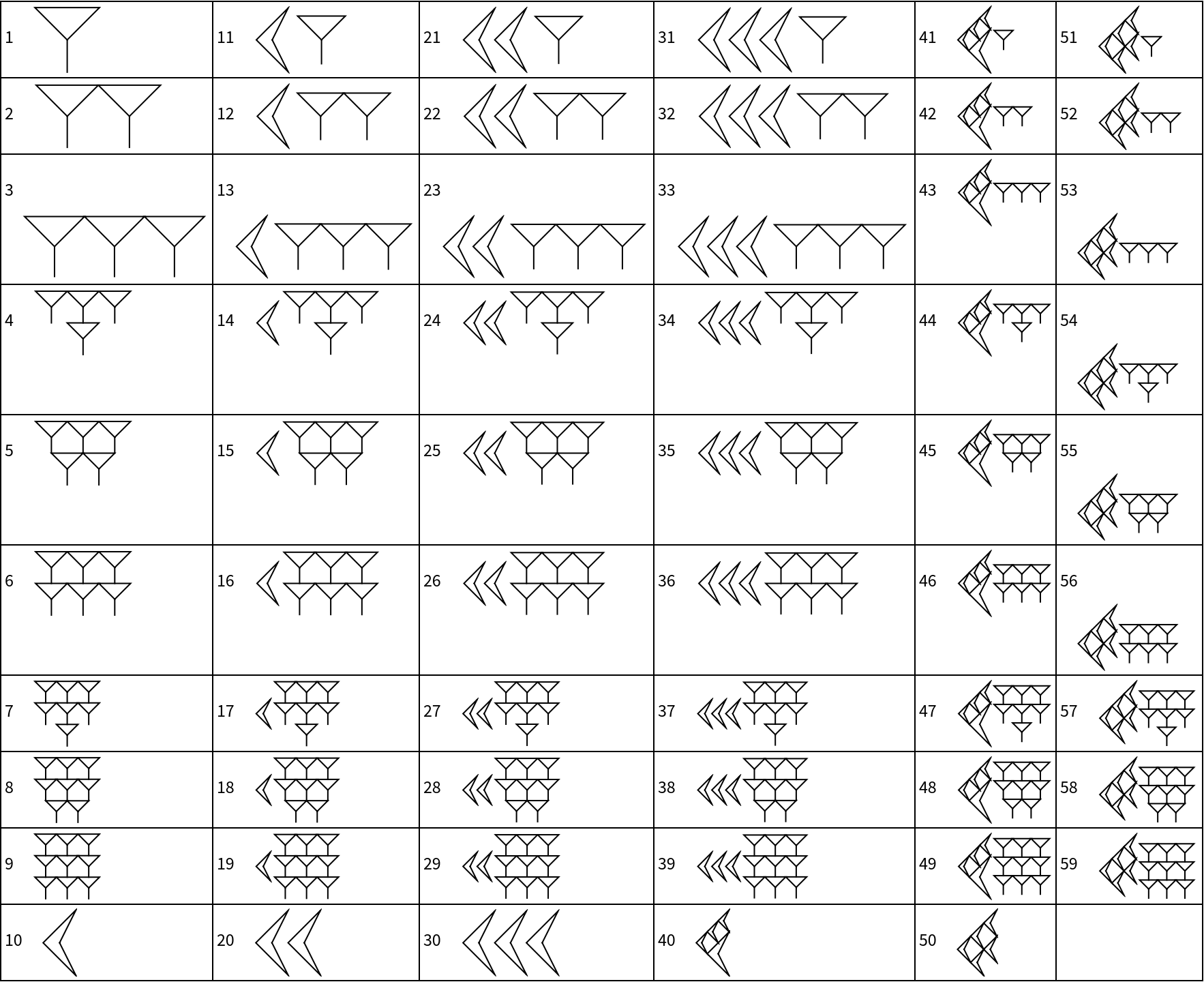 |
This work is licensed under a Creative Commons Attribution 4.0 International License