Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Symmetric tridiagonal matrix for Gaussian quadrature
ResourceFunction["GaussianQuadratureMatrix"][n] returns the n×n symmetric tridiagonal matrix that determines the abscissas and weights of the Gaussian quadrature. |
Compute the symmetric tridiagonal matrix of size 6×6:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 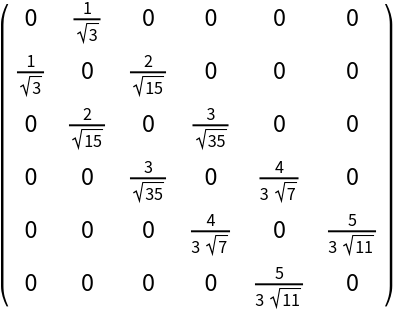 |
The abscissas and weights for the elementary n-point Gaussian quadrature are related to the eigensystem of the n⨯n symmetric tridiagonal Gaussian quadrature matrix:
| In[3]:= |
| In[4]:= |
| In[5]:= |
| Out[5]= | 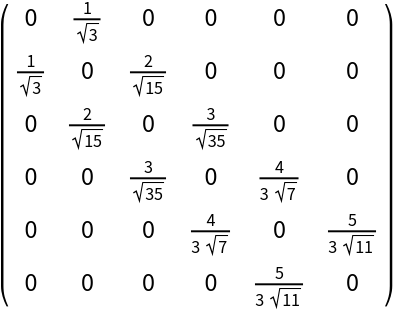 |
Eigenvalues of the matrix determine the abscissas:
| In[6]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |
Eigenvectors of the matrix determine the weights:
| In[8]:= |
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License