Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return an origin-centered simplex where the square of all edge lengths is 2
ResourceFunction["CenteredSimplex"][dim] returns an origin-centered simplex with dimension dim. |
A simplex in 3D, otherwise known as a regular tetrahedron:
| In[1]:= |
| Out[1]= |
The center is the origin and all edge-lengths are ![]() :
:
| In[2]:= |
| Out[2]= |
Show the simplex:
| In[3]:= |
| Out[3]= | 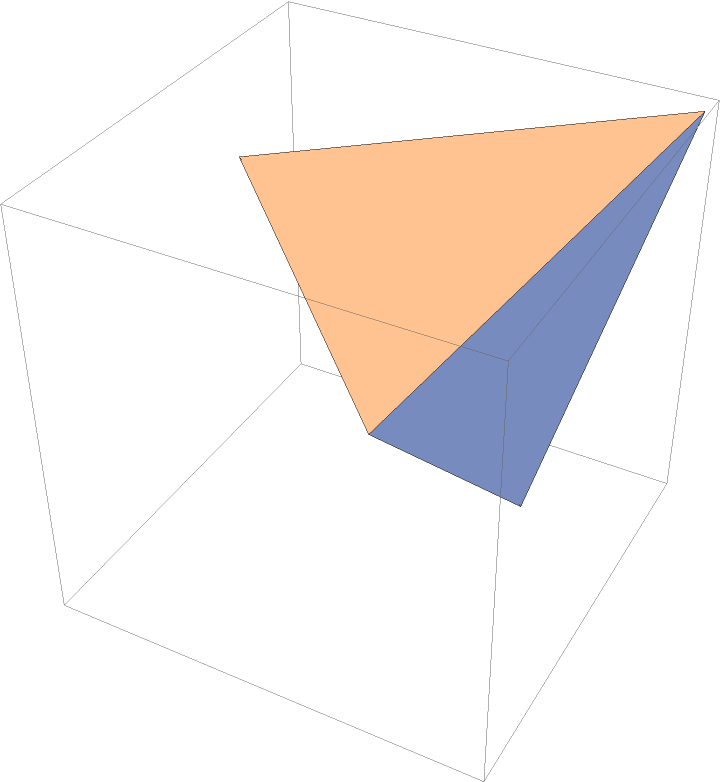 |
The last vertex of a k-dimensional CenteredSimplex output is a vector of length k with each coordinate having value ![]() :
:
| In[4]:= |
| Out[4]= | 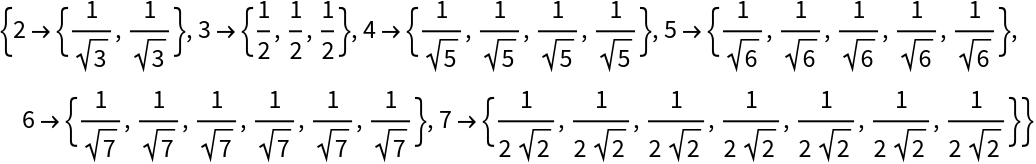 |
The other k vertices are permutations of one another:
| In[5]:= |
| Out[5]= | 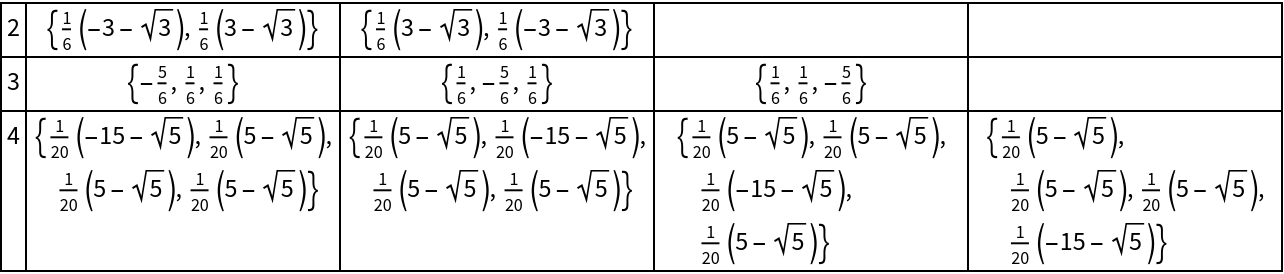 |
Select two random points in 3D space:
| In[6]:= |
| Out[6]= |
We can use the centered simplex system when converting the points to barycentric coordinates, the latter of which can be done using the resource function BarycentricCoordinates:
| In[7]:= |
| Out[7]= |
When a regular simplex with edge-lengths ![]() is used for barycentric coordinates, the Euclidean distance is preserved:
is used for barycentric coordinates, the Euclidean distance is preserved:
| In[8]:= |
| Out[8]= |
We can append ![]() to each vertex to get a square matrix:
to each vertex to get a square matrix:
| In[9]:= |
| Out[9]= |  |
This matrix has determinant 1 as well as mutually orthogonal rows and columns:
| In[10]:= |
| Out[10]= |
This work is licensed under a Creative Commons Attribution 4.0 International License