Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Given a 3D triangle, return an equivalent 2D triangle along with a transformation function
Triangle3Dto2D[triangle] computes a two-dimensional triangle along with a rotation matrix and offset vector so that one can recover triangle given in three-dimensional space. | |
Triangle3Dto2D[triangle,"TransformationFunction"] computes a two-dimensional triangle along with a TransformationFunction so that one can recover triangle given in three-dimensional space. |
Given a 3D triangle, generate a 2D triangle, a matrix and an offset:
| In[1]:= |
|
| Out[1]= |
|
Calculate some results in 2D, then return to 3D:
| In[2]:= |
|
| Out[2]= |
|
Generate a 2D triangle and a transformation function from a 3D triangle:
| In[3]:= |
|
| Out[3]= |

|
Calculate some results in 2D, then return to 3D:
| In[4]:= |
|
| Out[4]= |
|
The matrix and offset can be discarded:
| In[5]:= |
|
| Out[5]= |
|
| Out[6]= |
|
Show both triangles in a 3D graphic:
| In[7]:= |
|
| Out[7]= |

|
Find triangles of a polyhedron:
| In[8]:= |
|
Look at the 2D triangle for one of them:
| In[9]:= |
|
| Out[9]= |
|
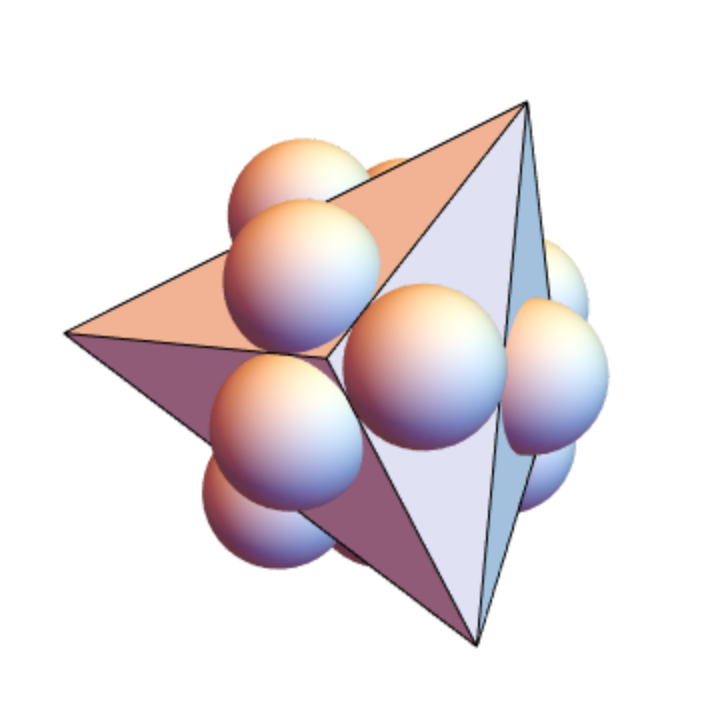
Draw tangent spheres on each triangle:
| In[10]:= |
![centers = Table[{tri, tf} = ResourceFunction["Triangle3DTo2D"][polytris[[n]], "TransformationFunction"]; results2D = {Insphere[tri][[1]]}; Simplify[tf[PadRight[results2D, {Automatic, 3}]]], {n, 1, 12}]; Graphics3D[{Polygon[polytris], Sphere[Flatten[centers, 1], 5/(6 Sqrt[11])]}, Boxed -> False, SphericalRegion -> True, ViewAngle -> Pi/8]](https://www.wolframcloud.com/obj/resourcesystem/images/459/459e11f6-144f-4bda-8b19-b593139256ce/18b48a1849f2873f.png)
|
| Out[10]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License