Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the complete conditional distribution of a variable in a statistical model
ResourceFunction["CompleteConditionalDistribution"][{Distributed[v1,dist1],Distributed[v2,dist2],…},vi] gives the distribution of vi conditional on v1,v2,…. |
Compute the conditional probability of a beta-distributed variable:
| In[1]:= |
| Out[1]= |
Derive the formula for gamma-Poisson conjugacy:
| In[2]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Lambda] \[Distributed] GammaDistribution[\[Alpha], \[Beta]],
x \[Distributed] PoissonDistribution[\[Lambda]]
},
\[Lambda]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/7f53def3c6317c61.png) |
| Out[2]= |
Add a constant multiplier:
| In[3]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Lambda] \[Distributed] GammaDistribution[\[Alpha], \[Beta]],
x \[Distributed] PoissonDistribution[\[Lambda]*c]
},
\[Lambda]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/67a1707e6422474c.png) |
| Out[3]= |
Compute a conditional distribution that is not a named distribution:
| In[4]:= | ![\[ScriptCapitalD] = ResourceFunction["CompleteConditionalDistribution"][{
x \[Distributed] PoissonDistribution[\[Lambda]],
y \[Distributed] GammaDistribution[x, \[Beta]]
},
x,
Assumptions -> y > 0
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/4ffa0aeffdbe7ffa.png) |
| Out[4]= | 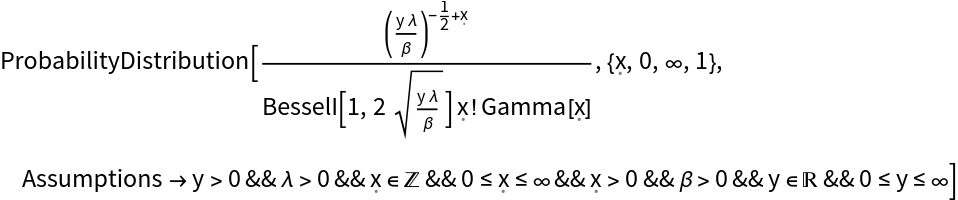 |
Compute properties of the resulting distribution:
| In[5]:= |
| Out[5]= | 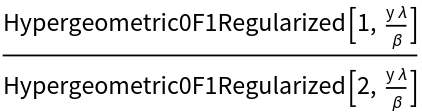 |
| In[6]:= |
| Out[6]= | 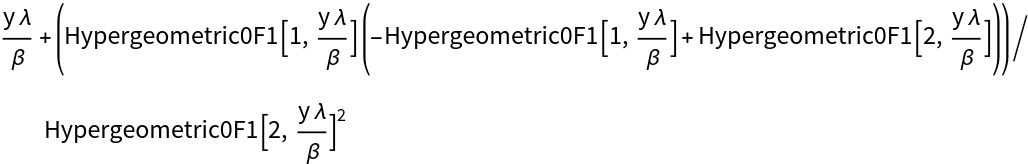 |
Derive the formula for normal-normal conjugacy:
| In[7]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Mu] \[Distributed] NormalDistribution[\[Mu]1, \[Sigma]1],
x \[Distributed] NormalDistribution[\[Mu], \[Sigma]]
},
\[Mu]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/1d5d2410ceb75b57.png) |
| Out[7]= |
Derive the formula for normal-inverse gamma conjugacy:
| In[8]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Sigma]2 \[Distributed] InverseGammaDistribution[\[Alpha], \[Beta]],
x \[Distributed] NormalDistribution[\[Mu], Sqrt[\[Sigma]2]]
},
\[Sigma]2
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/63ac8323ee015851.png) |
| Out[8]= |
Compute multiple conjugate relationships for one model:
| In[9]:= | ![model = {
\[Mu] \[Distributed] NormalDistribution[\[Mu]1, \[Sigma]1],
\[Sigma]2 \[Distributed] InverseGammaDistribution[\[Alpha], \[Beta]],
x \[Distributed] NormalDistribution[m \[Mu] + b, Sqrt[\[Sigma]2]]
};](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/484480e503c659eb.png) |
| In[10]:= |
| Out[10]= | 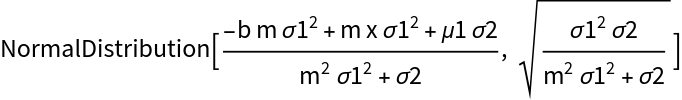 |
| In[11]:= |
| Out[11]= |
Derive an update for a beta-binomial model based on multiple observed values:
| In[12]:= | ![ResourceFunction["CompleteConditionalDistribution"][{
p \[Distributed] BetaDistribution[\[Alpha], \[Beta]],
Table[Indexed[x, i] \[Distributed] BinomialDistribution[n, p], {i, 5}]
},
p
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/67c4e9c79615c6ea.png) |
| Out[12]= |
Derive an update for a normal-normal model based on multiple observed values:
| In[13]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Mu] \[Distributed] NormalDistribution[\[Mu]0, \[Sigma]0],
Table[
Indexed[x, i] \[Distributed] NormalDistribution[\[Mu], \[Sigma]], {i, 5}]
},
\[Mu]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/6ecc129c82428147.png) |
| Out[13]= | 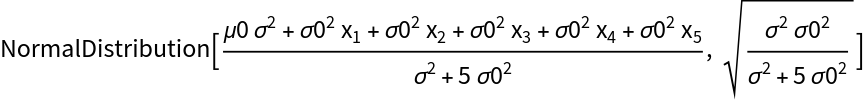 |
Derive an update for a gamma-Poisson model based on multiple observed values:
| In[14]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Lambda] \[Distributed] GammaDistribution[\[Alpha], \[Beta]],
Table[
Indexed[x, i] \[Distributed] PoissonDistribution[\[Lambda]*c], {i,
5}]
},
\[Lambda]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/680e8c34dd5530d5.png) |
| Out[14]= |
Derive gamma-gamma conjugacy:
| In[15]:= | ![Simplify@ResourceFunction["CompleteConditionalDistribution"][{
\[Beta] \[Distributed] GammaDistribution[\[Alpha]0, 1/\[Beta]0],
x \[Distributed] GammaDistribution[\[Alpha], 1/\[Beta]]
},
\[Beta]
]](https://www.wolframcloud.com/obj/resourcesystem/images/430/4306a40f-8126-43cb-996a-cb320790369a/0f915964d45d2869.png) |
| Out[15]= |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License