Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Plot the function together with a graphical display of the Newton iterations approximating its root
ResourceFunction["NewtonMethodPlot"][f,{x,xmin,xmax},pt] returns a plot of f from x=xmin to x=xmax, together with illustrations representing the iterations of Newton’s root-finding method, starting at x=pt. |
| "DrawGraph" | True | whether to include the graph |
| "Iterations" | 5 | the number of iterations to perform |
| "LineStyle" | Thick | graphics directive to specify the style for the line |
| "PointStyle" | PointSize[0.016] | graphics directive to specify the style for the point |
| "PrintDisplay" | True | whether to include the table of iteration values |
| WorkingPrecision | MachinePrecision | determines the number of digits used in internal calculations |
Illustrate Newton’s method on a simple function:
| In[1]:= |
| Out[1]= | 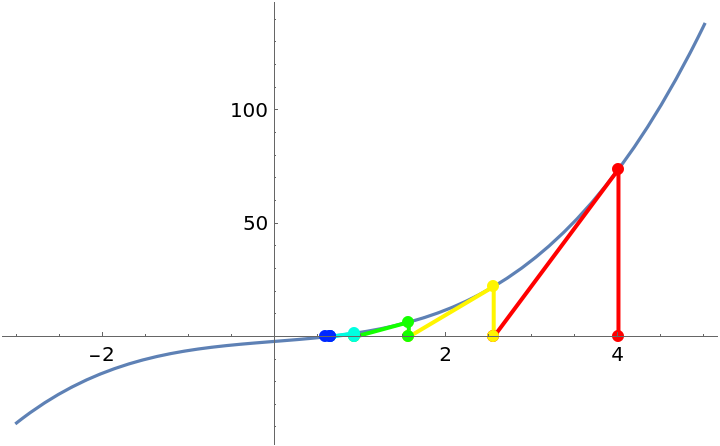 |
Increase the number of iterations:
| In[2]:= |
| Out[2]= | 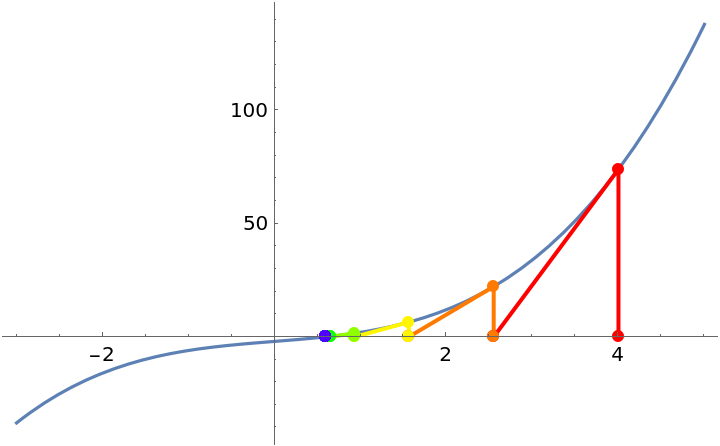 |
Newton’s method can cycle:
| In[3]:= |
| Out[3]= | 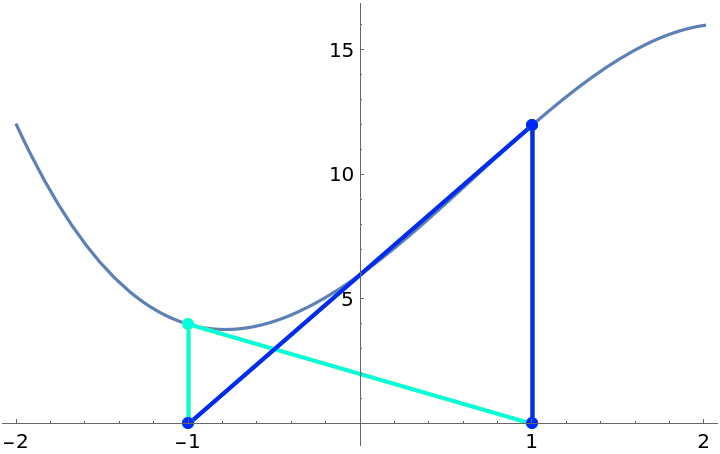 |
Newton’s method may "converge" to a cycle:
| In[4]:= |

| Out[4]= | 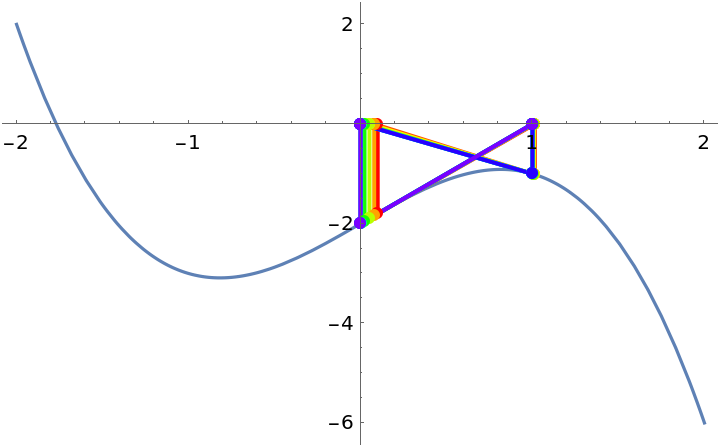 |
Use Surd when necessary:
| In[5]:= |
| In[6]:= |

| Out[6]= | 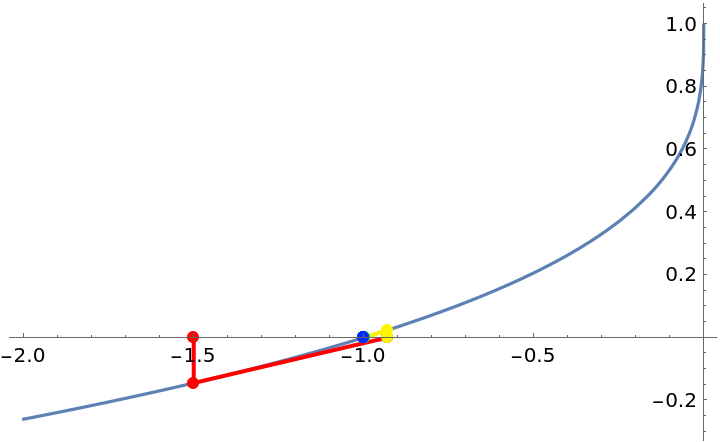 |
Three examples that show that Newton’s method may converge to an unexpected root when it begins or lands near a zero of the derivative:
| In[7]:= |
| Out[7]= | 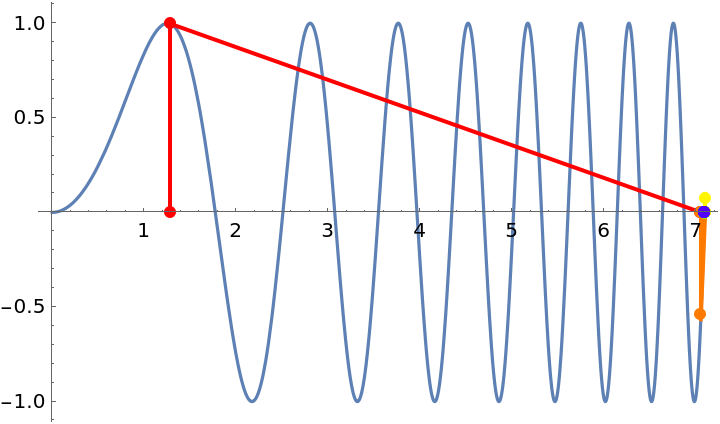 |
| In[8]:= |
| Out[8]= | 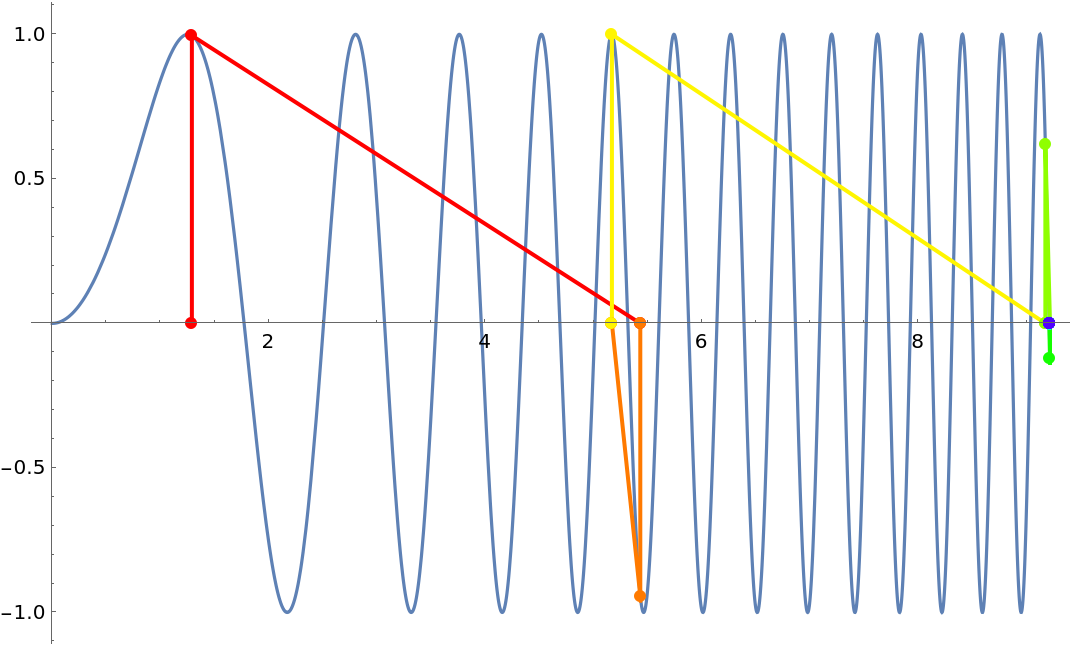 |
| In[9]:= |
| Out[9]= | 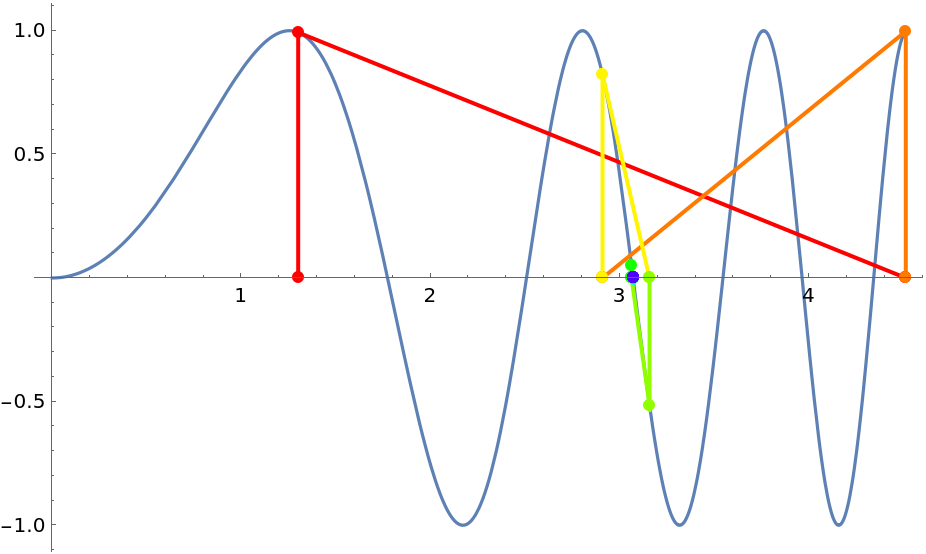 |
This work is licensed under a Creative Commons Attribution 4.0 International License