Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PhiNumberSystem

Source Notebook

Get a list of powers of the golden ratio which sum to a given integer

Contributed by: Wolfram Staff

ResourceFunction["PhiNumberSystem"][n]

gives the list {x1,x2,…,xk} such that ϕx1 + ϕx2 + … + ϕxk = n, where ϕ is GoldenRatio.

Details

The list consists of nonconsecutive distinct integers that may be 0 or negative.
The input must be a nonzero integer.
ResourceFunction["PhiNumberSystem"][n] discards the sign of n.

Examples

Basic Examples (2) 

This gives the golden ratio powers needed to represent 10:

In[1]:=
ResourceFunction["PhiNumberSystem"][10]
Out[1]=

Indeed, the sum of those powers of ϕ is 10:

In[2]:=
Total[GoldenRatio^%]
Out[2]=
In[3]:=
RootReduce[%]
Out[3]=

Scope (2) 

Here are the base-ϕ representations of the first 20 natural numbers:

In[4]:=
Column[ResourceFunction["PhiNumberSystem"][Range[20]]]
Out[4]=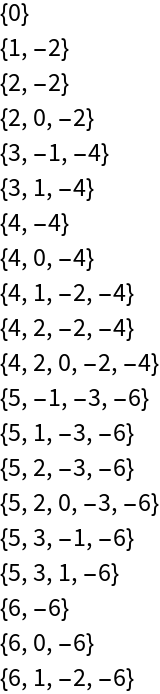

A large example:

In[5]:=
ResourceFunction["PhiNumberSystem"][156347853214]
Out[5]=

Check that the corresponding powers of ϕ sum to the original number:

In[6]:=
Total[GoldenRatio^%] // RootReduce
Out[6]=

Possible Issues (1) 

PhiNumberSystem[n] is left unevaluated for n=0:

In[7]:=
ResourceFunction["PhiNumberSystem"][0]
Out[7]=

Neat Examples (1) 

The sequence of the sums of the lists looks fractal:

In[8]:=
ListLinePlot[Total /@ ResourceFunction["PhiNumberSystem"][Range[800]]]
Out[8]=

Publisher

George Beck

Requirements

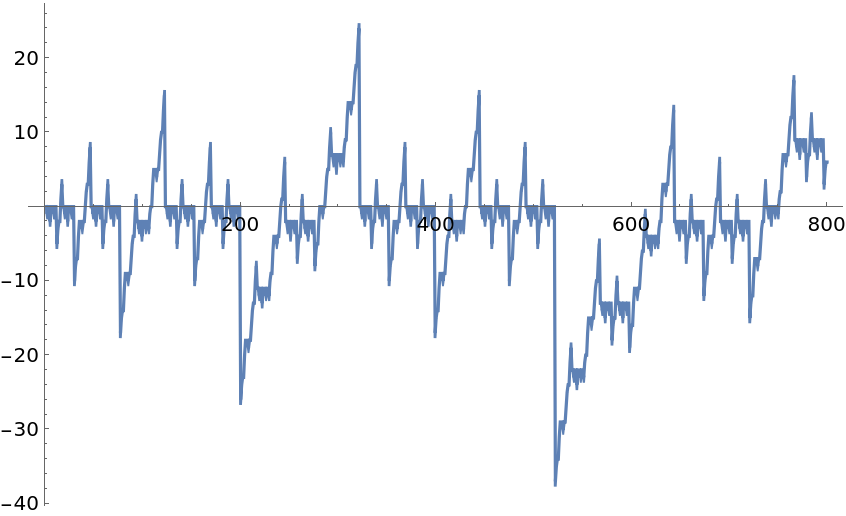Wolfram Language 11.3 (March 2018) or above

Version History

  • 2.0.0 – 25 January 2021
  • 1.0.0 – 26 February 2019

Source Metadata

  • Citation:
    • Bergman G., A Number System with an Irrational Base. Mathematics Magazine, vol. 31, 98-110, 1957.
      DOI: 10.2307/3029218
    • Rousseau, C., The Phi Number System Revisited. Mathematics Magazine, vol. 68, no. 4, 283-284, 1995.
      DOI: 10.1080/0025570X.1995.11996335

Related Resources

License Information