Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a transitive reduction graph for the divisors of a positive integer
ResourceFunction["DivisorHasseDiagram"][n] gives a Hasse diagram based on the divisors of n, represented as a Graph. |
The Hasse diagram for the divisors of 12:
| In[1]:= |
| Out[1]= |  |
| In[2]:= |
| Out[2]= |
The Hasse diagram for a prime number:
| In[3]:= |
| Out[3]= |
For any prime power, DivisorHasseDiagram gives a linear graph where the number of vertices is one more than the exponent of the prime power:
| In[4]:= |
| Out[4]= | 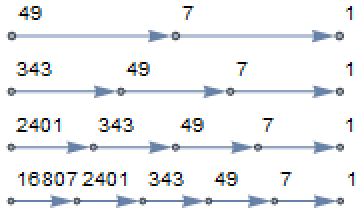 |
The number of edges grows very slowly:
| In[5]:= |
| Out[5]= | 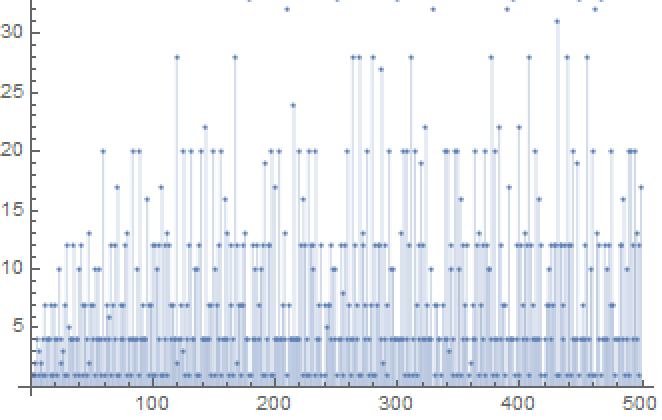 |
720 is an abundant number:
| In[6]:= |
| Out[6]= |
Generate the Hasse diagram:
| In[7]:= |
| Out[7]= | 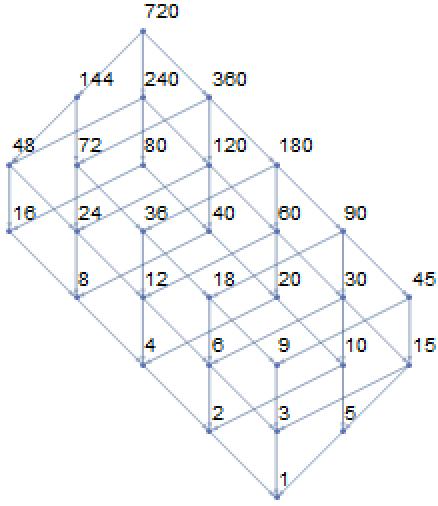 |
2520 is an abundant number:
| In[8]:= |
| Out[8]= |
Generate the Hasse diagram:
| In[9]:= |
| Out[9]= | 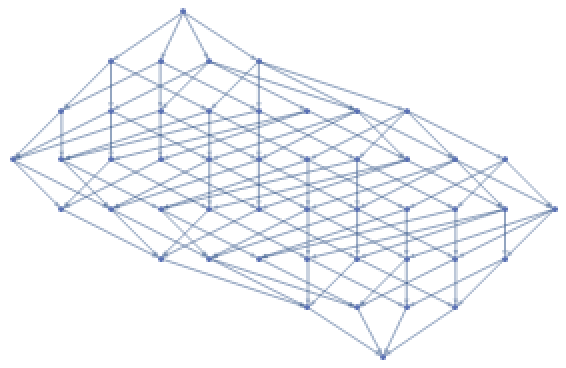 |
21621600 is the only abundant number n that achieves equality in the inequality ![]() , where d(n) is DivisorSigma[0,n] (the inequality was discovered by J.K. Nicolas):
, where d(n) is DivisorSigma[0,n] (the inequality was discovered by J.K. Nicolas):
| In[10]:= |
| Out[10]= | 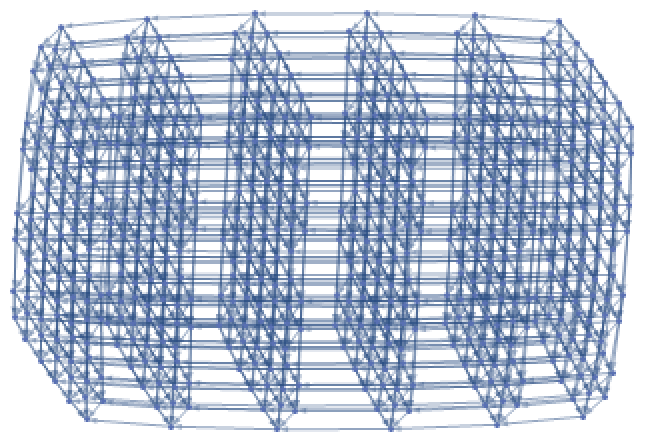 |
This work is licensed under a Creative Commons Attribution 4.0 International License