Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return a pseudorandom unimodular matrix
ResourceFunction["RandomUnimodularMatrix"][n] gives a pseudorandom n×n unimodular matrix. |
| GaussianIntegers | False | whether the matrix returned should have Gaussian integer entries |
| "MaxEntry" | Automatic | bound on the matrix elements |
| MaxIterations | Automatic | maximum number of iterations to use |
Generate a random 5×5 unimodular matrix:
| In[1]:= |
| Out[1]= |  |
Its inverse has integer entries:
| In[2]:= |
| Out[2]= | 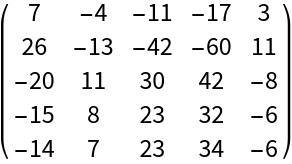 |
A medium-sized unimodular matrix:
| In[3]:= |
| Out[3]= |  |
Generate a unimodular matrix with Gaussian integer entries:
| In[4]:= |
| Out[4]= | 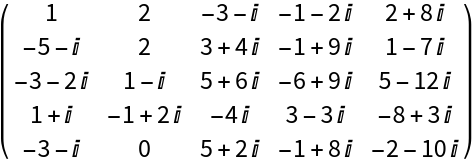 |
Its inverse has Gaussian integer entries:
| In[5]:= |
| Out[5]= | 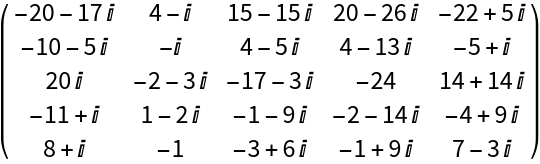 |
Generate a unimodular matrix with elements between -2 and 2:
| In[6]:= |
| Out[6]= |  |
Change the number of iterations needed to generate the matrix:
| In[7]:= |
| Out[7]= |  |
Generate an integer matrix with integer eigenvalues:
| In[8]:= | ![n = 5;
u = ResourceFunction["RandomUnimodularMatrix"][n];
MatrixForm[
mat = Inverse[u] . DiagonalMatrix[RandomInteger[{-9, 9}, n]] . u]](https://www.wolframcloud.com/obj/resourcesystem/images/37c/37c49bdc-640c-4a5b-a533-1c0ecc173313/734c530570cd394c.png) |
| Out[8]= | 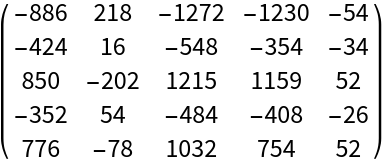 |
Show its eigenvalues and eigenvectors:
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License