Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CircularPrimeQ

Source Notebook

Test whether an integer is a circular prime

Contributed by: Phileas Dazeley-Gaist

ResourceFunction["CircularPrimeQ"][int]

gives True if int is a base-10 circular prime, and False otherwise.

ResourceFunction["CircularPrimeQ"][int,b]

gives True if int is a base-b circular prime, and False otherwise.

Details

ResourceFunction["CircularPrimeQ"][int] returns False unless int is manifestly a base-10 circular prime (i.e. if it remains prime after any cyclic permutation of its base-10 digits).
ResourceFunction["CircularPrimeQ"][int,b] returns False unless int is manifestly a base-b circular prime (i.e. if it remains prime after any cyclic permutation of its base-b digits).
In base 2, Mersenne primes are circular. The longest known base ten circular prime is 8177207 ones in row, a so called repunit prime.

Examples

Basic Examples (2) 

CircularPrimeQ tests whether an integer is a circular prime:

In[1]:=
ResourceFunction["CircularPrimeQ"][11939]
Out[1]=

Test CircularPrimeQ on a non-circular prime:

In[2]:=
ResourceFunction["CircularPrimeQ"][29]
Out[2]=

Scope (2) 

Compute a list of base-10 circular primes in the first 100000 primes:

In[3]:=
cps = Select[Map[Prime, Range[100000]], ResourceFunction[ "CircularPrimeQ"]]
Out[3]=

Make a number line plot of the resulting list:

In[4]:=
NumberLinePlot[cps]
Out[4]=

Applications (2) 

Count circular and non-circular primes in the first 10000 primes:

In[5]:=
Counts[ResourceFunction["CircularPrimeQ"]@*Prime /@ Range[10000]]
Out[5]=

Make a Dataset of the base-b circular primes among the first 10000 primes:

In[6]:=
circularPrimesDataset = Dataset[AssociationThread[Range[2, 10], With[{primes = Range[10000]}, Table[ Select[Map[Prime, primes], ResourceFunction["CircularPrimeQ"][#, base] &], {base, 2, 10, 1}]]]]
Out[6]=

Plot the result using NumberLinePlot:

In[7]:=
NumberLinePlot[circularPrimesDataset]
Out[7]=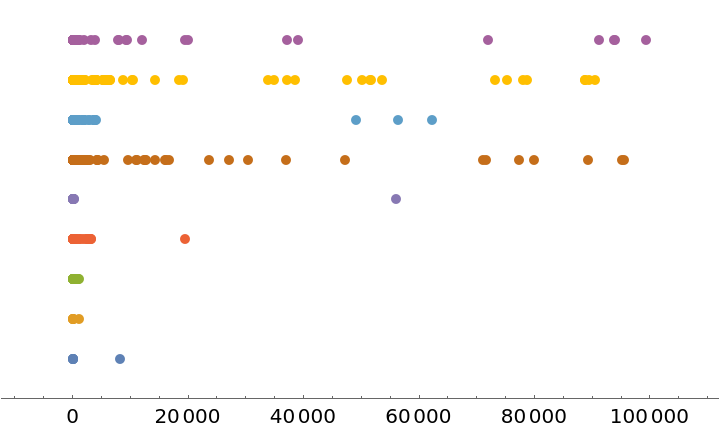

Find out how many of the first 10000 primes are circular primes in bases 2 through 10:

In[8]:=
Normal@circularPrimesDataset[All, Length]
Out[8]=

Find out which of the circular primes in the first 10000 primes are circular in the most bases:

In[9]:=
Dataset[ReverseSort[ Counts[ReverseSort[Flatten[Normal[Values[circularPrimesDataset]]]]]], MaxItems -> 5]
Out[9]=

Publisher

Phileas Dazeley-Gaist

Requirements

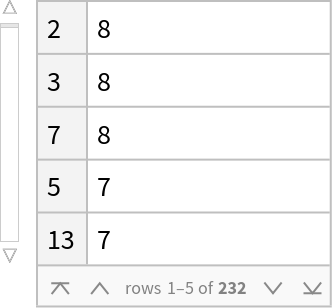Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 02 October 2024

Source Metadata

Related Resources

License Information