Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Schur polynomial corresponding to an integer partition
ResourceFunction["SchurS"][p,{x1,…,xn}] gives the Schur polynomial sp(x1,…,xn) corresponding to the integer partition p in the variables x1,…,xn. |
A Schur polynomial in two variables:
| In[1]:= |
| Out[1]= |
Generate all partitions of 8 into at most 3 integers:
| In[2]:= |
| Out[2]= |
Generate all Schur polynomials in three variables of degree 8:
| In[3]:= |
| Out[3]= |  |
Count the number of semi-standard Young tableaux of shape (4 2 1 1), with entries taken from the numbers 1 to 4:
| In[4]:= |
| Out[4]= |
Verify Jacobi's bialternant formula for the Schur polynomial:
| In[5]:= | ![p = {4, 3, 1, 1}; vars = {x, y, z, w};
ResourceFunction["SchurS"][p, vars] == PolynomialReduce[
Det[Outer[Power, vars, PadRight[p, Length[vars]] + Range[Length[vars] - 1, 0, -1]]], Det[VandermondeMatrix[vars]], vars][[1, 1]] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/369/3698e252-946d-4a75-a22c-56145157e2d9/0ad436b9a2ce2883.png) |
| Out[6]= |
Generate all monomial symmetric polynomials of degree 5:
| In[7]:= |
| Out[8]= | 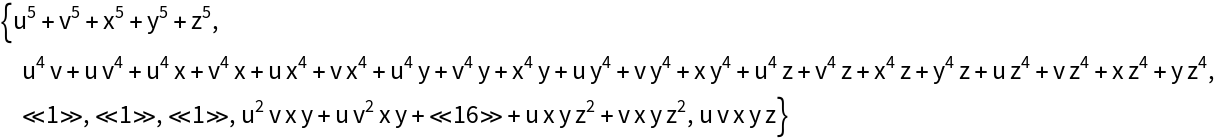 |
Generate the Kostka numbers as the coefficients that arise when the Schur polynomial is expanded in the monomial symmetric basis:
| In[9]:= |
| Out[9]= |
The Littlewood-Richardson rule states that the product of two Schur polynomials can be expressed as a linear combination of Schur polynomials with integer coefficients. Generate the product from the original example by Littlewood and Richardson:
| In[10]:= | ![vars = {\[FormalX][1], \[FormalX][2], \[FormalX][3], \[FormalX][
4], \[FormalX][5], \[FormalX][6]};
p1 = {4, 3, 1}; p2 = {2, 2, 1};
Short[prod = ResourceFunction["SchurS"][p1, vars] ResourceFunction["SchurS"][p2, vars]]](https://www.wolframcloud.com/obj/resourcesystem/images/369/3698e252-946d-4a75-a22c-56145157e2d9/07ff98fb0594091e.png) |
| Out[11]= |
Use PolynomialReduce to find the coefficients for the Schur polynomial terms of the product (this might take a while to evaluate):
| In[12]:= | ![pList = IntegerPartitions[Total[p1] + Total[p2], Length[vars]];
basis = Table[ResourceFunction["SchurS"][p, vars], {p, pList}];
AbsoluteTiming[{coef, rem} = PolynomialReduce[prod, basis, vars]]](https://www.wolframcloud.com/obj/resourcesystem/images/369/3698e252-946d-4a75-a22c-56145157e2d9/01046c85cba0923c.png) |
| Out[13]= |
Show the mapping between the nonzero coefficients and their corresponding partitions:
| In[14]:= |
| Out[14]= |  |
Reconstruct the original polynomial:
| In[15]:= |
| Out[15]= |
PolynomialReduce can be used to find the coefficients for the expansion of any symmetric polynomial in the Schur basis:
| In[16]:= | ![poly = x^4 + y^4 + z^4;
basis = Table[
ResourceFunction["SchurS"][p, {x, y, z}], {p, IntegerPartitions[4, 3]}];
coef = First[PolynomialReduce[poly, basis, {x, y, z}]]](https://www.wolframcloud.com/obj/resourcesystem/images/369/3698e252-946d-4a75-a22c-56145157e2d9/409edc4ec9530e49.png) |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License