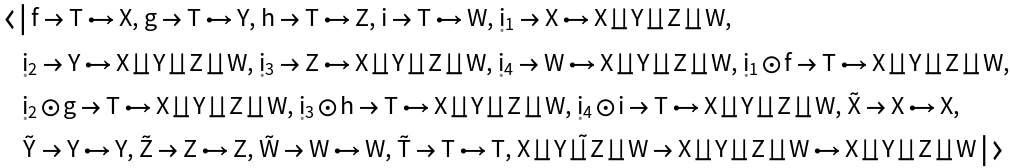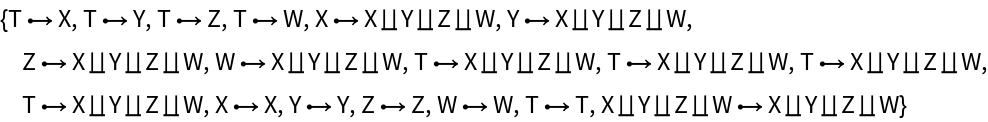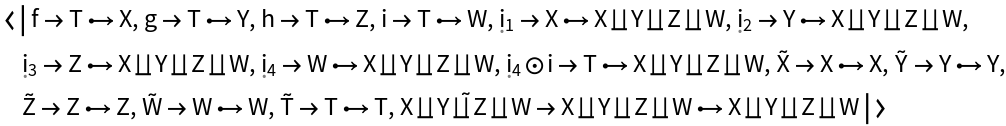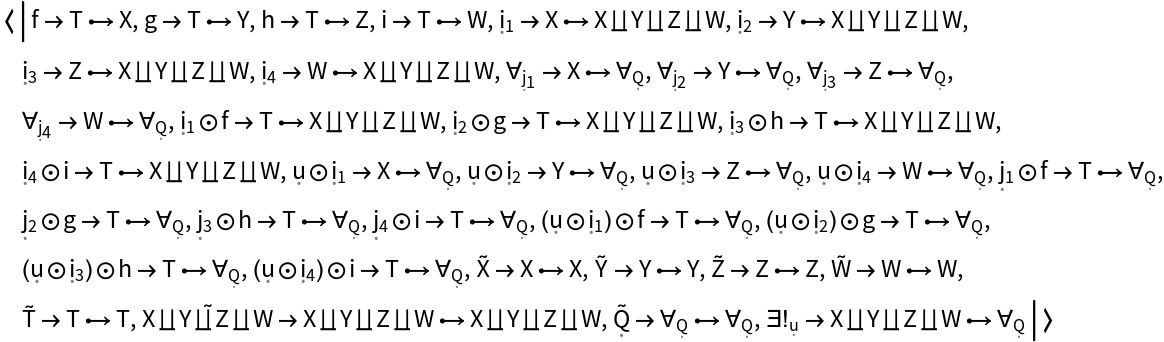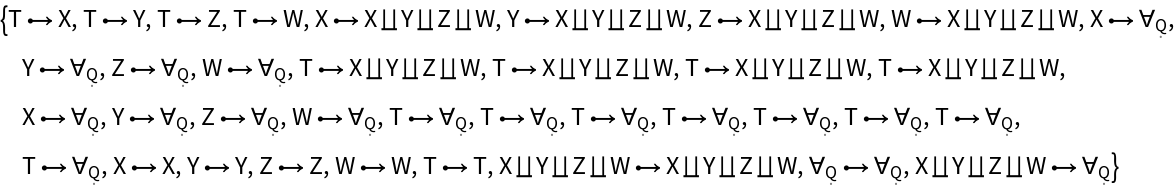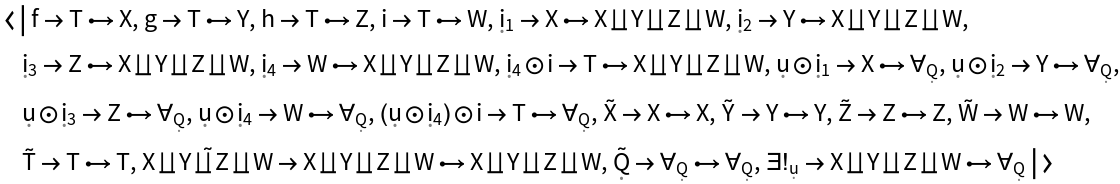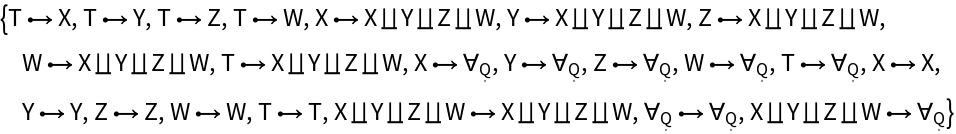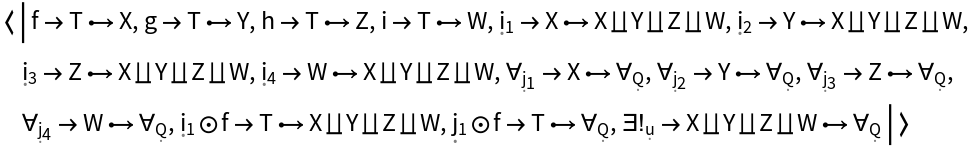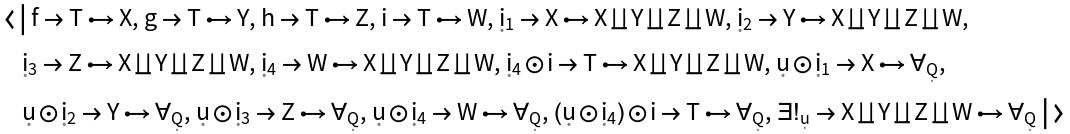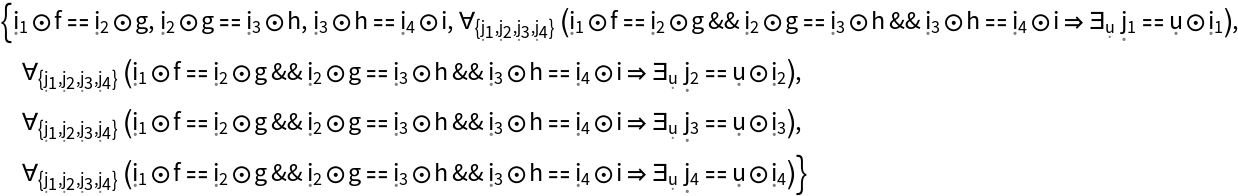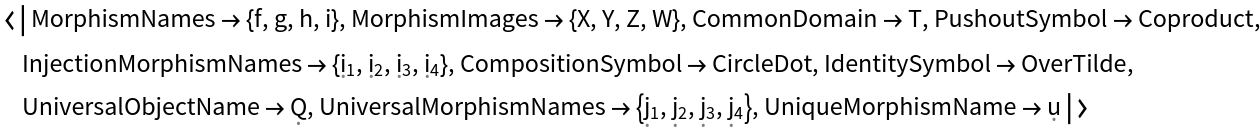Basic Examples (3)
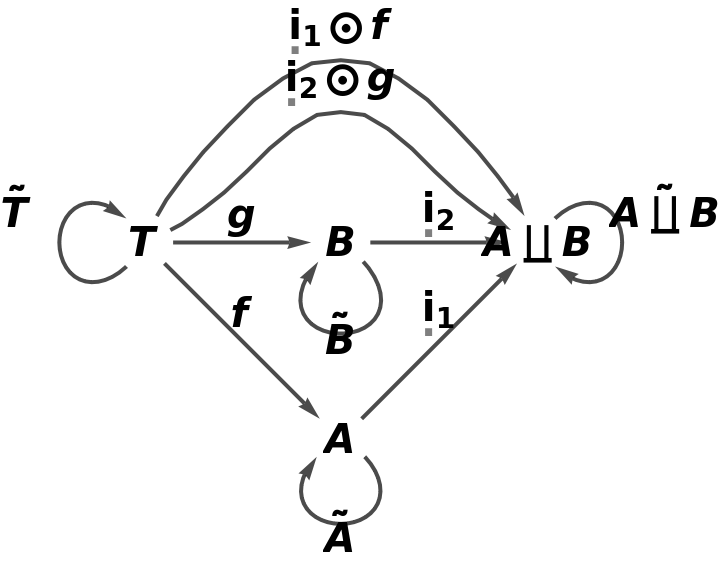
Construct a simple abstract pushout of morphisms f and g from a common object T to objects A and B:
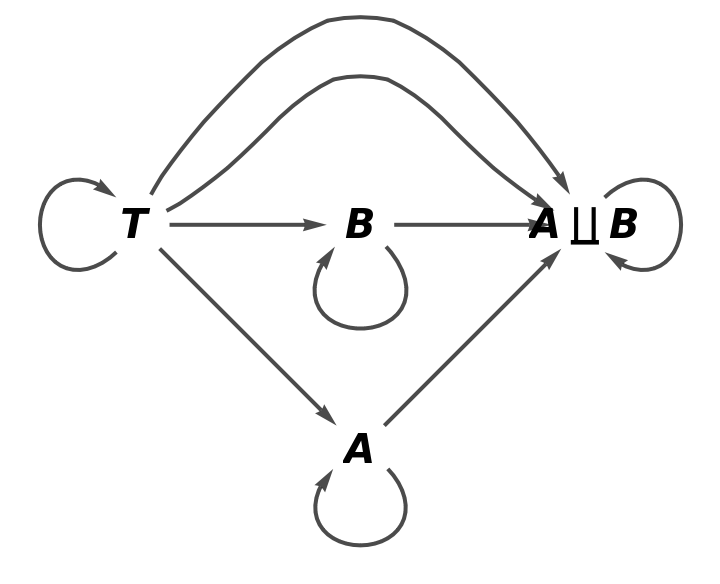
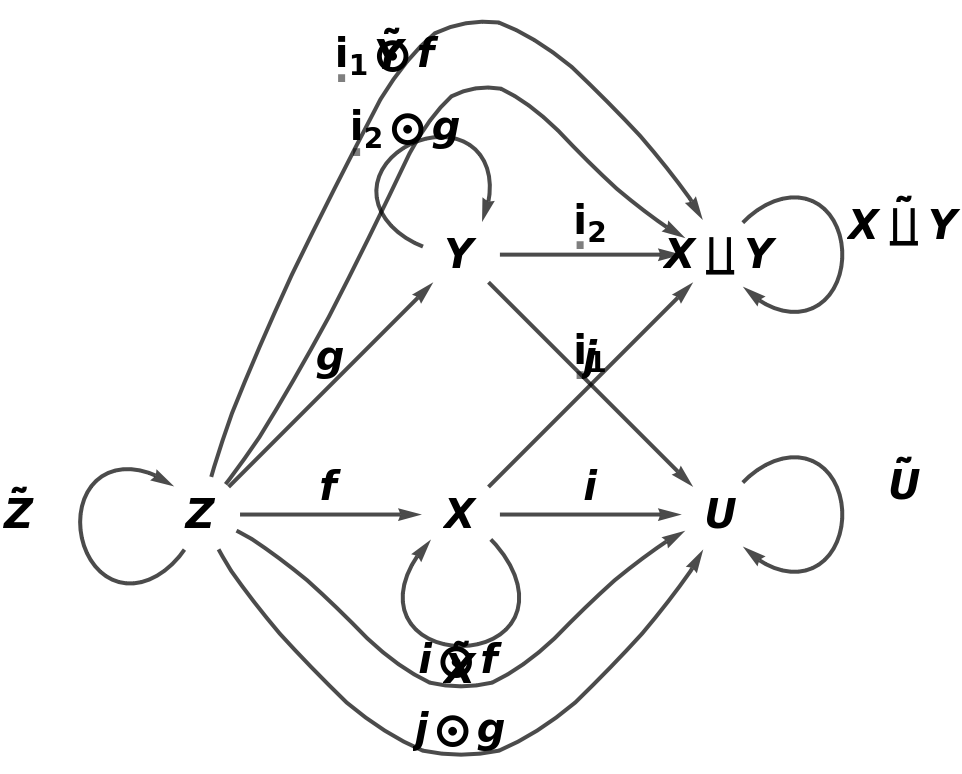
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
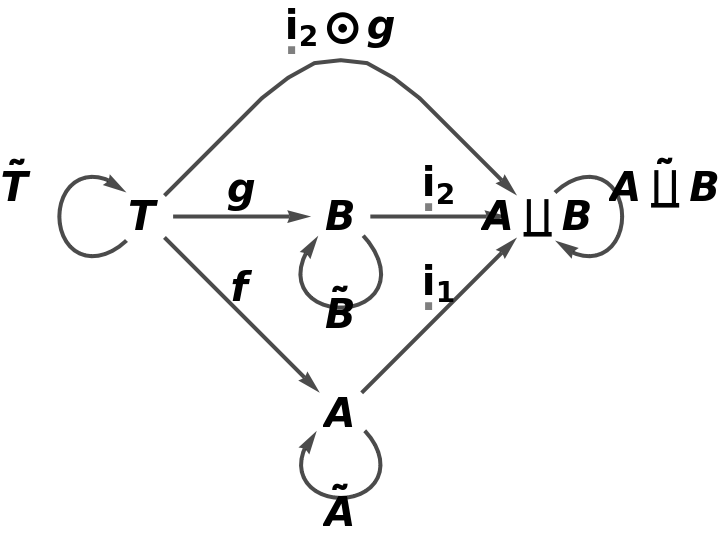
Show the reduced directed graph, with all equivalences between morphisms imposed and with labels on the morphisms, illustrating that the pushout diagram commutes:
Show the reduced directed graph without labels on the morphisms:
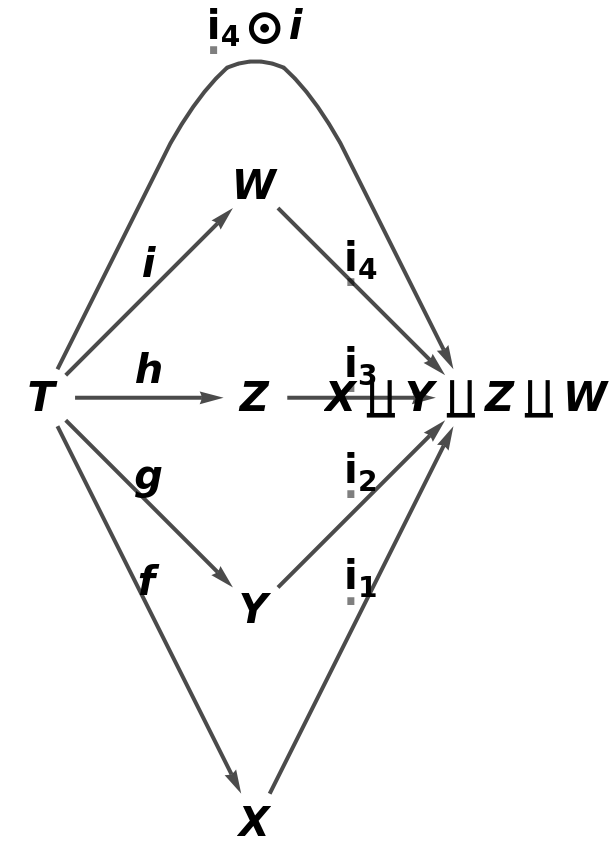
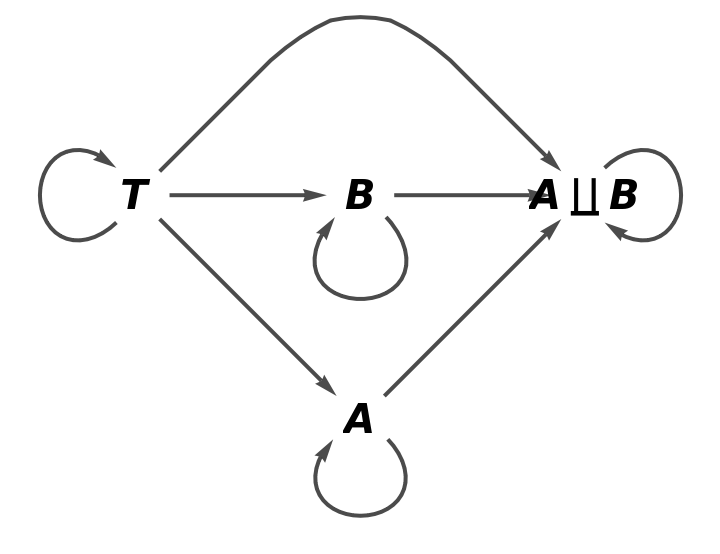
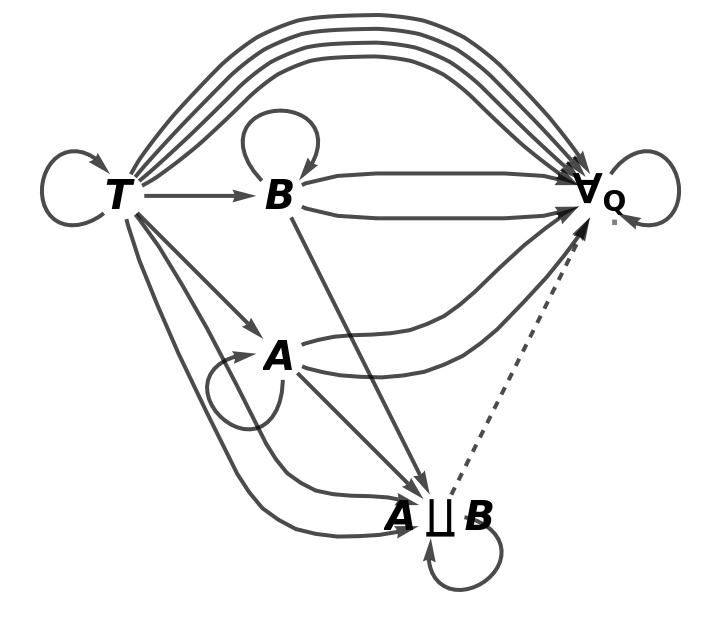
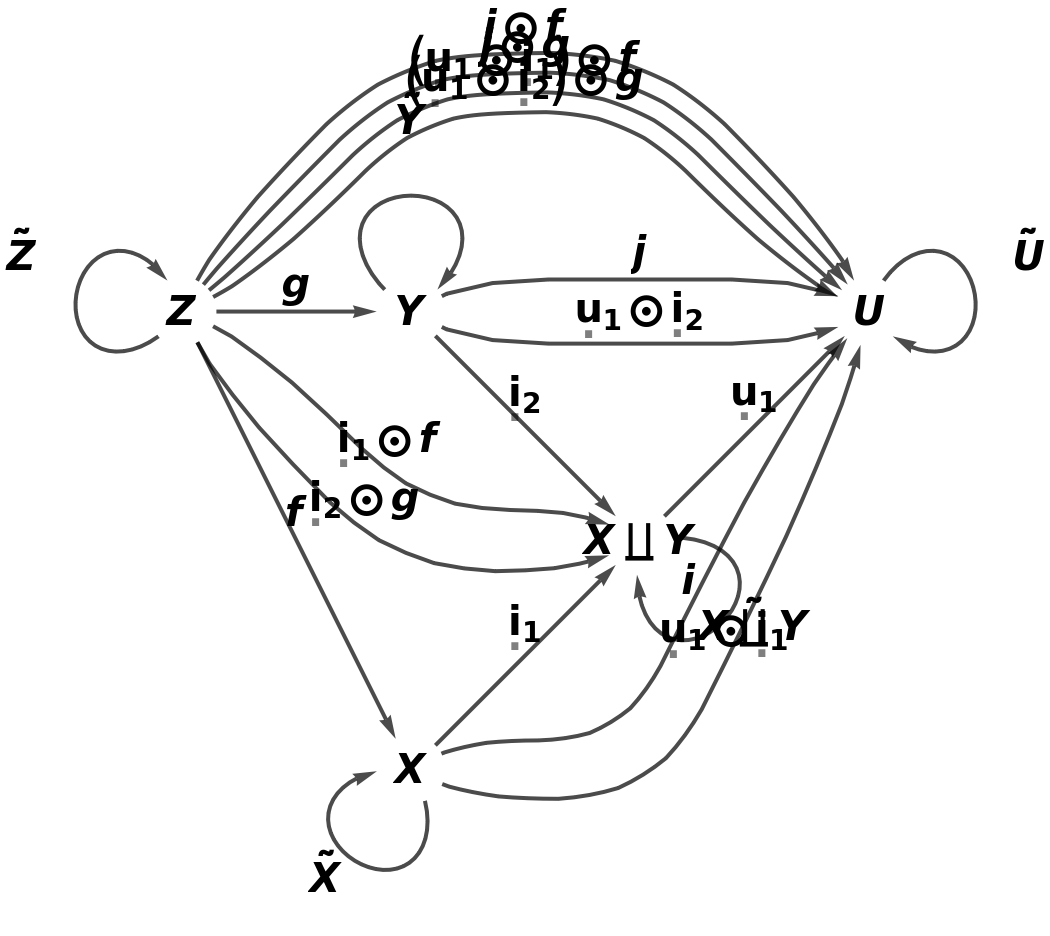
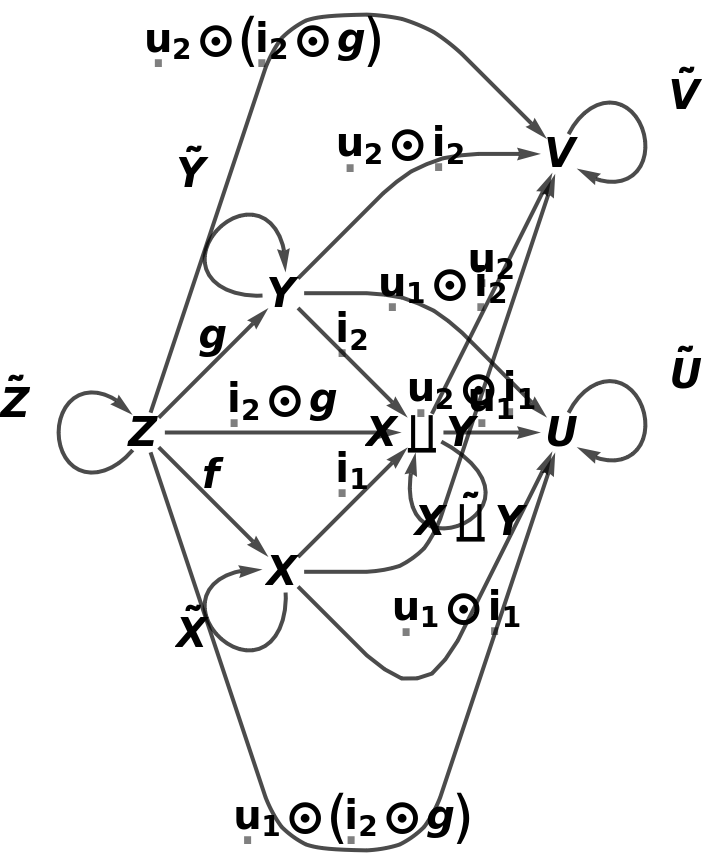
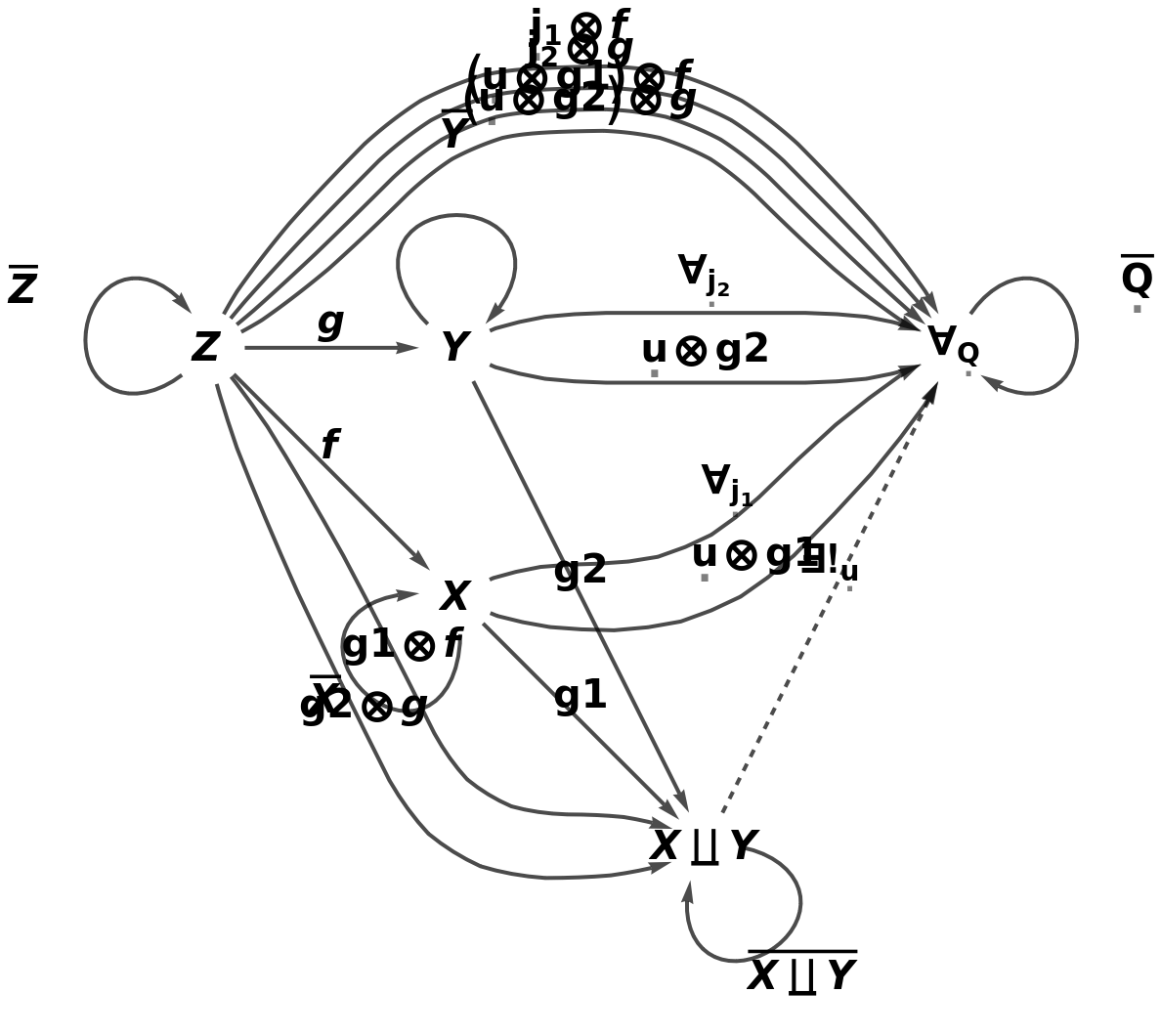
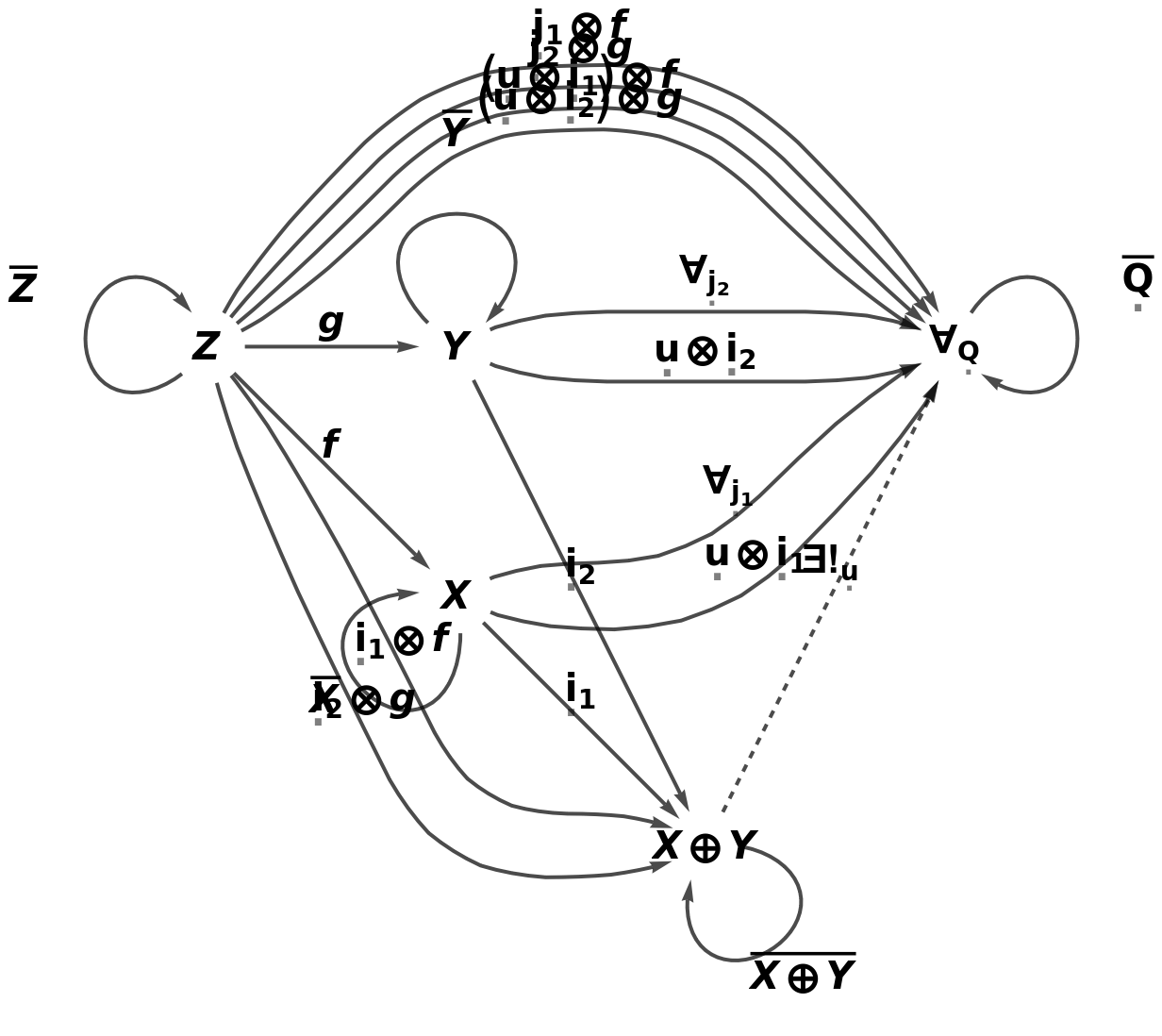
Show the full directed graph characterizing the universal property, with labels on the morphisms:
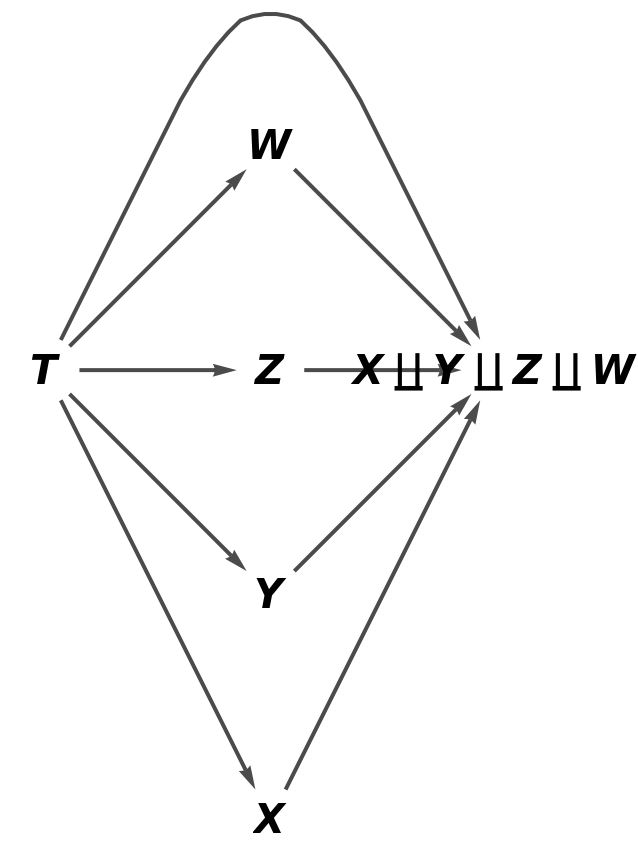
Show the full directed graph characterizing the universal property, without labels on the morphisms:
Show the Association of morphisms:
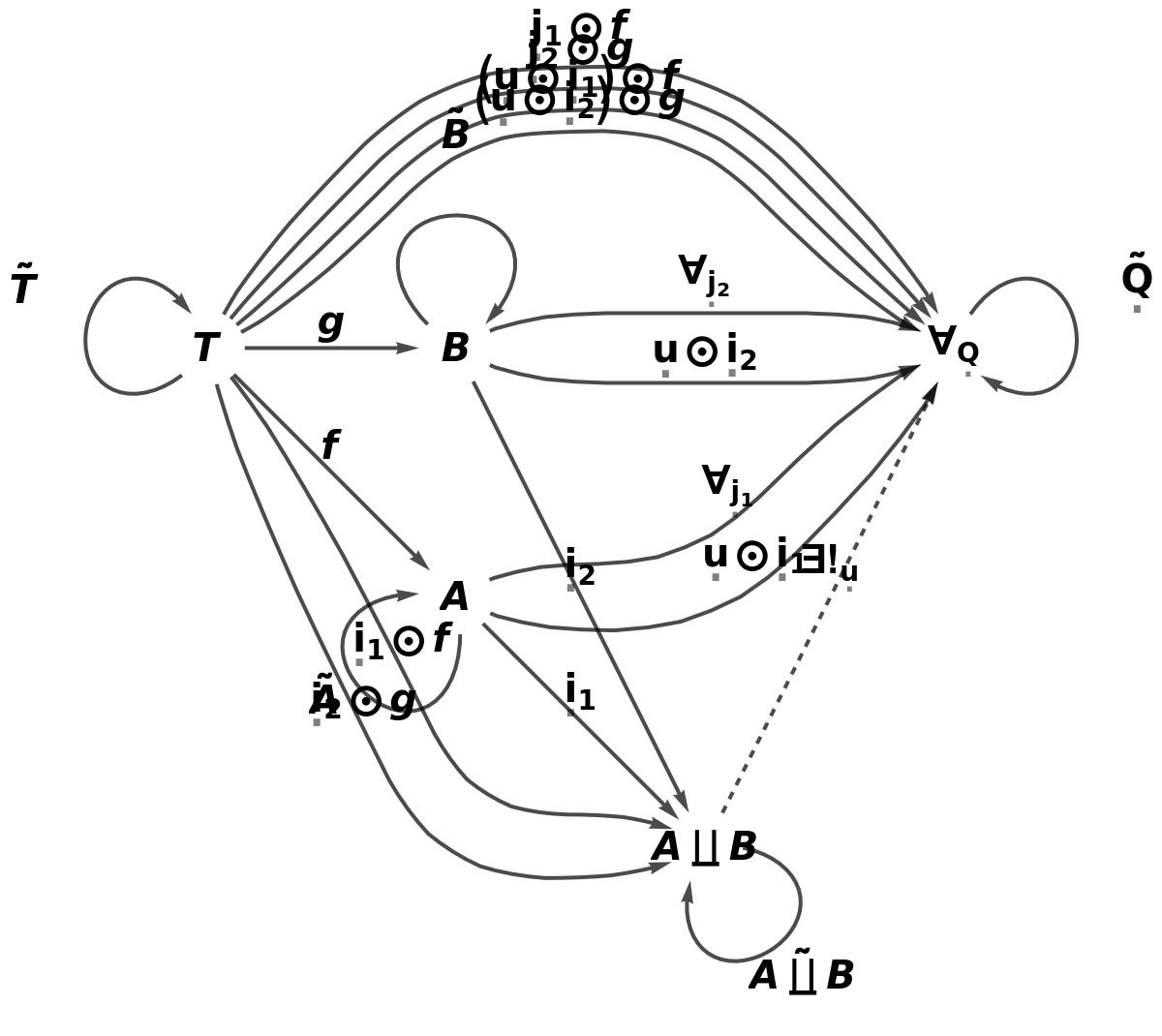
Show the Association of (quantified) morphisms characterizing the universal property:
Show the list of directed edges characterizing the universal property:
Show the list of equations required to force the pushout diagram to commute:
Show the list of equations required to force the pushout diagram to commute, plus the equations characterizing the universal property:
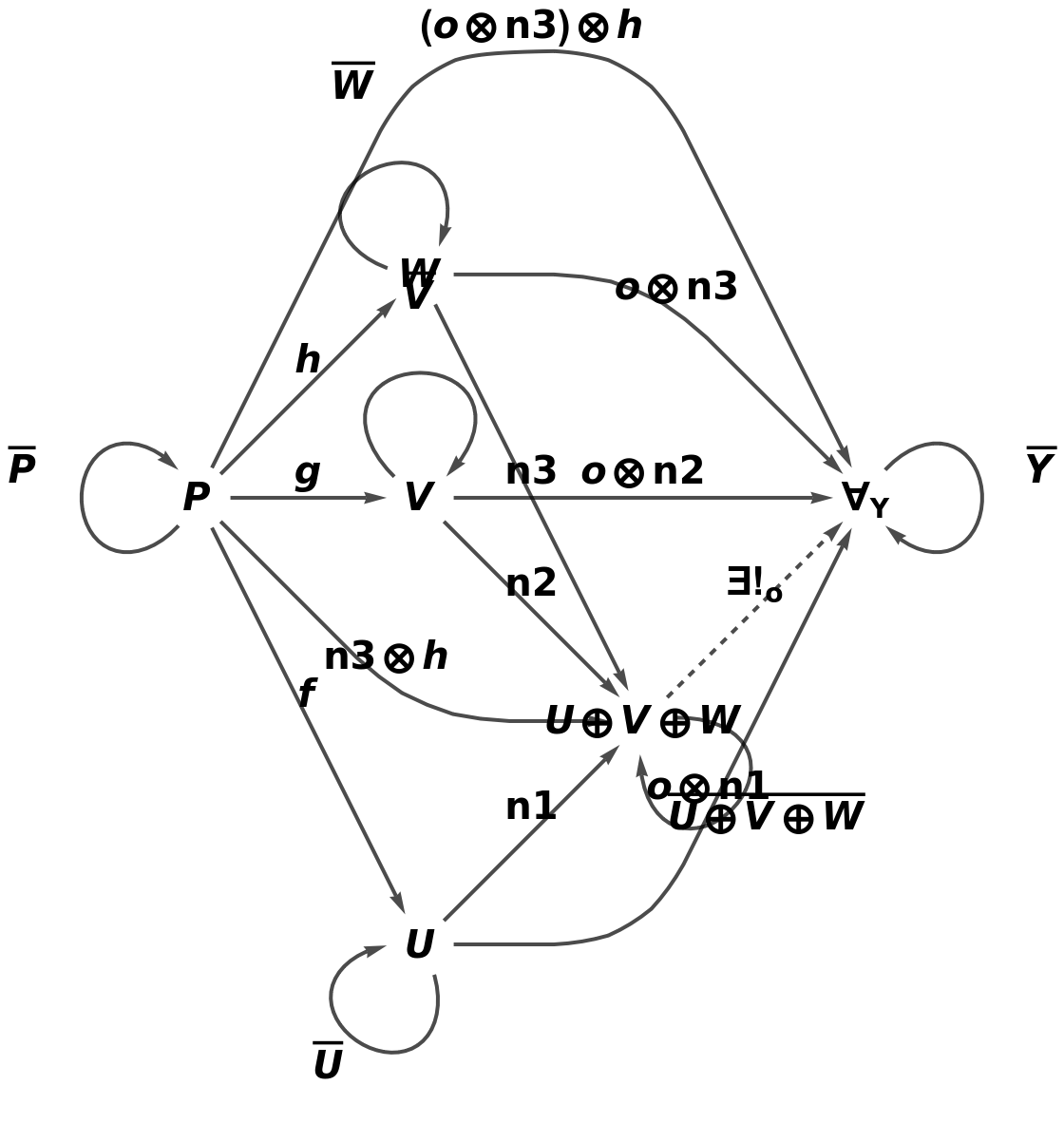
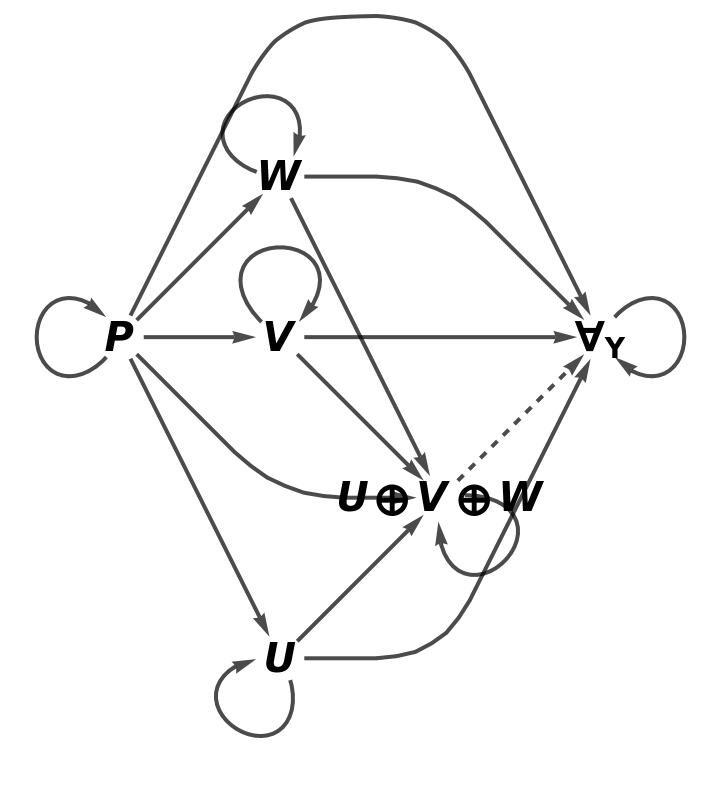
Construct an abstract (wide) pushout of morphisms f, g and h from a common object P to objects U, V and W, but with pushout symbol ⊕, injection morphisms n1, n2 and n3, composition and identity symbols ⊗ and ─, and with a universal property characterized by universal object Y, universal morphisms o1, o2 and o3, and unique morphism o:
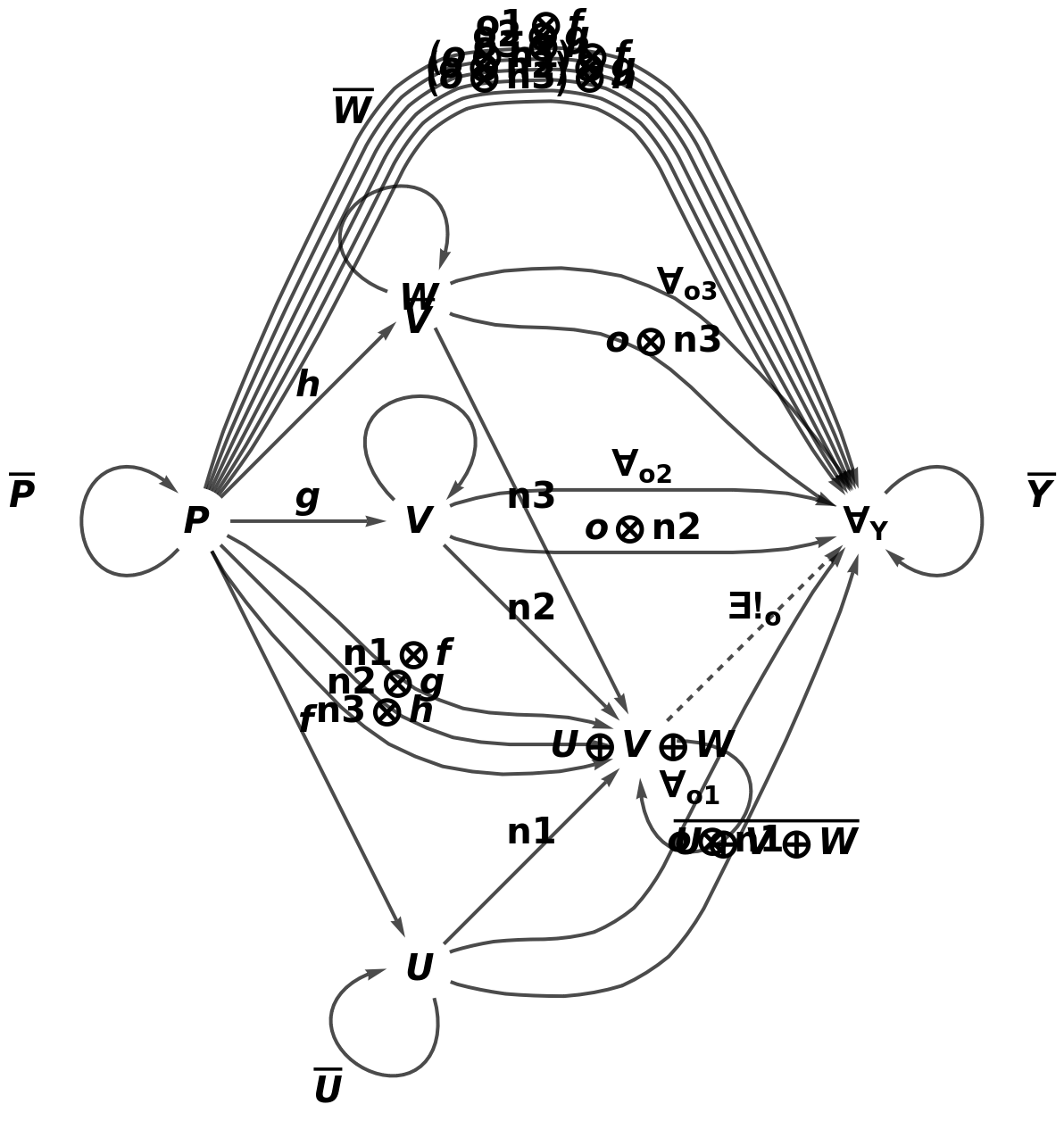
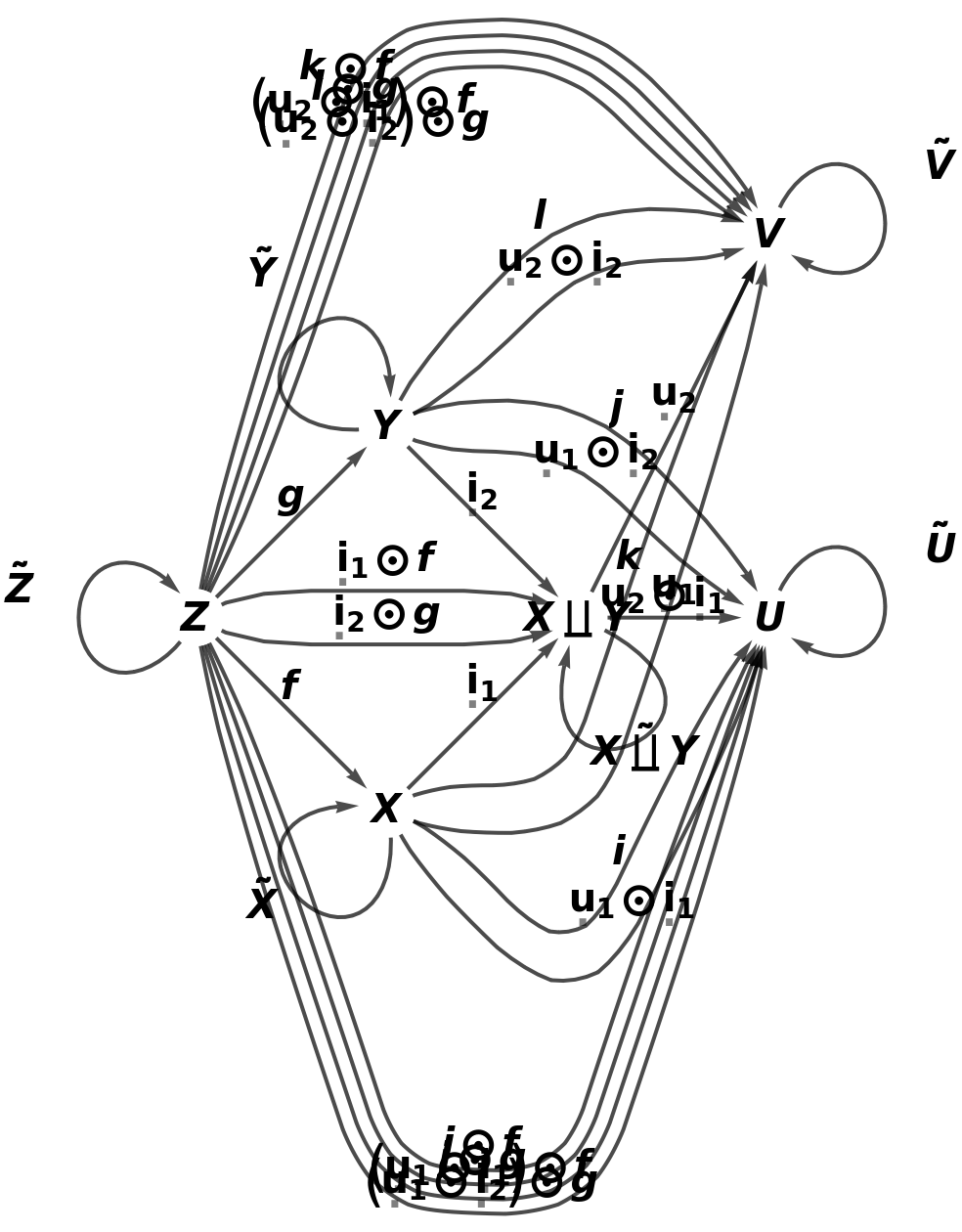
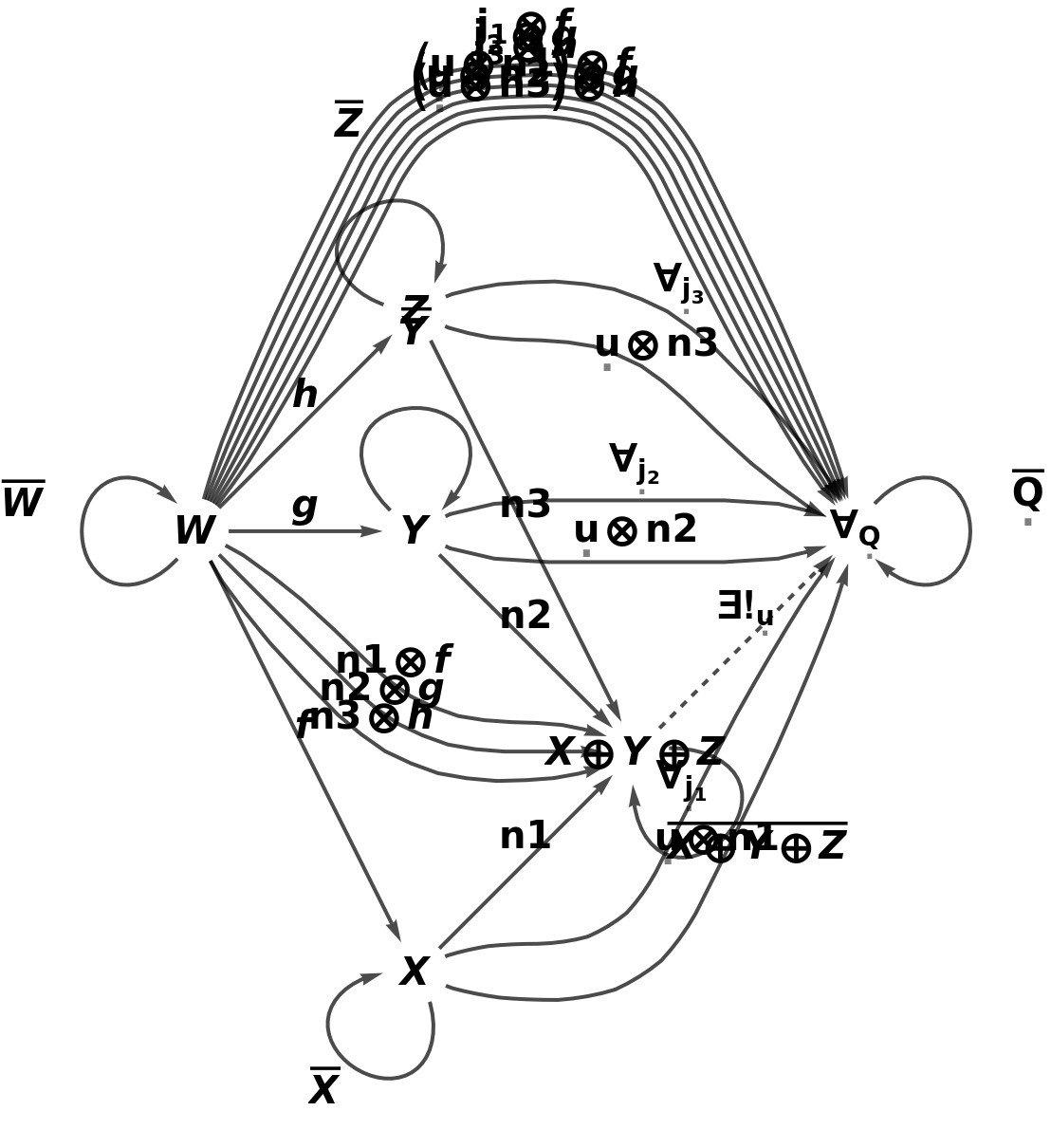
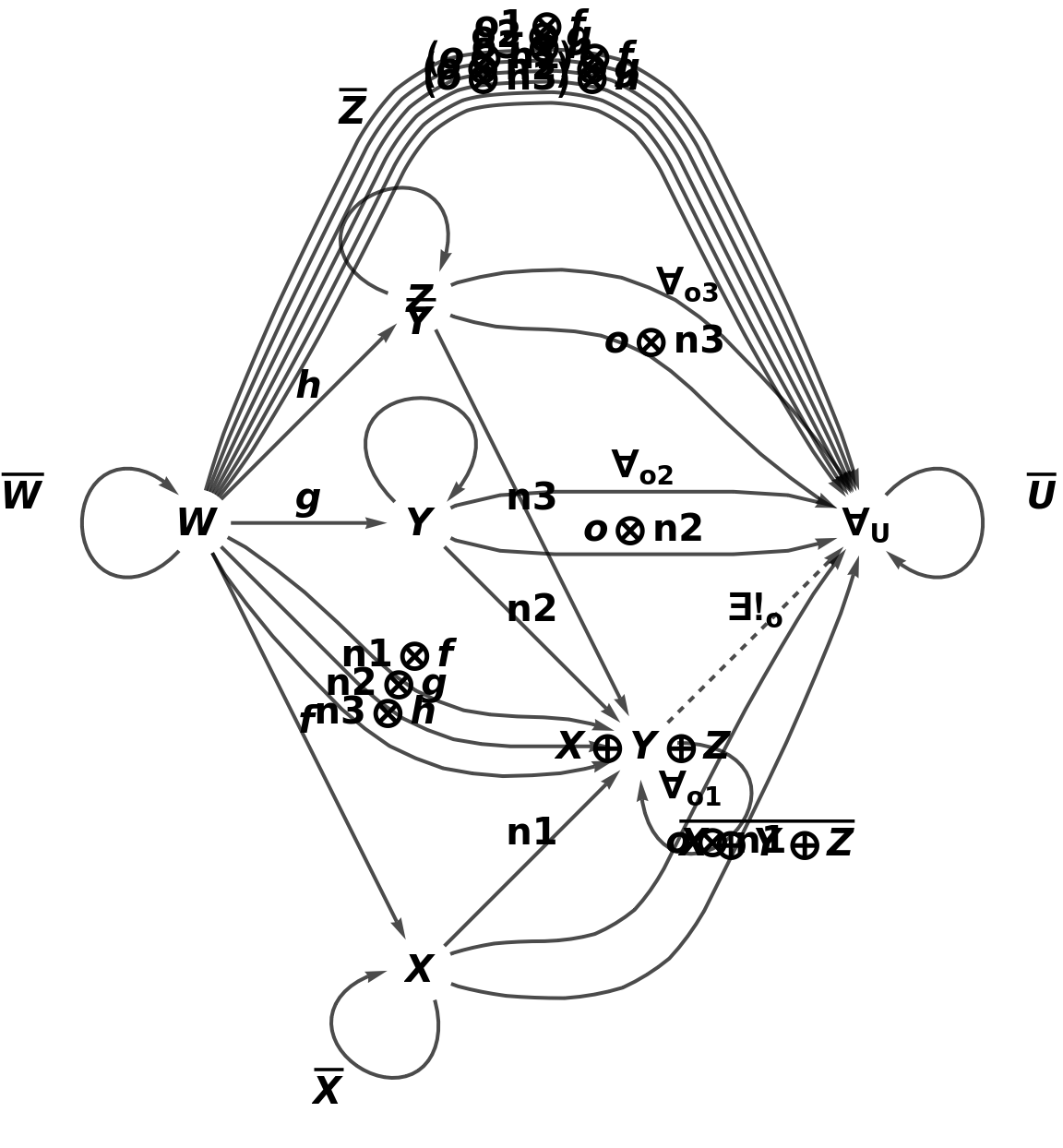
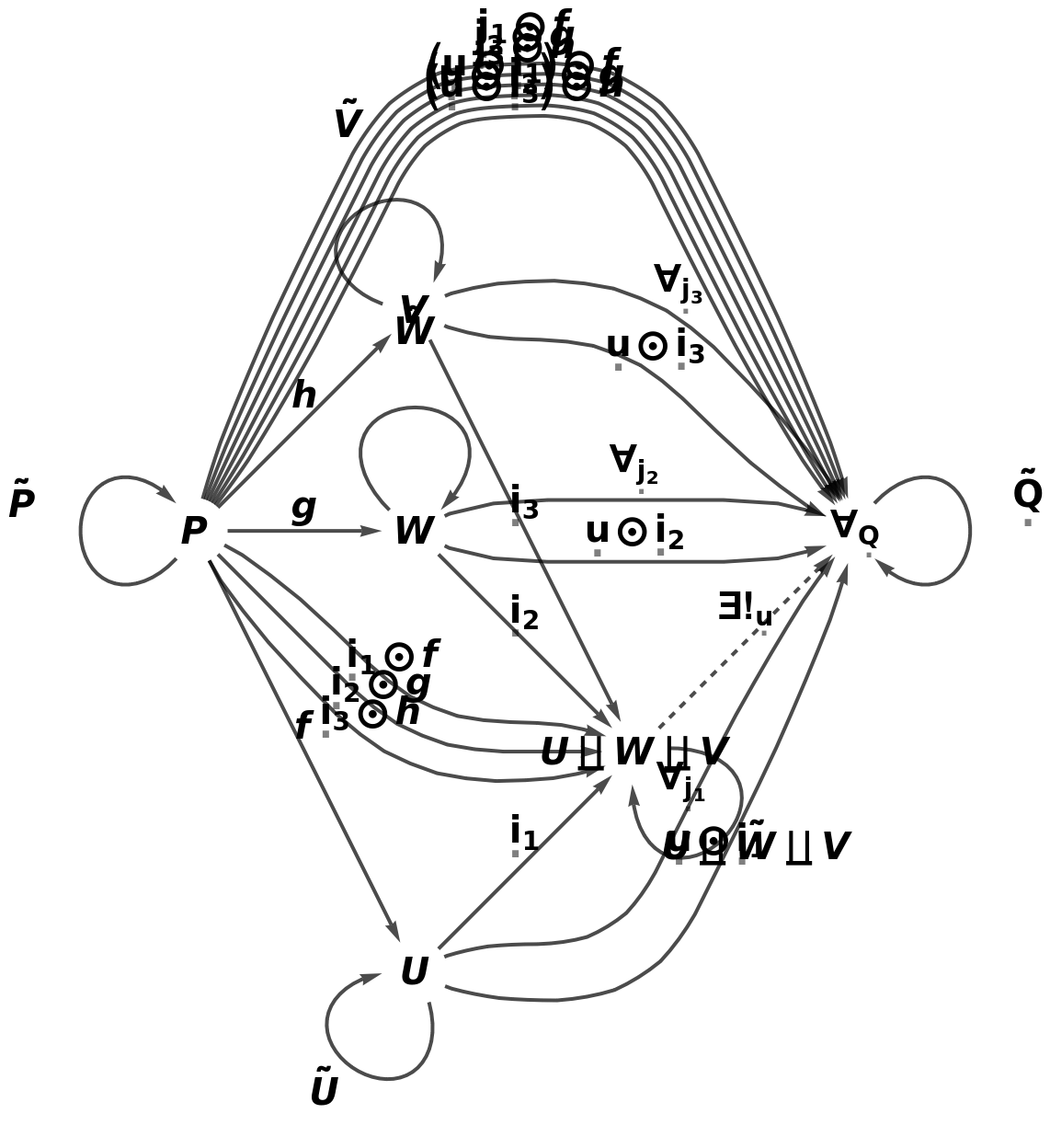
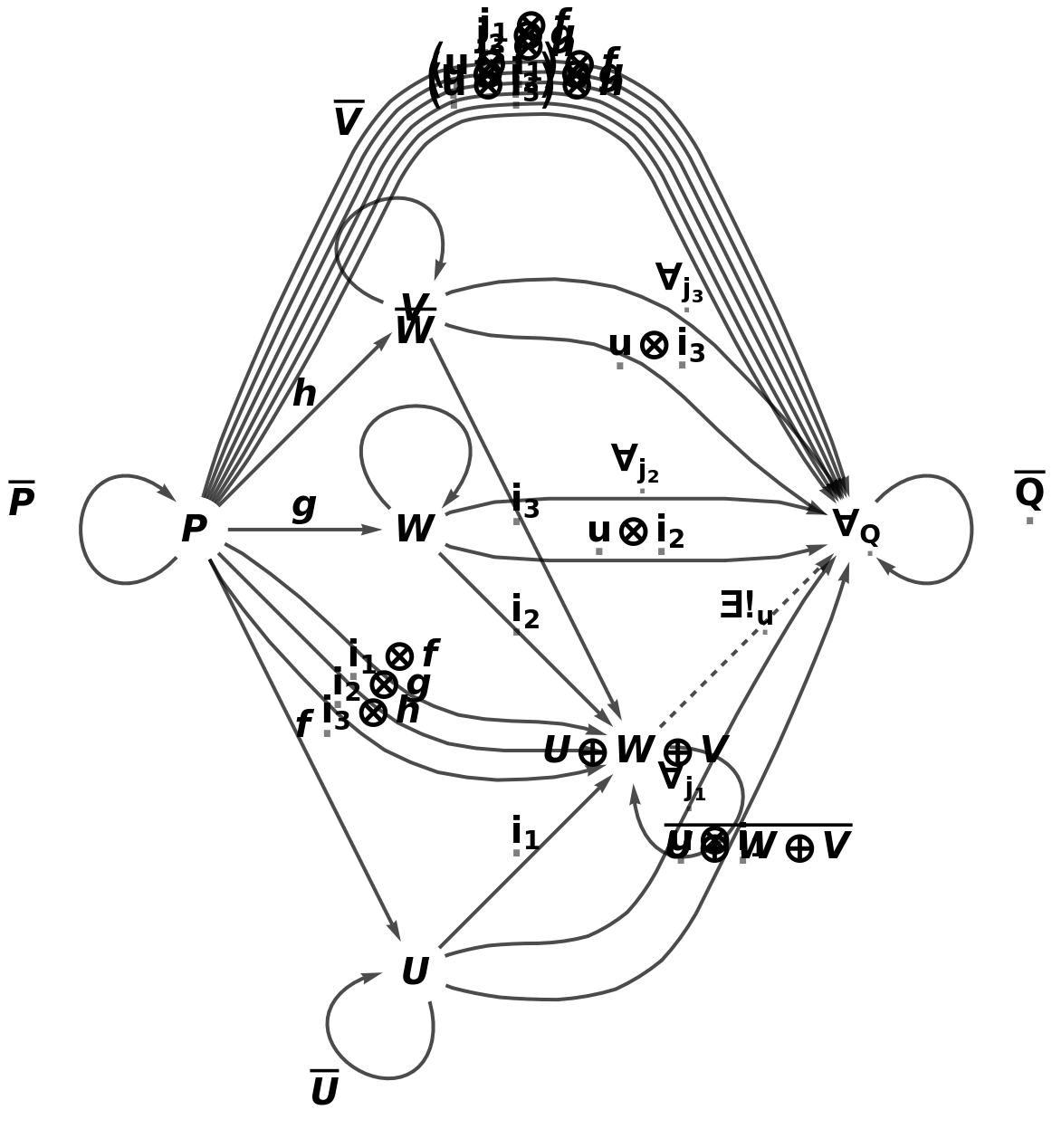
Show the full directed graph characterizing the universal property, with labels on the morphisms:
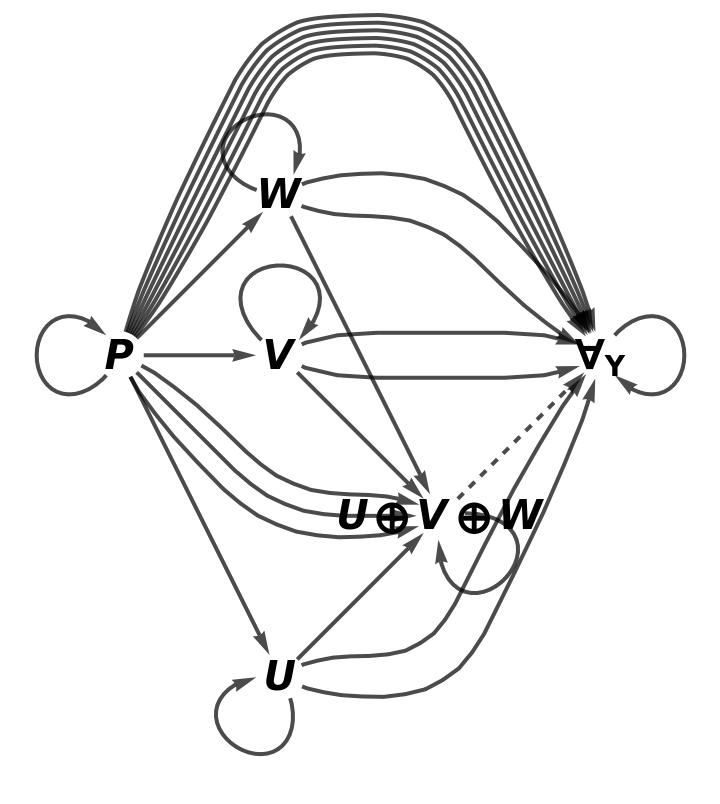
Show the full directed graph characterizing the universal property, without labels on the morphisms:
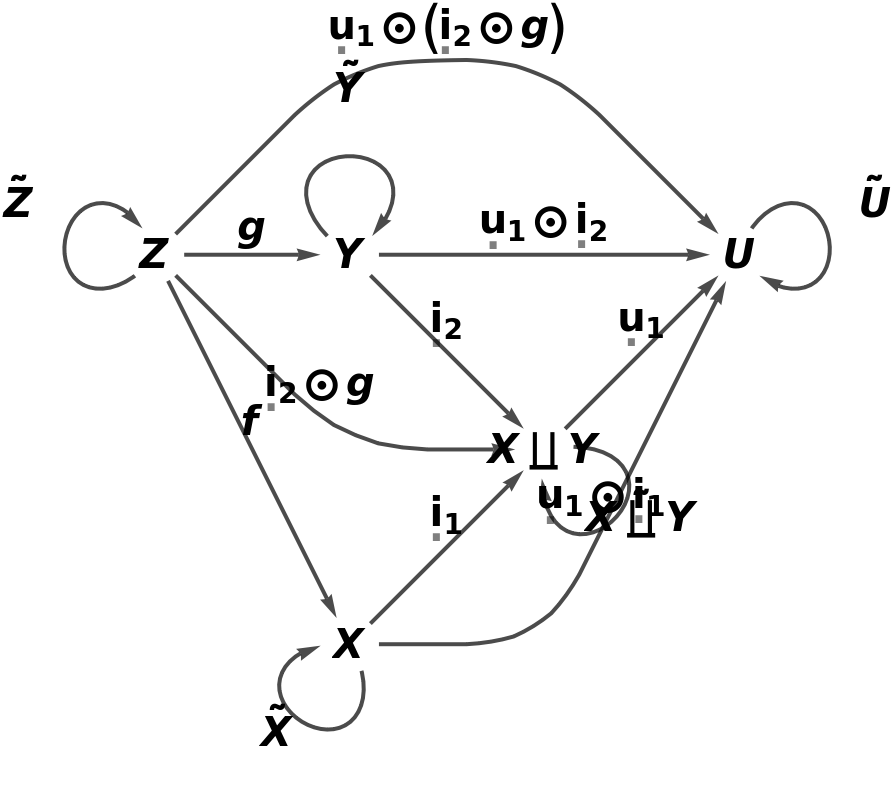
Show the reduced directed graph characterizing the universal property, with all equivalences between morphisms imposed and with labels on the morphisms:
Show the reduced directed graph characterizing the universal property, without labels on the morphisms:
Show the Association of morphisms, with all equivalences between morphisms imposed:
Show the Association of morphisms characterizing the universal property, with all equivalences between morphisms imposed:
Show the list of equations required to force the (wide) pushout diagram to commute, plus the equations characterizing the universal property:
Show the association form of the abstract (wide) pushout:
Construct an abstract pushout of morphisms f and g from a common object Z to objects X and Y:
Construct an abstract category consisting of f and g, plus morphisms from X and Y to some common object U:
Embed the abstract pushout into the abstract category:
Note that, since the commutativity condition on morphisms i and j is not satisfied, the universal property is not invoked:
Force the commutativity condition on morphisms i and j to be satisfied:
Embed the abstract pushout into the new abstract category (in such a way that the universal property is satisfied):
Validate that the universal property is indeed satisfied:
Construct a more complicated abstract category consisting of additional morphisms from X and Y to some further common object V (such that these new morphisms also satisfy the requisite commutativity conditions):
Embed the abstract pushout into the more complicated abstract category and validate that the universal property is still satisfied:
Compute the minimal abstract category representations of the abstract pushout and its defining universal property, respectively:
Scope (2)
Abstract pushouts can be constructed from an association of morphisms with a common domain (i.e. a generalized span), a pushout symbol, a list of names of injection morphisms, a composition symbol and an identity symbol:
A "universal object" symbol, a list of names of "universal morphisms" and a "unique morphism" symbol can also be specified, in order to characterize the universal property fully:
Abstract pushouts can also be constructed directly from an association of morphisms with a common domain (i.e. a generalized span) and a list of names of injection morphisms (plus composition and identity symbols):
Or from a morphism association (for the generalized span) with pushout, composition and identity symbols alone:
If any of these arguments is not explicitly specified, the appropriate defaults are assumed automatically:
New pushout, composition and identity symbols can be specified for any existing abstract pushout:
From an explicit association:
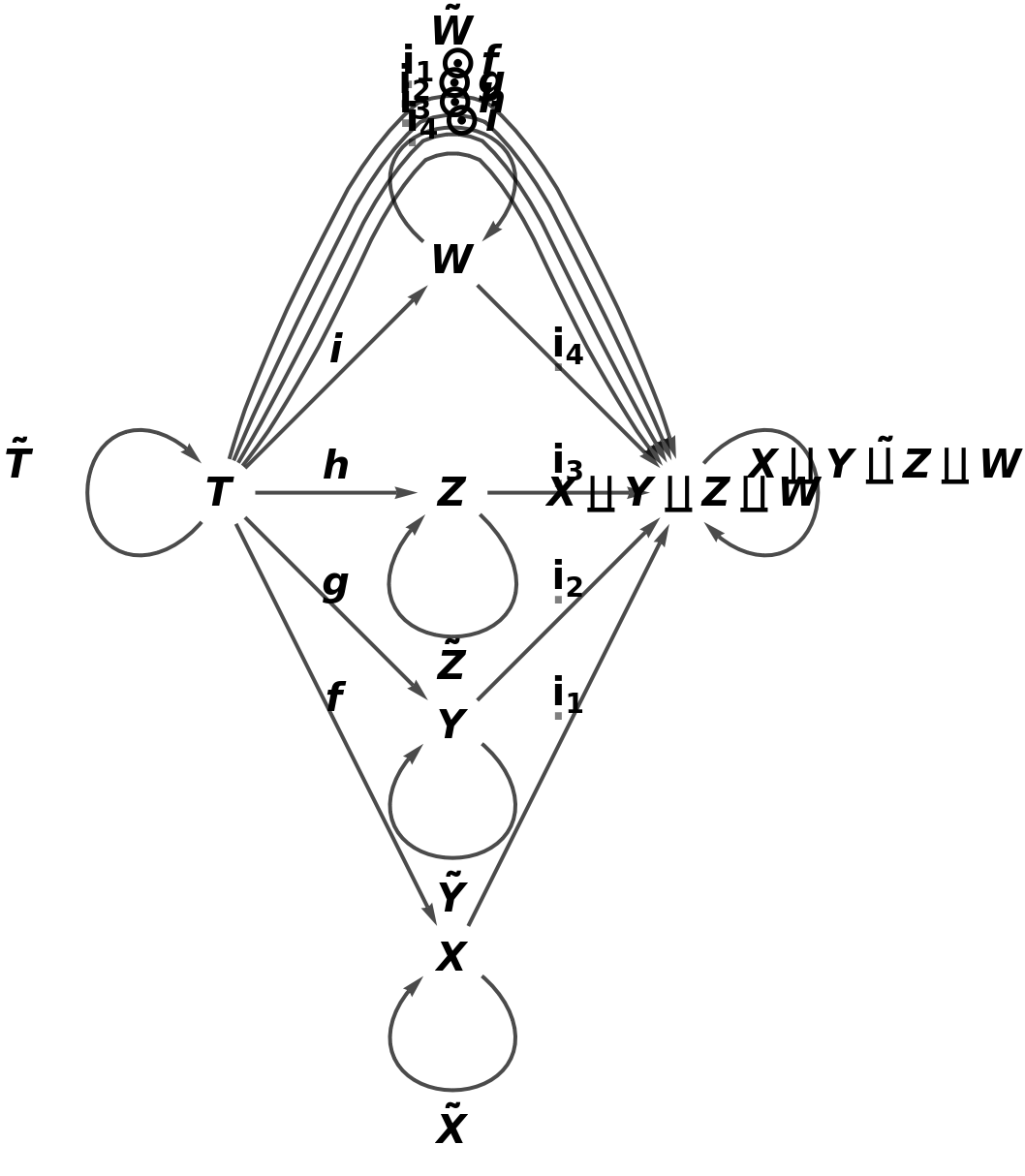
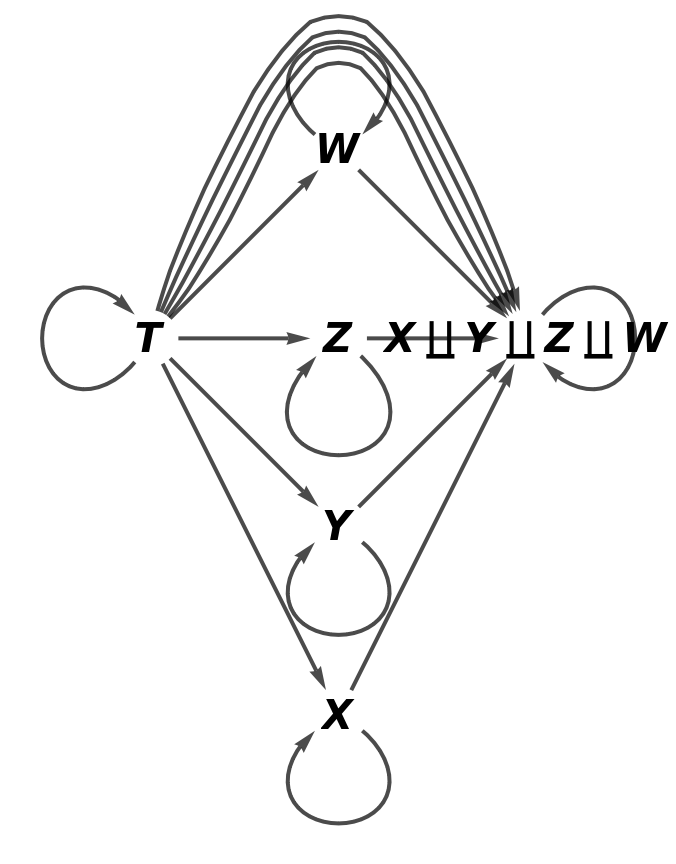
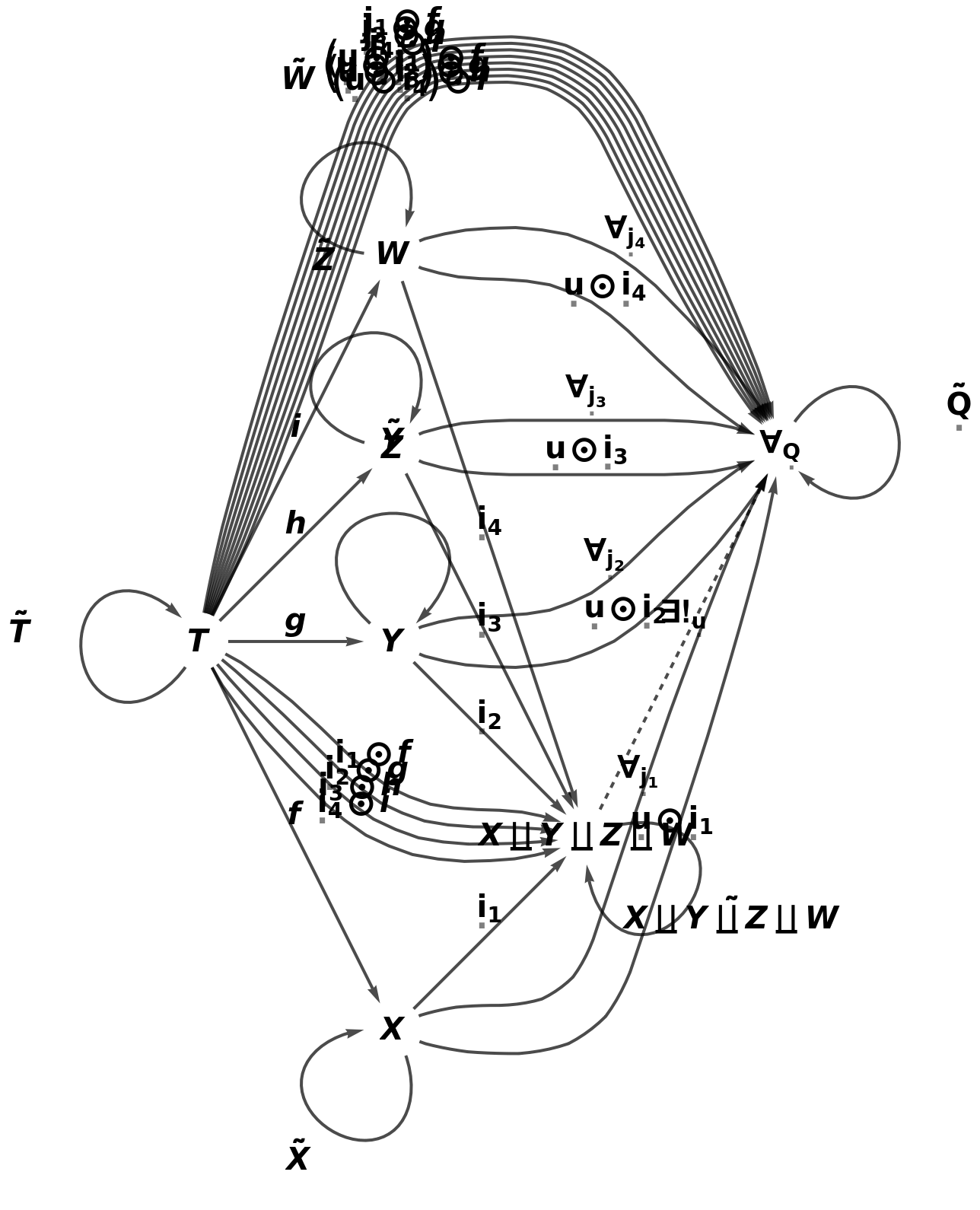
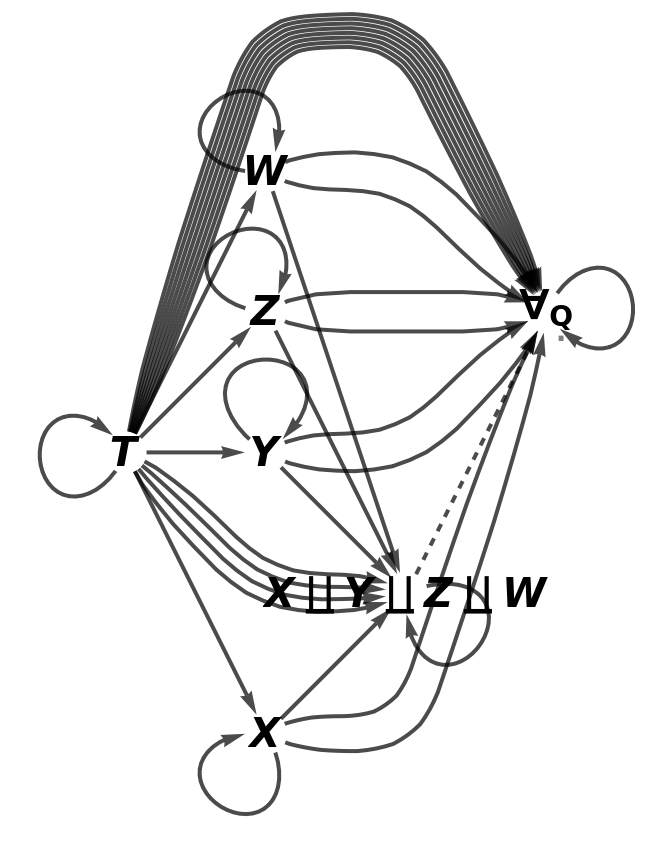
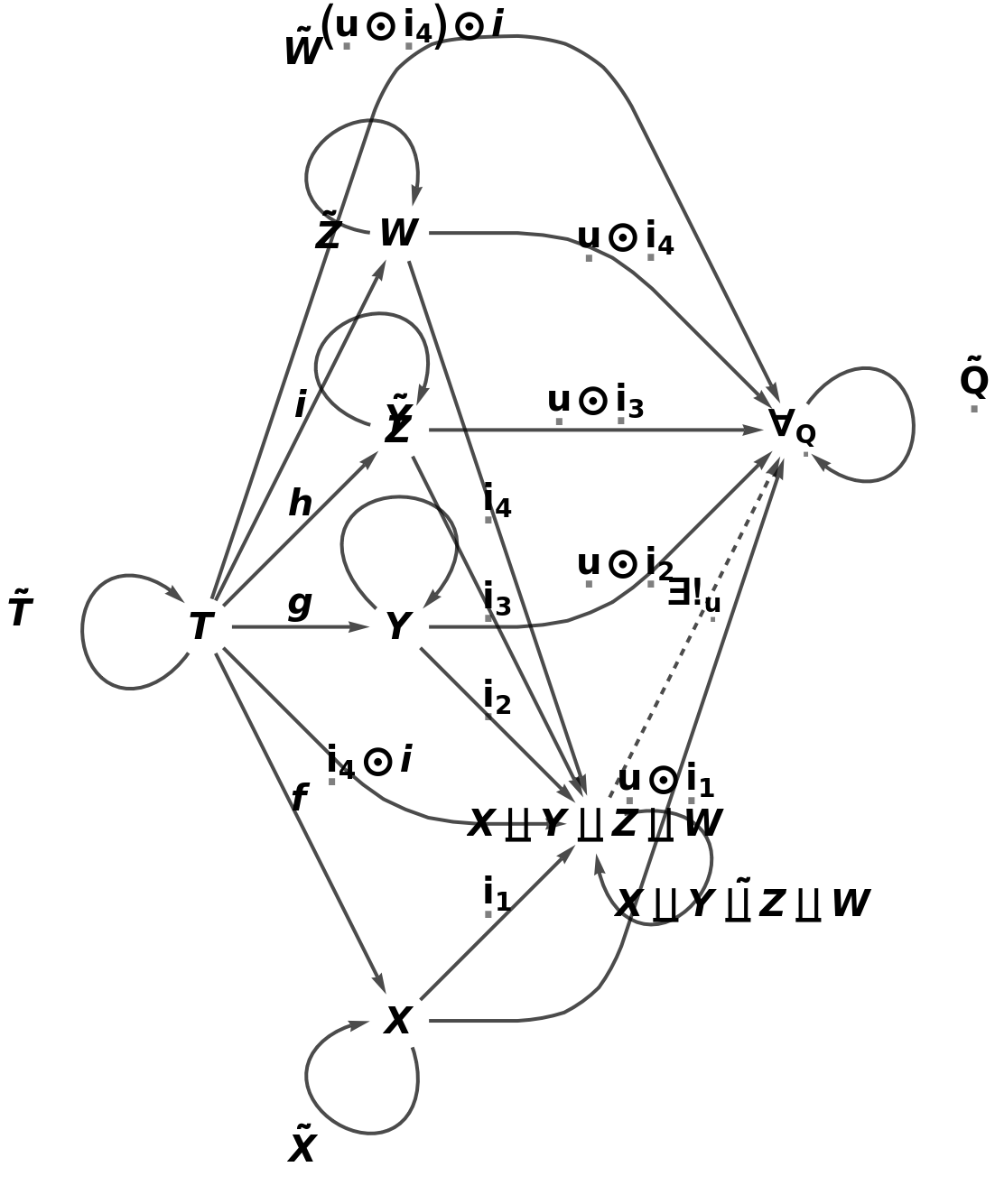
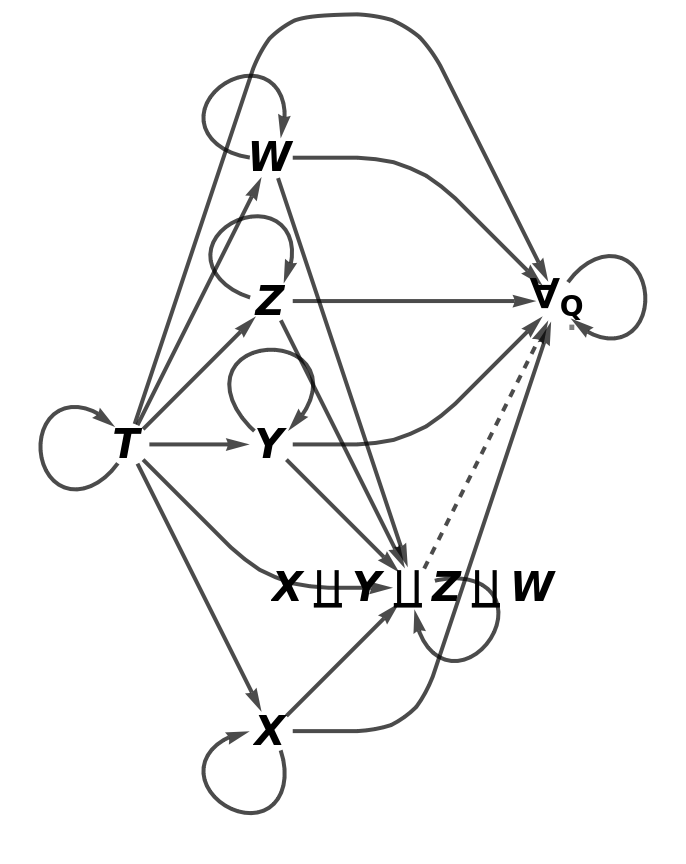
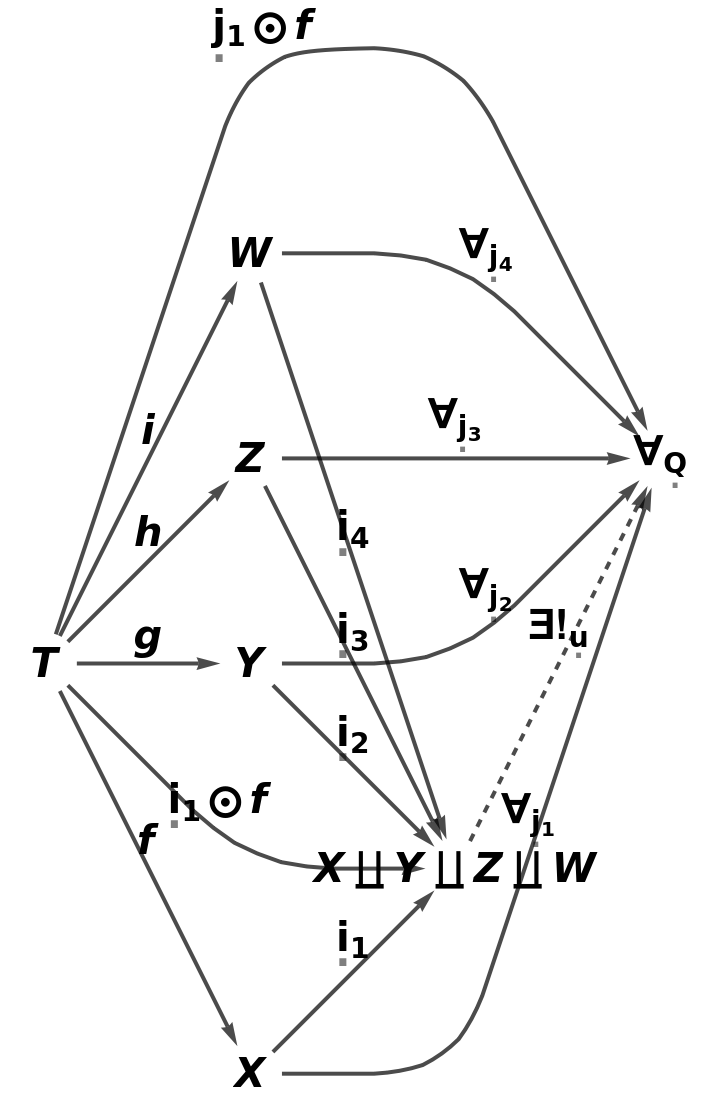
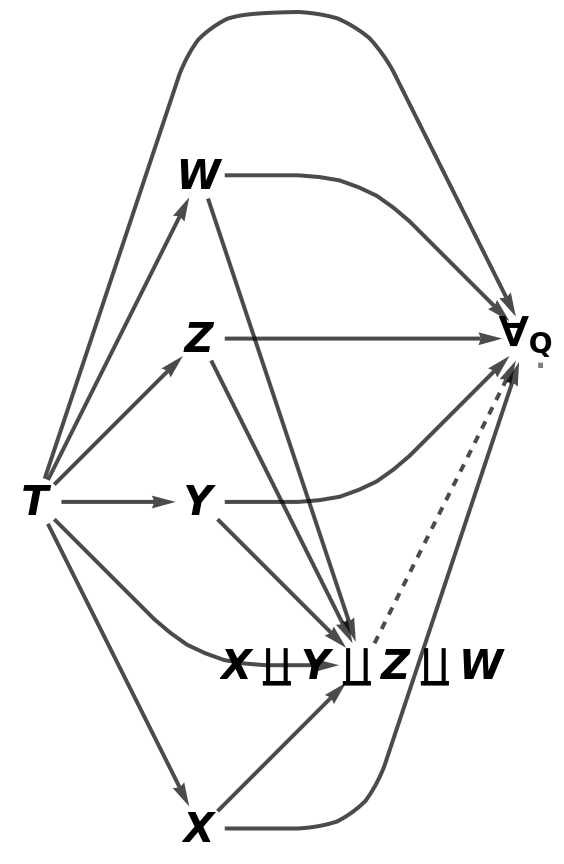
Construct an abstract pushout of morphisms f, g, h and i from a common object T to objects X, Y, Z and W:
Show the list of properties:
Show the list of objects in the abstract pushout:
Show the number of objects in the abstract pushout:
Show the association of morphisms in the abstract pushout:
Show the list of names of morphisms in the abstract pushout:
Show the list of directed edges corresponding to morphisms in the abstract pushout:
Show the number of morphisms in the abstract pushout:
Show the association of reduced morphisms, modded out by all morphism equivalences, in the abstract pushout:
Show the list of names of reduced morphisms, modded out by all morphism equivalences, in the abstract pushout:
Show the list of directed edges corresponding to reduced morphisms, modded out by all morphism equivalences, in the abstract pushout:
Show the number of reduced morphisms, modded out by all morphism equivalences, in the abstract pushout:
Show the association of simple morphisms (with all self-loops and multiedges removed) in the abstract pushout:
Show the list of names of simple morphisms (with all self-loops and multiedges removed) in the abstract pushout:
Show the list of directed edges corresponding to simple morphisms (with all self-loops and multiedges removed) in the abstract pushout:
Show the number of simple morphisms (with all self-loops and multiedges removed) in the abstract pushout:
Show the association of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) in the abstract pushout:
Show the list of names of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) in the abstract pushout:
Show the list of directed edges corresponding to reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) in the abstract pushout:
Show the number of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) in the abstract pushout:
Show the list of objects characterizing the universal property of the abstract pushout:
Show the number of objects characterizing the universal property of the abstract pushout:
Show the association of morphisms characterizing the universal property of the abstract pushout:
Show the list of names of morphisms characterizing the universal property of the abstract pushout:
Show the list of directed edges corresponding to morphisms characterizing the universal property of the abstract pushout:
Show the number of morphisms characterizing the universal property of the abstract pushout:
Show the association of reduced morphisms, modded out by all morphism equivalences, characterizing the universal property of the abstract pushout:
Show the list of names of reduced morphisms, modded out by all morphism equivalences, characterizing the universal property of the abstract pushout:
Show the list of directed edges corresponding to reduced morphisms, modded out by all morphism equivalences, characterizing the universal property of the abstract pushout:
Show the number of reduced morphisms, modded out by all morphism equivalences, characterizing the universal property of the abstract pushout:
Show the association of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract pushout:
Show the list of names of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract pushout:
Show the list of directed edges corresponding to simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract pushout:
Show the number of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract pushout:
Show the association of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract pushout:
Show the list of names of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract pushout:
Show the list of directed edges corresponding to reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract pushout:
Show the number of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract pushout:
Show the (arbitrary arity) symbol used to denote the abstract pushout operation:
Show the (binary) symbol used to denote morphism composition in the abstract pushout:
Show the (unary) symbol used to denote identity morphisms on objects in the abstract pushout:
Compute the abstract category whose morphisms represent the abstract pushout:
Compute the abstract category whose morphisms characterize the universal property of the abstract pushout:
Show the list of equations required to force the abstract pushout diagram to commute:
Show the list of equations required to force the abstract pushout diagram to commute, plus the equations implicitly imposed by the requirement that the universal property of the abstract pushout is satisfied:
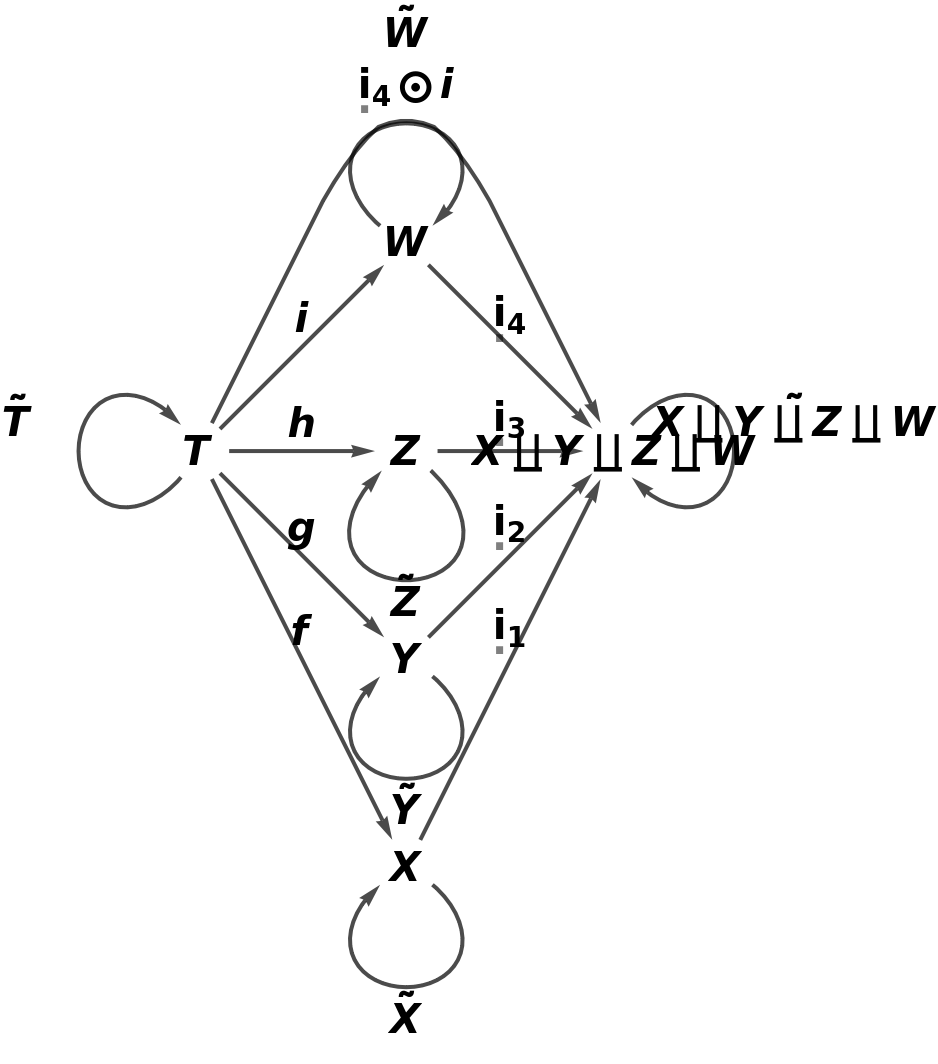
Show the full directed graph with labels on the morphisms of the abstract pushout:
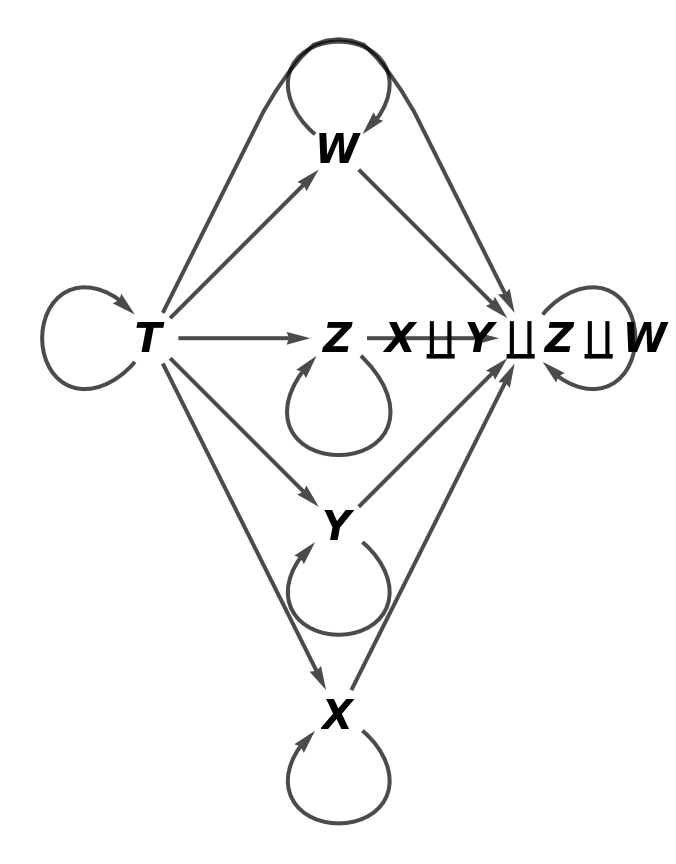
Show the full directed graph without labels on the morphisms of the abstract pushout:
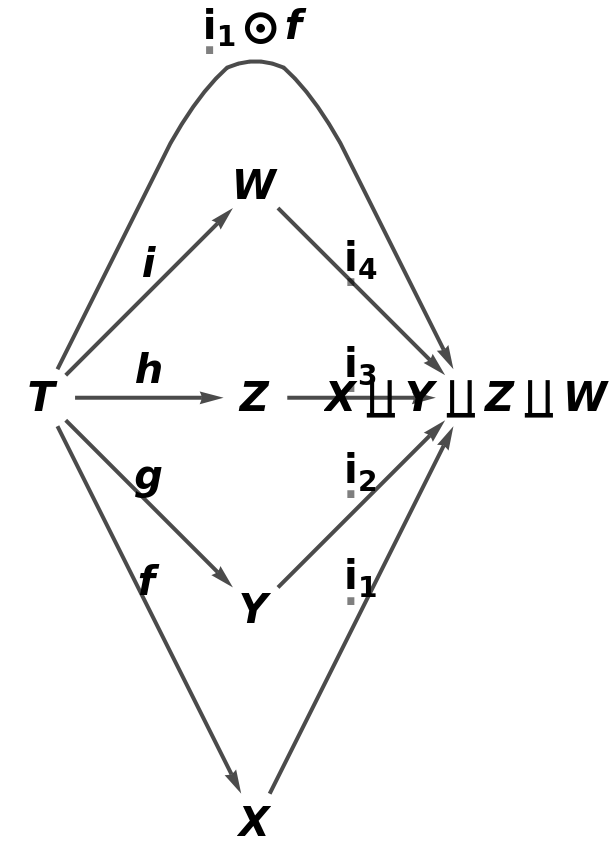
Show the reduced directed graph, with all equivalences between morphisms imposed and with labels on the morphisms of the abstract pushout:
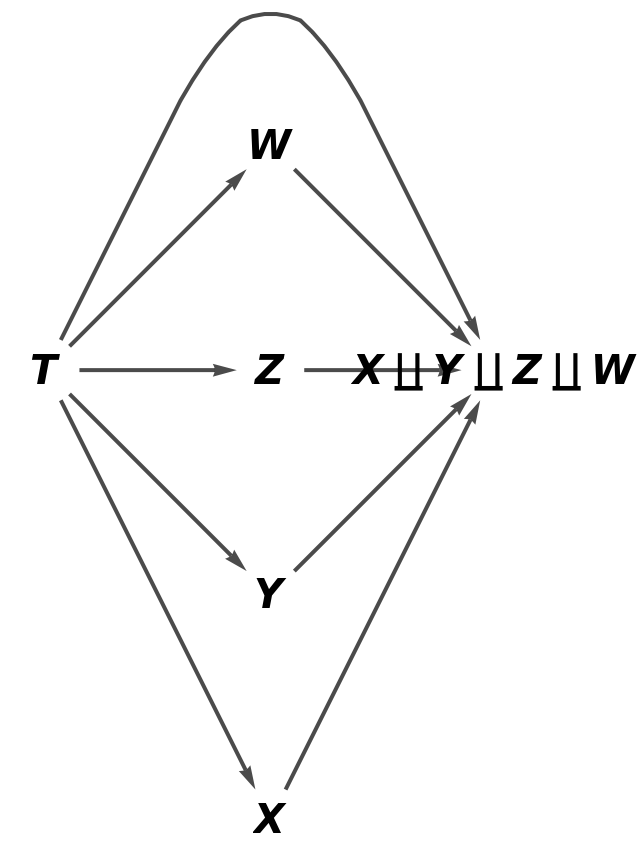
Show the reduced directed graph, with all equivalences between morphisms imposed and without labels on the morphisms of the abstract pushout:
Show the simple directed graph, with all self-loops and multiedges removed and with labels on the morphisms of the abstract pushout:
Show the simple directed graph, with all self-loops and multiedges removed and without labels on the morphisms of the abstract pushout:
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and with labels on the morphisms of the abstract pushout:
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and without labels on the morphisms of the abstract pushout:
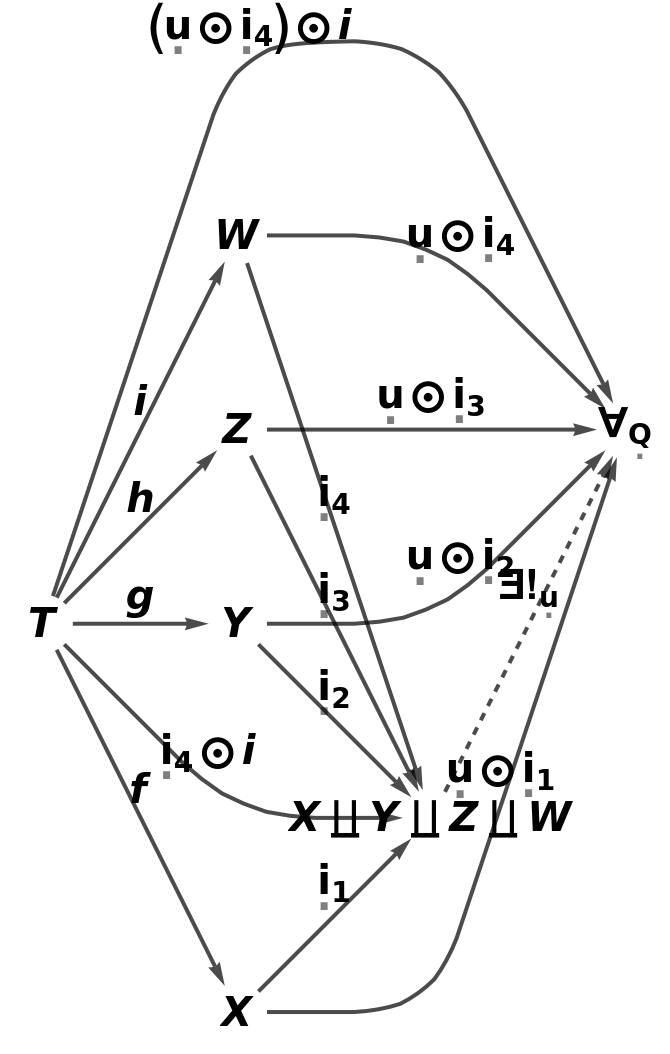
Show the full directed graph characterizing the universal property of the abstract pushout, with labels on the morphisms:
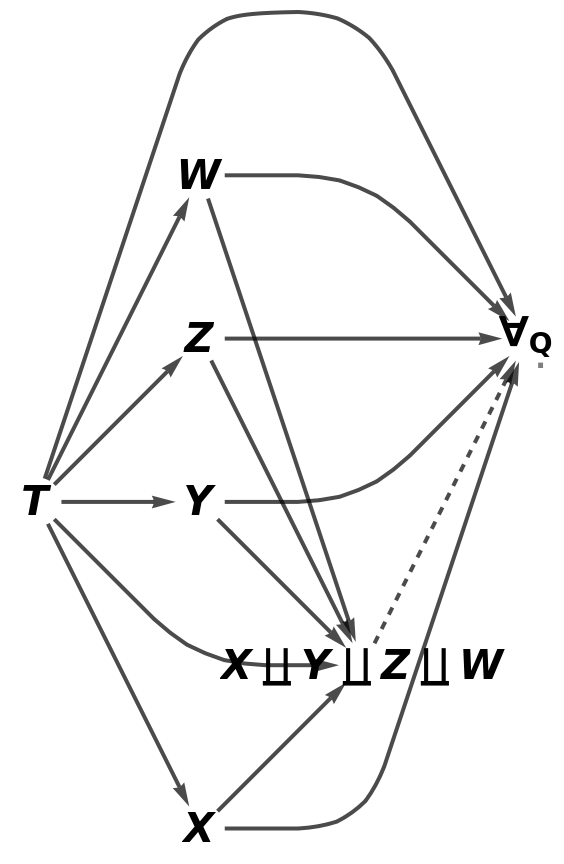
Show the full directed graph characterizing the universal property of the abstract pushout, without labels on the morphisms:
Show the reduced directed graph characterizing the universal property of the abstract pushout, with all equivalences between morphisms imposed and with labels on the morphisms:
Show the reduced directed graph characterizing the universal property of the abstract pushout, with all equivalences between morphisms imposed and without labels on the morphisms:
Show the simple directed graph characterizing the universal property of the abstract pushout, with all self-loops and multiedges removed and with labels on the morphisms:
Show the simple directed graph characterizing the universal property of the abstract pushout, with all self-loops and multiedges removed and without labels on the morphisms:
Show the reduced simple directed graph characterizing the universal property of the abstract pushout, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and with labels on the morphisms:
Show the reduced simple directed graph characterizing the universal property of the abstract pushout, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and without labels on the morphisms:
Show the explicit association form of the pushout:
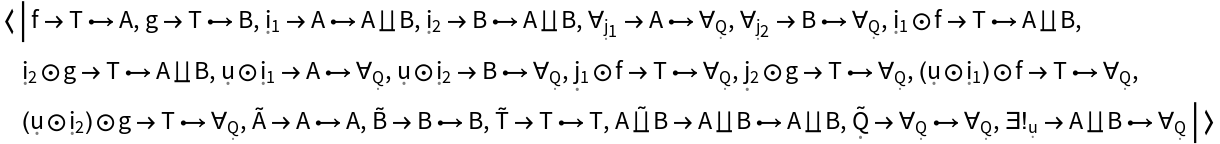
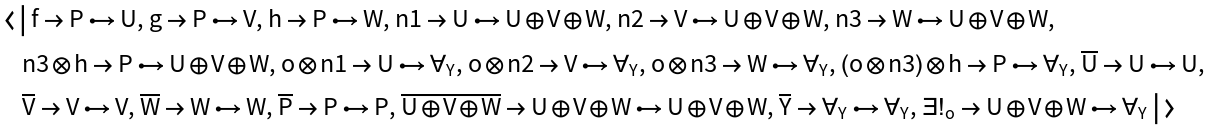
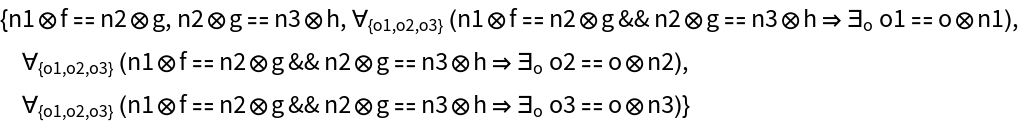

![category3 = ResourceFunction["AbstractCategory"][<|i -> {X, U}, j -> {Y, U}, k -> {X, V}, l -> {Y, V}, f -> {Z, X}, g -> {Z, Y}|>, {}, {CircleDot[i, f] == CircleDot[j, g], CircleDot[k, f] == CircleDot[l, g]}]](https://www.wolframcloud.com/obj/resourcesystem/images/35d/35d86a7f-ac4b-41a6-91e0-0bc41fdb2396/411dbec51843eca7.png)
![ResourceFunction[
"AbstractPushout"][<|"MorphismNames" -> {f, g}, "MorphismImages" -> {A, B}, "CommonDomain" -> P, "PushoutSymbol" -> CirclePlus, "InjectionMorphismNames" -> {i1, i2},
"CompositionSymbol" -> CircleTimes, "IdentitySymbol" -> OverBar, "UniversalObjectName" -> Y, "UniversalMorphismNames" -> {f1, f2}, "UniqueMorphismName" -> u|>]](https://www.wolframcloud.com/obj/resourcesystem/images/35d/35d86a7f-ac4b-41a6-91e0-0bc41fdb2396/52e2998906e264d2.png)