Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Enumerate all the neighborhoods of a hypergraph up to a given distance
ResourceFunction["HypergraphNeighborhoods"][hg,v,r] gives all the neighborhoods of the hypergraph hg up to a distance r from v. | |
ResourceFunction["HypergraphNeighborhoods"][hg,r] gives all the neighborhoods of the hypergraph hg up to a distance r from the middle vertex in a sorted vertex list. |
With the face indices of an octahedron as a hypergraph, find the first two neighborhoods of vertex 3:
| In[1]:= |
| Out[1]= | 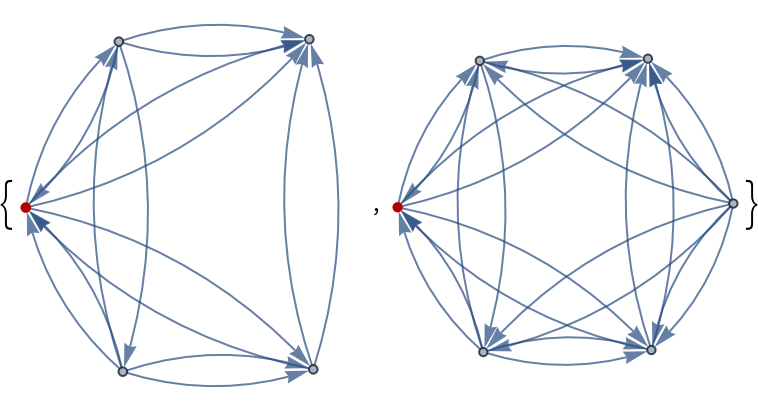 |
Since vertex 3 is the middle-low vertex in (1,2,3,4,5,6), the two-argument form of the function returns the same result:
| In[2]:= |
| Out[2]= | 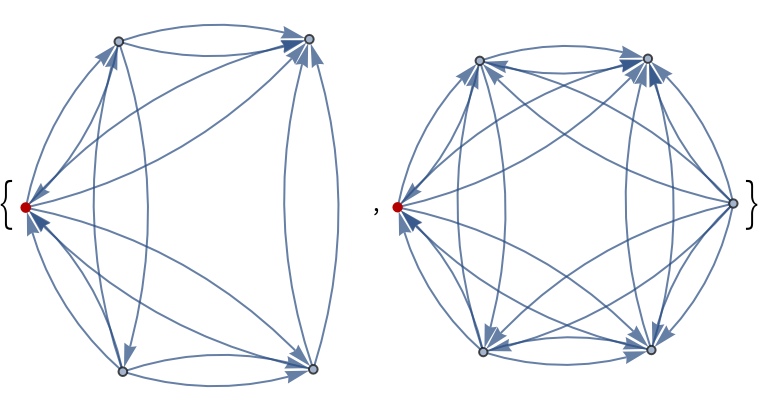 |
The edges of an octahedral graph give different neighborhoods:
| In[3]:= |
| Out[3]= | 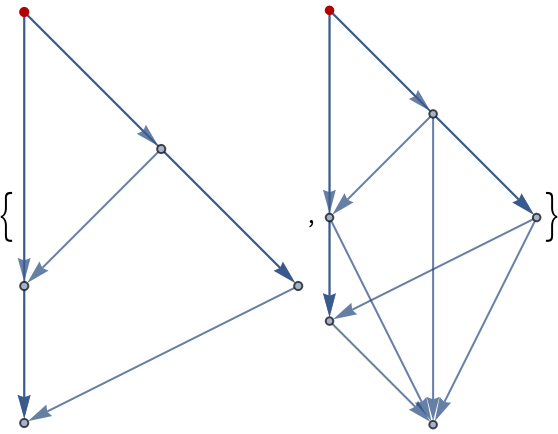 |
The first two neighborhoods of vertex 8 in a more complex hypergraph:
| In[4]:= | ![ResourceFunction[
"HypergraphNeighborhoods"][{{1, 1, 9}, {1, 9, 5}, {1, 5, 10}, {5, 10,
3}, {1, 3, 11}, {3, 11, 6}, {3, 6, 12}, {6, 12, 2}, {1, 2, 13}, {2, 13, 7}, {2, 7, 14}, {7, 14, 4}, {2, 4, 15}, {4, 15, 8}, {4, 8, 16}, {8, 16, 1}}, 8, 4]](https://www.wolframcloud.com/obj/resourcesystem/images/33d/33dfda24-4ef6-4672-983c-11fa3da1592a/69332236032aff39.png) |
| Out[4]= | 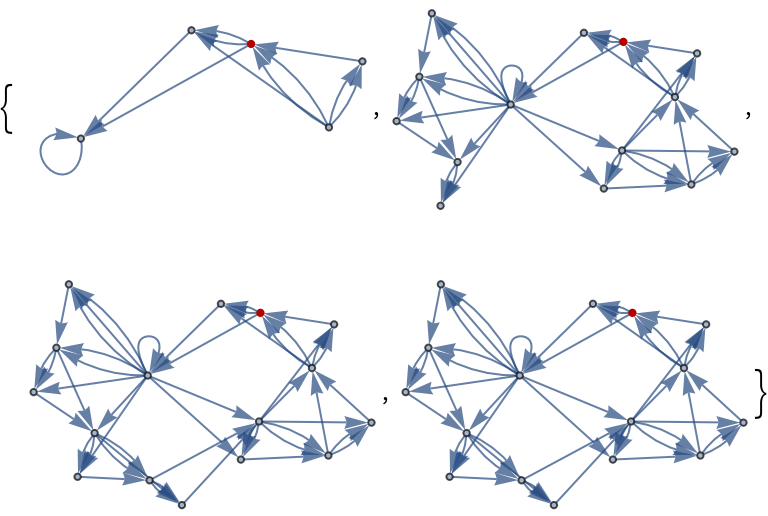 |
This work is licensed under a Creative Commons Attribution 4.0 International License