Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SubsetIndex

Source Notebook

Give the index of a subset

Contributed by: Ed Pegg Jr

ResourceFunction["SubsetIndex"][list]

gives the index of subset list.

Details and Options

Subsets are considered to be lists {a1,a2,…,ak} such that the ai are non-negative integers and strictly increasing.
Subsets are sorted by their reverse; {1,2,3} comes before {0,1,4}.
For any subset, a unique index n can be defined via .
For example: subset {2,4,6} has index .

Examples

Basic Examples (3) 

Find the index of a tuple:

In[1]:=
ResourceFunction["SubsetIndex"][{1, 2, 3}]
Out[1]=

The following 3-subset sequence can be extended to infinity:

In[2]:=
SortBy[Subsets[Range[0, 4], {3}], Reverse]
Out[2]=

The function returns indices of one to ten for these subsets:

In[3]:=
ResourceFunction["SubsetIndex"] /@ SortBy[Subsets[Range[0, 4], {3}], Reverse]
Out[3]=

Any strictly increasing list of nonnegative integers can be considered as a subset with a unique index:

In[4]:=
ResourceFunction[ "SubsetIndex"] /@ {{98, 101, 103}, {44, 102, 103}, {91, 102, 103}, {0, 9, 104}, {5, 13, 104}, {10, 16, 104}, {6, 19, 104}, {14, 21, 104}, {18, 23, 104}}
Out[4]=

The result above is a subset with a unique index:

In[5]:=
ResourceFunction["SubsetIndex"][%]
Out[5]=

Scope (3) 

Various subsets of differing lengths have index 321:

In[6]:=
index321 = {{20, 25}, {6, 8, 13}, {5, 7, 9, 10}, {3, 5, 6, 7, 10}, {3, 4, 5, 7, 8, 10}, {2, 3, 6, 7, 8, 9, 10}}; ResourceFunction["SubsetIndex"] /@ index321
Out[6]=

Some binomial representations of the number 320:

In[7]:=
Column[Row[ Riffle[Table[ TraditionalForm[ Binomial[(ToString /@ #)[[n]], ToString[n]]], {n, 1, Length[#]}], "+"]] & /@ index321, Alignment -> Center]
Out[7]=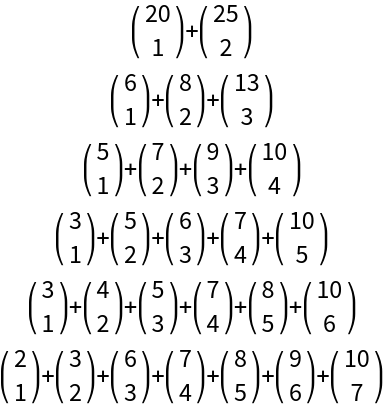

Here are some 2-subsets with their indices to show their structure:

In[8]:=
doubles = SortBy[Subsets[Range[0, 5], {2}], Reverse]; Graphics[{Text[ Style[Column[{StringJoin[ToString /@ #], ResourceFunction["SubsetIndex"][#]}, Alignment -> Center], 20], #] & /@ doubles, Blue, Line[doubles]}]
Out[8]=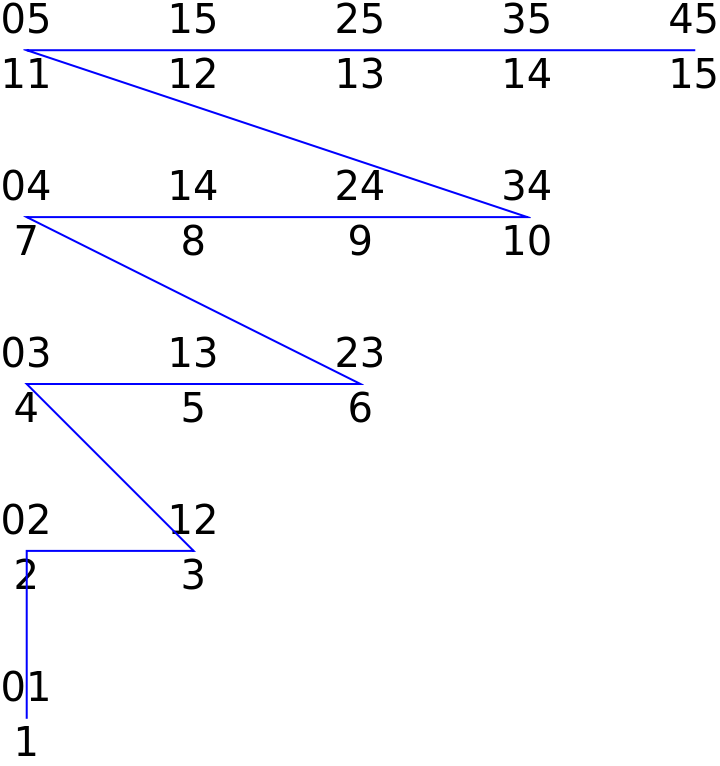

The structure of 3-subsets in 3D:

In[9]:=
triples = SortBy[Subsets[Range[0, 5], {3}], Reverse]; Graphics3D[{Text[ Style[Column[{StringJoin[ToString /@ #], ResourceFunction["SubsetIndex"][#]}, Alignment -> Center], 20], #] & /@ triples, Blue, Line[triples]}]
Out[9]=

Neat Examples (2) 

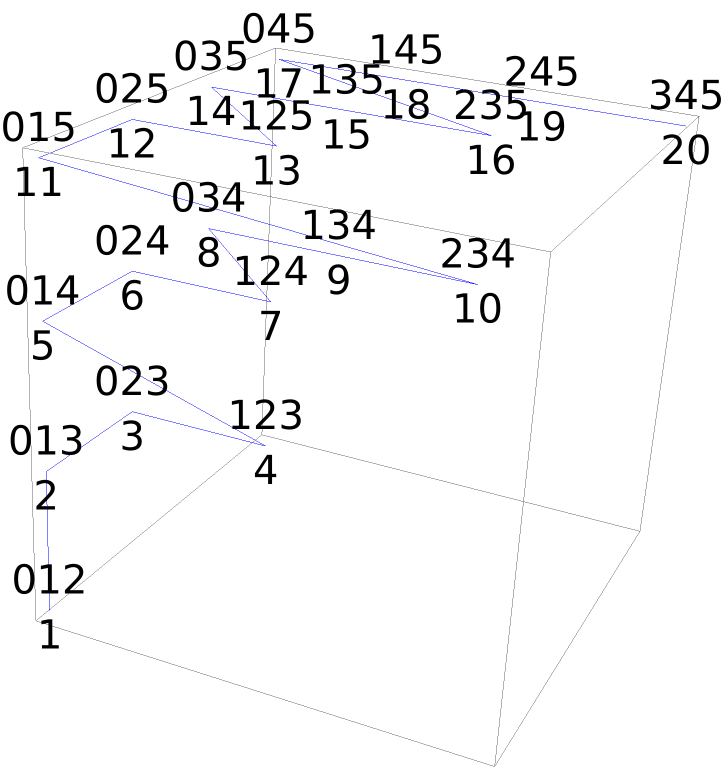Find the index of an eight-term subset:

In[10]:=
ResourceFunction["SubsetIndex"][{31, 37, 38, 47, 71, 95, 112, 122}]
Out[10]=

From that, we get the trillionth number with binary weight eight:

In[11]:=
Total[2^{31, 37, 38, 47, 71, 95, 112, 122}]
Out[11]=

Version History

  • 2.0.0 – 26 December 2019
  • 1.0.0 – 05 December 2019

Related Resources

License Information