Function Repository Resource:

Exspheres

Source Notebook

Find the exspheres of a triangle or tetrahedron

Contributed by: Minh Trinh Xuan, Ed Pegg Jr and Jan Mangaldan

ResourceFunction["Exspheres"][{p₁,p₂,p₃}]

constructs the excircles of the triangle defined by vertices p₁,p₂, and p₃.

ResourceFunction["Exspheres"][{p₁,p₂,p₃,p₄}]

constructs the exspheres of the tetrahedron defined by vertices p₁,p₂,p₃ and p₄.

Details

An excircle is also called an escribed circle. An exsphere is also called an escribed sphere.

An incircle is internally tangent to the edges of a triangle. A triangle has three excircles that are externally tangent to each side and to the other sides when extended indefinitely.

An insphere is internally tangent to the faces of a tetrahedron. A tetrahedron has four exspheres that are externally tangent to each face at its incenter and to the other faces when extended indefinitely.

ResourceFunction["Exspheres"][poly] where poly is a Triangle or Polygon is equivalent to ResourceFunction["Exspheres"][PolygonCoordinates[poly]].

ResourceFunction["Exspheres"][poly] where poly is a Tetrahedron is equivalent to ResourceFunction["Exspheres"][PolyhedronCoordinates[poly]].

The mix of 2D and 3D for Circle and Sphere follows from Insphere and Circumsphere.

Examples

Basic Examples (2)

Find the excircles for a triangle:

In[1]:=

Out[2]=

Show the excircles, incircle and infinite lines:

In[3]:=

Legended[
Graphics[{{ColorData[97, 1], InfiniteLine /@ Subsets[triangle, {2}]}, {ColorData[97, 4], circs}, {ColorData[97, 3], Insphere[triangle]}}], SwatchLegend[
ColorData[97] /@ {1, 3, 4}, {"triangle", "incircle", "excircles"}]]

Out[3]=

Scope (3)

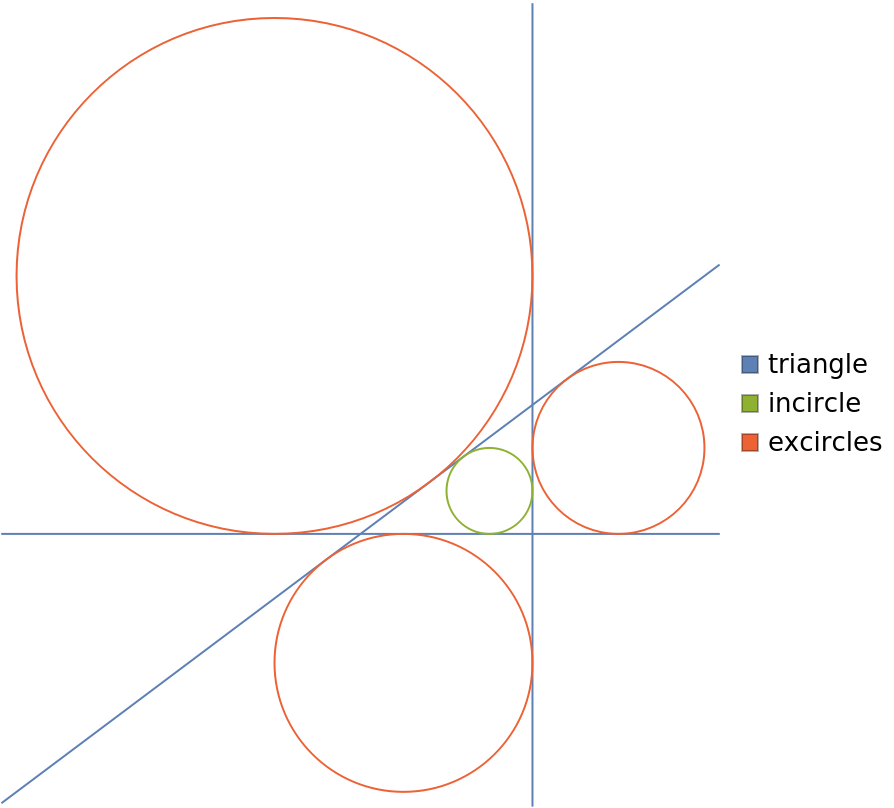A triangle:

In[4]:=

Out[4]=

Show the triangle along with its excircles:

In[5]:=

Graphics[{{FaceForm[ColorData[97, 1]], tri}, {Directive[AbsoluteThickness[5], ColorData[97, 1]], InfiniteLine /@ Partition[First[tri], 2, 1, 1]}, {Directive[
AbsoluteThickness[3], ColorData[97, 4]], ResourceFunction["Exspheres"][tri]}}]

Out[5]=

Show a tetrahedron along with its exspheres:

In[6]:=

BlockRandom[SeedRandom["tangencies", Method -> "ExtendedCA"];
tet = Tetrahedron[RandomPoint[Sphere[], 4]];
Graphics3D[{{Opacity[1/2], ColorData[97, 4], InfinitePlane /@ Subsets[PolyhedronCoordinates[tet], {3}]}, {FaceForm[], EdgeForm[AbsoluteThickness[4]], tet}, {Opacity[2/3], ColorData[97, 1], ResourceFunction["Exspheres"][tet]}}]]

Out[6]=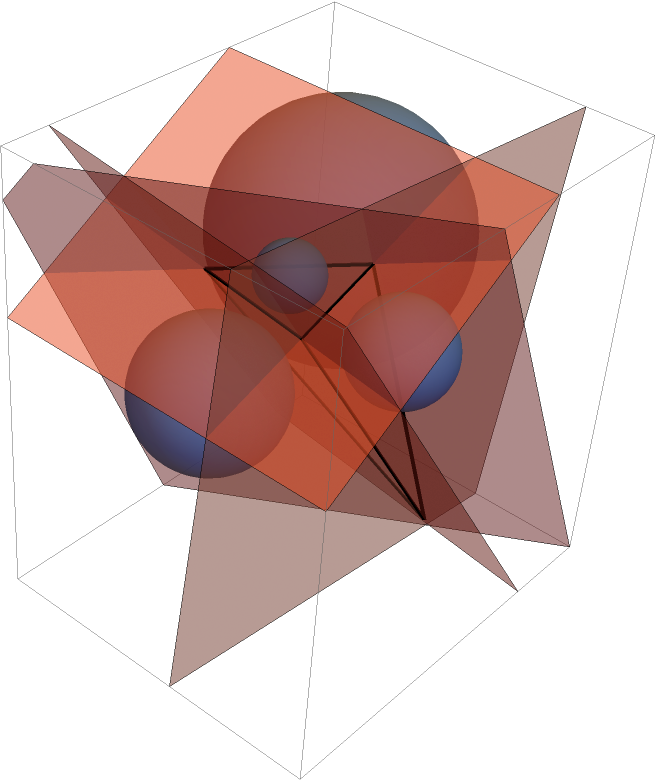

Show the insphere and exspheres of a regular tetrahedron:

In[7]:=

With[{tet = Tetrahedron[]},
Graphics3D[{{ColorData[97, 1], Insphere[tet]}, {Opacity[2/3], ColorData[97, 3], ResourceFunction["Exspheres"][tet]}}, Boxed -> False]]

Out[7]=

Neat Examples (2)

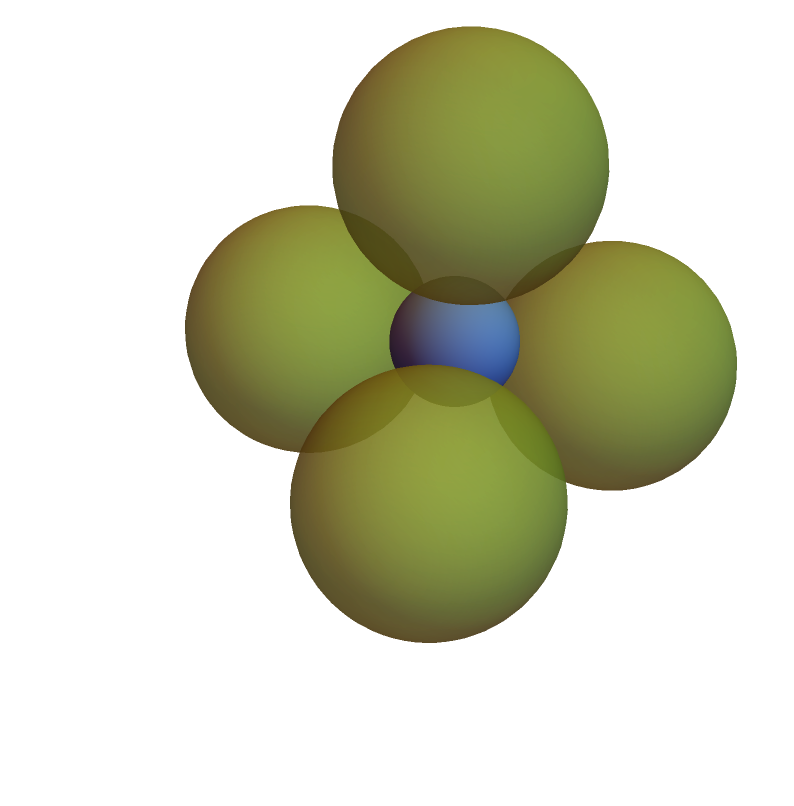Show the excircles of an arbitrary triangle:

In[8]:=

Manipulate[
Graphics[{EdgeForm[Blue], InfiniteLine /@ Subsets[{AA, BB, CC}, {2}],
Lighter[Brown], Triangle[{AA, BB, CC}], Green, ResourceFunction["Exspheres"][Triangle[{AA, BB, CC}]]}, PlotRange -> 6],
{{AA, {1, 3}}, {-4, -4}, {4, 4}, Locator}, {{BB, {-3, -1}}, {-4, -4}, {4, 4}, Locator}, {{CC, {2, -1}}, {-4, -4}, {4, 4}, Locator}, SaveDefinitions -> True]

Out[8]=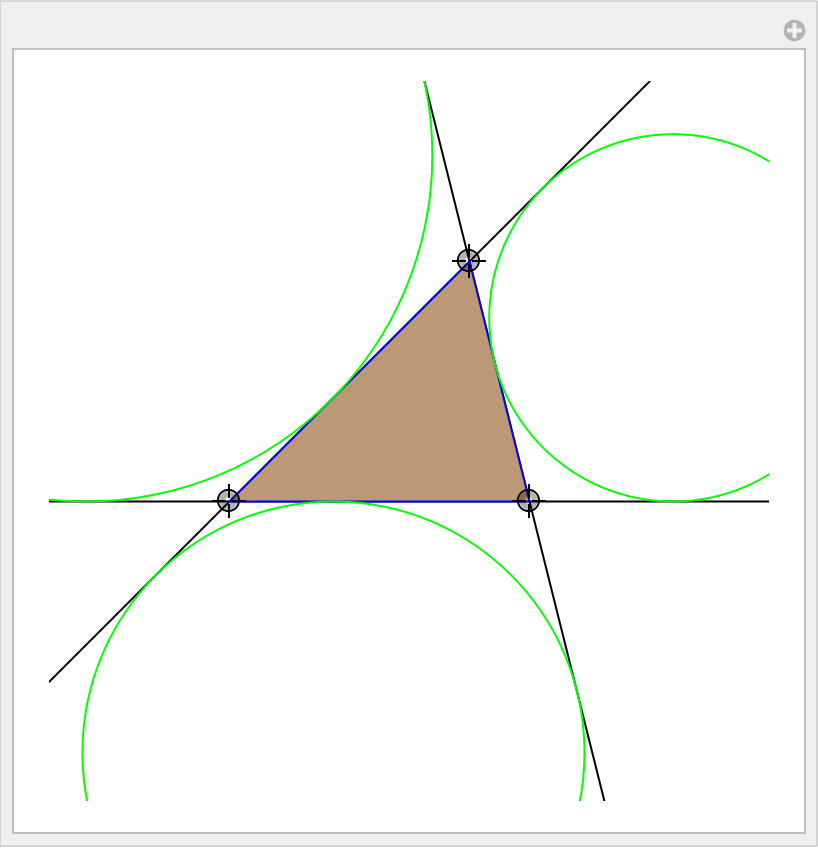

A triangle and its excircles:

In[9]:=

Out[10]=

Compute the center and the radius of the radical circle of the excircles:

In[11]:=

sl = MapApply[EuclideanDistance, Partition[tri, 2, 1, 1]];
cent = Mean[
Map[First, MapApply[RegionIntersection, Partition[
MapApply[ResourceFunction["RadicalHyperplane"], Subsets[circs, {2}]], 2, 1, 1]]]];
rad = Sqrt[
SymmetricPolynomial[2, sl] - 2 SymmetricPolynomial[3, sl]/SymmetricPolynomial[1, sl]]/2;

Show the triangle, its excircles and the radical circle altogether:

In[12]:=

Out[12]=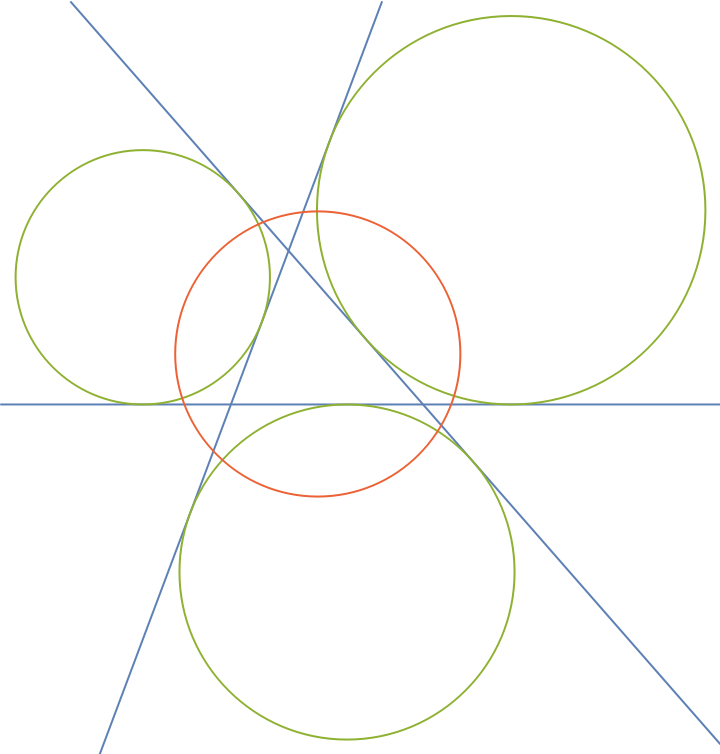

Version History

1.0.0 – 11 July 2022

Source Metadata

Citation:
- Gerber, L., "Spheres tangent to all the faces of a simplex." Journal of Combinatorial Theory, Series A, vol. 12, no. 3, 453–456, 1972. DOI: 10.1016/0097-3165(72)90106-9

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

Exspheres

Details