Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TensorIndexJuggling

Source Notebook

Given a metric, convert between covariant and contravariant components of a tensor

Contributed by: Lars Ulke-Winter

ResourceFunction["TensorIndexJuggling"][tensor,metric]

uses metric to convert tensor, having only covariant components (lower indices), into the corresponding tensor with all contravariant components (upper indices).

ResourceFunction["TensorIndexJuggling"][tensor,metric,"From"→"AllContravariant","To"→"AllCovariant"]

converts tensor, having only contravariant components, into the corresponding tensor with all covariant components.

ResourceFunction["TensorIndexJuggling"][tensor,metric,"From"→spec1,"To"→spec2]

transforms between upper and lower indices as indicated by "From" and "To".

Details and Options

Index juggling is done via the covariant tensor metric gij. To convert contravariant components to covariant, use tigij=tj.
Input tensor can be of any rank and should be a List or a StructuredArray.
The speci can be chosen from among the following: "AllCovariant", "AllContravariant" or {c1,c2,…}, where the ci are either of the literals "Con" or "Cov".

Examples

Basic Examples (4) 

Transform a covariant rank-2 tensor in a cylindrical coordinate system to its contravariant form tij→tij:

In[1]:=
ResourceFunction["TensorIndexJuggling"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"8", " ", RowBox[{"Sin", "[", RowBox[{"2", " ", "\[Phi]"}], "]"}]}], RowBox[{ FractionBox["1", "2"], " ", "r", " ", RowBox[{"Cos", "[", RowBox[{"2", " ", "\[Phi]"}], "]"}]}], RowBox[{"3", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}]}, { RowBox[{ FractionBox["1", "2"], " ", "r"}], RowBox[{ FractionBox["11", "2"], " ", SuperscriptBox["r", "2"], " "}], RowBox[{"r", " ", "8", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}]}, { RowBox[{"5", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}], RowBox[{"5", " ", "r", " ", RowBox[{"Sin", "[", "\[Phi]", "]"}]}], "2"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "0", "0"}, {"0", SuperscriptBox["r", "2"], "0"}, {"0", "0", "1"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)] // MatrixForm
Out[1]=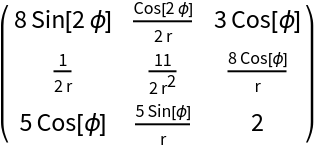

Transform a covariant rank-2 tensor in cylindrical coordinates to its mixed form tij→tij:

In[2]:=
ResourceFunction["TensorIndexJuggling"][({ {8 Sin[2 \[Phi]], 1/2 r Cos[2 \[Phi]], 3 Cos[\[Phi]]}, {1/2 r, (11/2) (r^2) , r 8 Cos[\[Phi]]}, {5 Cos[\[Phi]], 5 r Sin[\[Phi]], 2} }), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "0", "0"}, {"0", SuperscriptBox["r", "2"], "0"}, {"0", "0", "1"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), "From" -> "AllCovariant", "To" -> {"Cov", "Con"}] // MatrixForm
Out[3]=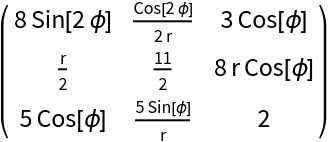

Convert tij→tij for a SymmetrizedArray:

In[4]:=
ResourceFunction["TensorIndexJuggling"][ SymmetrizedArray[{{1, 1} -> Subscript[\[Sigma], 11], {1, 2} -> Subscript[\[Sigma], 12], {2, 2} -> Subscript[\[Sigma], 22]}, {2, 2}, Symmetric[{1, 2}]], \!\(\* TagBox[ RowBox[{"\[IndentingNewLine]", RowBox[{"CoordinateChartData", "[", RowBox[{"\"\<Polar\>\"", ",", " ", "\"\<Metric\>\"", ",", RowBox[{"{", RowBox[{"r", ",", "\[Phi]"}], "}"}]}], "]"}]}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\) ]
Out[4]=

Attempting the conversion tij→tij changes nothing:

In[5]:=
ResourceFunction["TensorIndexJuggling"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"8", " ", RowBox[{"Sin", "[", RowBox[{"2", " ", "\[Phi]"}], "]"}]}], RowBox[{ FractionBox["1", "2"], " ", "r", " ", RowBox[{"Cos", "[", RowBox[{"2", " ", "\[Phi]"}], "]"}]}], RowBox[{"3", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}]}, { RowBox[{ FractionBox["1", "2"], " ", "r"}], RowBox[{ FractionBox["11", "2"], " ", SuperscriptBox["r", "2"], " "}], RowBox[{"r", " ", "8", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}]}, { RowBox[{"5", " ", RowBox[{"Cos", "[", "\[Phi]", "]"}]}], RowBox[{"5", " ", "r", " ", RowBox[{"Sin", "[", "\[Phi]", "]"}]}], "2"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "0", "0"}, {"0", SuperscriptBox["r", "2"], "0"}, {"0", "0", "1"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), "To" -> "AllCovariant"] // MatrixForm
Out[8]=

Scope (17) 

Index juggling of base vectors in cylindrical frame (3) 

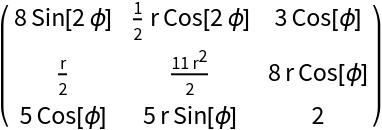Start with a covariant base:

In[9]:=
gCov = {{Cos[\[Phi]], Sin[\[Phi]], 0}, {-r Sin[\[Phi]], r Cos[\[Phi]], 0}, {0, 0, 1}};

Get the contravariant base through raising the index:

In[10]:=
gCon = (ResourceFunction["TensorIndexJuggling"][{g1, g2, g3}, CoordinateChartData["Cylindrical", "Metric", {r, \[Phi], z}]]) /. {g1 -> gCov[[1]], g2 -> gCov[[2]], g3 -> gCov[[3]]} // Simplify
Out[10]=

Check the orthonormality relationship gi·gj=δij:

In[11]:=
Simplify@( { {gCov[[1]] . gCon[[1]], gCov[[1]] . gCon[[2]], gCov[[1]] . gCon[[3]]}, {gCov[[2]] . gCon[[1]], gCov[[2]] . gCon[[2]], gCov[[2]] . gCon[[3]]}, {gCov[[3]] . gCon[[1]], gCov[[3]] . gCon[[2]], gCov[[3]] . gCon[[3]]} } ) // MatrixForm
Out[11]=

Index juggling of the metric tensor in cylindrical frame (4) 

Start with the metric for cylindrical coordinates in Euclidean space:

In[12]:=
metricCyl = CoordinateChartData["Cylindrical", "Metric", {r, \[Phi], z}]; metricCyl // MatrixForm
Out[10]=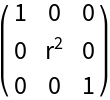

Get the contravariant components of the metric:

In[13]:=
(ResourceFunction["TensorIndexJuggling"][metricCyl, metricCyl, From -> "AllCovariant", To -> "AllContravariant"]) // Simplify // MatrixForm
Out[11]=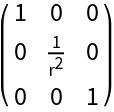

This result is the same as the Wolfram Language built-in function:

In[14]:=
CoordinateChartData["Cylindrical", "InverseMetric", {r, \[Phi], z}] // MatrixForm
Out[15]=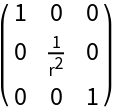

In[16]:=
(ResourceFunction["TensorIndexJuggling"][metricCyl, metricCyl, From -> "AllCovariant", "To" -> {"Con", "Cov"}]) // Simplify // MatrixForm
Out[17]=

Contraction of two opposing indices leads to an invariant scalar (6) 

Start with the metric for cylindrical coordinates in Euclidean space:

In[18]:=
metricCyl = CoordinateChartData["Cylindrical", "Metric", {r, \[Phi], z}]; metricCyl // MatrixForm
Out[73]=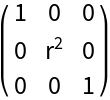

Define a Cartesian rank-2 tensor:

In[74]:=
SeedRandom[314]; t = RandomInteger[10, {3, 3}]; t // MatrixForm
Out[75]=

Contract the indices:

In[76]:=
tContractedInv = TensorContract[t, {1, 2}]
Out[76]=

Use the resource function TensorCoordinateTransform to transform t to cylindrical coordinates with covariant transformation behavior tij:

In[77]:=
tInCylCovCov = ResourceFunction["TensorCoordinateTransform"][ t, (CoordinateTransformData["Cylindrical" -> "Cartesian", "MappingJacobian", {r, \[Phi], z}])\[Transpose], "TransformationBehavior" -> "AllCovariant"] // Simplify[#, r > 0] &; tInCylCovCov // MatrixForm
Out[129]=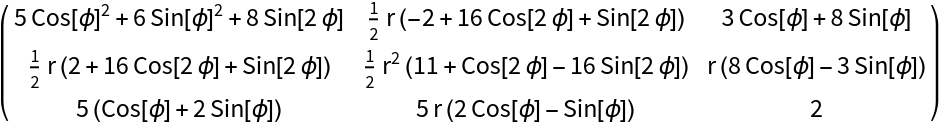

Contraction should not be invariant:

In[130]:=
TensorContract[tInCylCovCov, {1, 2}] // Simplify
Out[130]=

But contraction of opposing indices should be:

In[131]:=
TensorContract[ ResourceFunction["TensorIndexJuggling"][tInCylCovCov, metricCyl, "To" -> {"Cov", "Con"}], {1, 2}] // Simplify
Out[131]=

Contraction of opposing indices in a rank-6 tensor  (4) 

Start with a rank-6 tensor in a Cartesian basis and form the contraction tijkijkl:

In[132]:=
SeedRandom[3141] t = RandomInteger[{-10, 10}, {3, 3, 3, 3, 3, 3}]; TensorContract[t, {{1, 4}, {2, 5}, {3, 6}}]
Out[132]=

Transform to an different affine system with given mapping:

In[133]:=
tAllCov = ResourceFunction["TensorCoordinateTransform"][t, mapping = ( { {2, 3, 1}, {1, 2, 2}, {1, 0, 1} } ), "TransformationBehavior" -> "AllContravariant"];

Contraction of the indices of the same type does not lead to an invariant:

In[134]:=
TensorContract[tAllCov, {{1, 4}, {2, 5}, {3, 6}}]
Out[134]=

Contraction of the right opposing index pairs, after index juggling, leads to the same result as in the original coordinate system:

In[135]:=
TensorContract[ tConConConCovCovCov = ResourceFunction["TensorIndexJuggling"][tAllCov, metric = ( { {mapping[[1]] . mapping[[1]], mapping[[1]] . mapping[[2]], mapping[[1]] . mapping[[3]]}, {mapping[[2]] . mapping[[1]], mapping[[2]] . mapping[[2]], mapping[[2]] . mapping[[3]]}, {mapping[[3]] . mapping[[1]], mapping[[3]] . mapping[[2]], mapping[[3]] . mapping[[3]]} } ), "From" -> "AllContravariant", "To" -> {"Con", "Con", "Con", "Cov", "Cov", "Cov"}], {{1, 4}, {2, 5}, {3, 6}}]
Out[135]=

Properties & Relations (1) 

If the mapping rule between the two coordinate frames exists, index juggling can also be done using the resource function TensorCoordinateTransform. However, if only the metric of the space is available, then TensorIndexJuggling is recommended:

In[136]:=
(ResourceFunction["TensorCoordinateTransform"][ t = RandomInteger[{-10, 10}, {3, 3, 3, 3, 3, 3}], mapping = ( { {2, 3, 1}, {1, 2, 2}, {1, 0, 1} } ), "TransformationBehavior" -> {"Cov", "Con", "Cov", "Con", "Cov", "Con"}]) == (ResourceFunction["TensorIndexJuggling"][ ResourceFunction["TensorCoordinateTransform"][t, mapping, "TransformationBehavior" -> "AllCovariant"], ( { {mapping[[1]] . mapping[[1]], mapping[[1]] . mapping[[2]], mapping[[1]] . mapping[[3]]}, {mapping[[2]] . mapping[[1]], mapping[[2]] . mapping[[2]], mapping[[2]] . mapping[[3]]}, {mapping[[3]] . mapping[[1]], mapping[[3]] . mapping[[2]], mapping[[3]] . mapping[[3]]} } ), "To" -> {"Cov", "Con", "Cov", "Con", "Cov", "Con"}])
Out[136]=

Publisher

Lars Ulke-Winter

Version History

  • 1.0.0 – 03 October 2019

Source Metadata

  • Citation:
    • Grinfeld, P., Introduction to Tensor Analysis and the Calculus of Moving Surfaces. New York: Springer Science+Business Media, 2013.

Related Resources

License Information