Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the three Lucas circles of a given triangle
ResourceFunction["LucasCircles"][{p1,p2,p3}] gives the three Lucas circles for a triangle with vertices p1,p2 and p3. | |
ResourceFunction["LucasCircles"][{p1,p2,p3},property] returns extra related geometric objects of the Lucas circles for the given property. | |
ResourceFunction["LucasCircles"][{p1,p2,p3},{prop1,…}] returns a list of properties. |
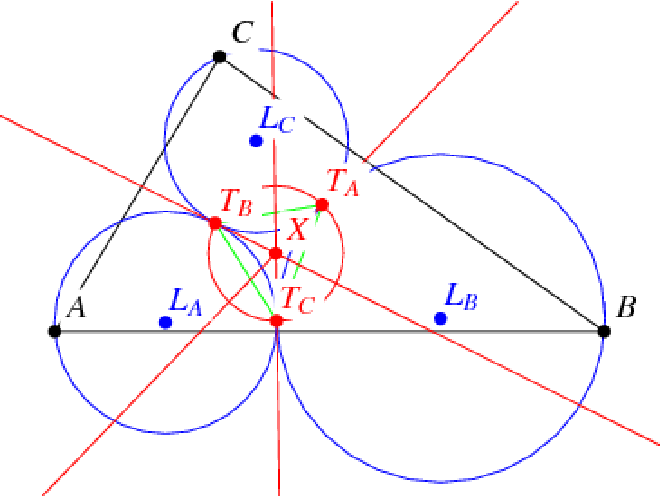
| "Circles" | the three Lucas circles of a triangle |
| "LucasCircles" | same as "Circles" |
| "InscribedSubtriangles" | the three triangles inscribed in the three Lucas circles |
| "InscribedSquares" | the three inscribed squares that share one side with the triangle, used in constructing the Lucas circles |
| "LucasContactPoints" | the three contact points between pairs of Lucas circles |
| "LucasOuterSoddyCircle" | the circle that is internally tangent to the three Lucas circles |
| "LucasInnerSoddyCircle" | the circle that is externally tangent to the three Lucas circles |
| "LucasSideSoddyCircles" | the three circles that are each externally tangent to two Lucas circles and internally tangent to the circumcircle |
| All | an association including all properties given above |
Give the three Lucas circles of a triangle:
| In[1]:= |
| Out[1]= |
An equivalent specification:
| In[2]:= |
| Out[2]= |
Find a list of properties for a triangle:
| In[3]:= |
| Out[3]= |  |
Visualize the three Lucas circles along with the reference triangle:
| In[4]:= | ![tri = Triangle[{{0, 0}, {1.2, 4}, {5, 0.5}}];
Graphics[{
{Opacity[0.2], Orange, tri},
{Opacity[0.4], ResourceFunction["LucasCircles"][tri]}
}] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/46843d8fe49bbc16.png) |
| Out[4]= | 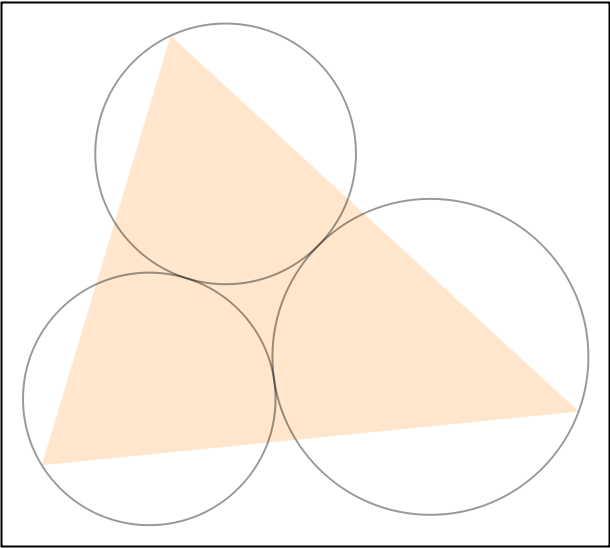 |
Find the Lucas circles for several triangles:
| In[5]:= | ![triList = Triangle[{
{{0, 0}, {1.2, 4}, {5, 0.5}},
{{0.5, -0.5}, {1.2, 3}, {5, 0}}
}];](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/2f2fbb0a3e683b58.png) |
| In[6]:= |
| Out[6]= |
Display all available information from LucasCircles in a Dataset:
| In[7]:= |
| Out[7]= |  |
The Lucas circles are constructed in the following way via hatch-filled three-way inscribed squares:
| In[8]:= |
| In[9]:= | ![GraphicsRow[MapThread[
Graphics[{
{Transparent, EdgeForm[{Blue, Thick}], Triangle@tri},
{Opacity[0.1], #1},
{Opacity[0.8], #3, Dashed, ResourceFunction["LucasCircles"][tri, "LucasOuterSoddyCircle"]},
{Opacity[0.4], HatchFilling[\[Pi]/4.8, 3], EdgeForm[{Thick, Opacity[0.6]}], #2},
}] &,
ResourceFunction["LucasCircles"][
tri, #] & /@ {"InscribedSubtriangles", "InscribedSquares", "LucasCircles"}
]] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/4de6f76c2c4e8df1.png) |
| Out[9]= | 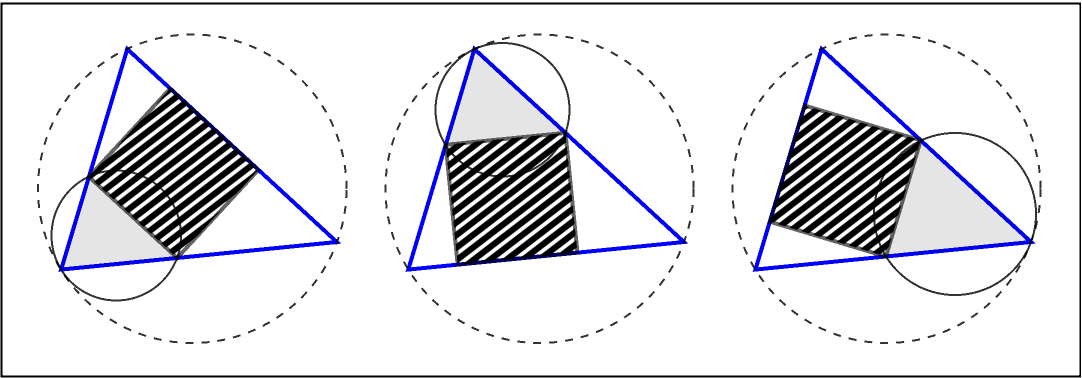 |
The three Lucas circles are externally tangent to each other. They are internally tangent to the circumcircle of the reference triangle:
| In[10]:= |
| In[11]:= | ![Graphics[{
{Transparent, EdgeForm[{Blue, Thick}], Triangle@tri},
{Opacity[0.3], Thick, lc["Circles"], lc["InscribedSubtriangles"], lc["LucasOuterSoddyCircle"]},
{Blue, Thick, PointSize[0.03], lc["LucasContactPoints"], lc["LucasInnerSoddyCircle"], Point /@ tri}
}]](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/6675c24498957586.png) |
| Out[11]= | 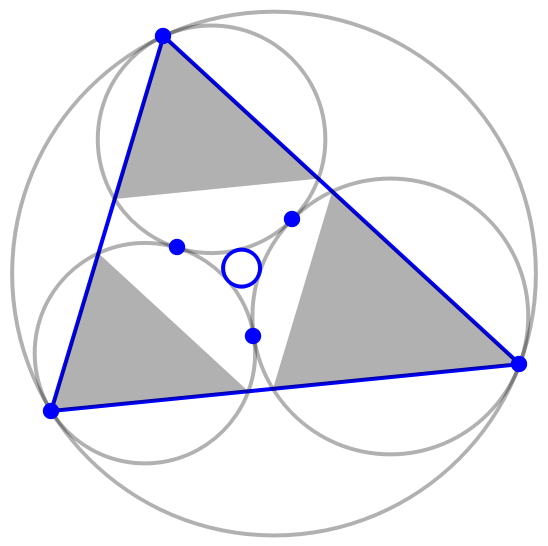 |
The smallest blue circle, the Lucas inner circle, is the inverse of the circumcircle with respect to the radical circle of the three Lucas circles (a circle through the pairwise contact points):
| In[12]:= |
| In[13]:= | ![LIC = ResourceFunction["CircleInversion"][
CircleThrough[
ResourceFunction["LucasCircles"][tri, "LucasContactPoints"] /. Point -> Identity],
TriangleConstruct[tri, "Circumcircle"]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/5f61210ffbc7edcc.png) |
| Out[13]= |
| In[14]:= |
| Out[14]= |
The radius of the Lucas inner circle can also be computed using the Brocard angle:
| In[15]:= | ![With[{cotBA = Total@Cot[PlanarAngle /@ NestList[RotateLeft, tri, 2]]},
TriangleMeasurement[tri, "Circumradius"]/(4*cotBA + 7)]](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/62a3be52d44e6297.png) |
| Out[15]= |
| In[16]:= |
| Out[16]= |
There are three circles that are each tangent to two Lucas circles externally and the circumcircle internally that are denoted by solid disks in the following diagram (in total there are 6+9=15 contact points). In fact, they are the inverses of the Lucas circles with respect to some large circles (of the same color) through two vertices of the reference triangle and one contact point of a pair of Lucas circles. Moreover, the arcs intersect orthogonally with two Lucas circles and the circumcircle of the reference triangle, respectively:
| In[17]:= |
| In[18]:= | ![config = {{
Hue[0.1],
Hue[0.3],
Hue[0.7]},
lc["Circles"],
MapThread[CircleThrough[
Append[#, #2]]& , {
Partition[
RotateLeft[tri], 2, 1, 1],
ReplaceAll[
lc["LucasContactPoints"], Point -> Identity]}],
ReplaceAll[
lc["LucasSideSoddyCircles"], Circle -> Disk]};
Graphics[{
{Dashed, lc["LucasOuterSoddyCircle"]},
{Transparent, EdgeForm[Dashed], Triangle@tri},
MapThread[{#1, {Thickness[0.01], #2, #3}, #4} &, config],
MapThread[{#1, PointSize[0.03], #2} &, {{Hue[0.1], Hue[0.3], Hue[
0.7]}, lc["LucasContactPoints"]}]
}, Sequence[
PlotRange -> {{-0.5, 5.5}, {-1.5, 4.5}}, ImageSize -> 360]] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/660f0009b5640588.png) |
| Out[18]= |  |
Create a Sierpiński sieve–like fractal with the Lucas circles of the reference triangle and its subtriangles recursively. The top vertex of the largest triangle is a Locator controller. Drag it around to change the Lucas circle fractal:
| In[19]:= | ![DynamicModule[{circles, colorList},
Manipulate[
circles = (TriangleConstruct[#, "Circumcircle"] & /@ Flatten[NestList[
LucasCirclesFractal, {Triangle[{{0, 0}, p, {5, 0.5}}]}, 4]]) /. Circle -> Disk;
colorList = RotateRight[Hue /@ Sqrt[(Rescale@Range[Length[circles]])], n];
Graphics[{Opacity[0.6], Transpose[{colorList, circles}]},
PlotRange -> {{-0.5, 5.5}, {-1.5, 4.5}}, ImageSize -> 360],
{{p, {1.2, 4}}, Locator, Appearance -> Graphics[{Red,
Table[
Circle[{0, 0}, i], {i, 3}]}, ImageSize -> 20]},
{{n, 1, "Color arrangement"}, 1, 80, 3},
SynchronousUpdating -> False, Initialization :> (LucasCirclesFractal[triList_] := Flatten[(ResourceFunction["LucasCircles"][#, "InscribedSubtriangles"]) & /@ triList])]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ac/2acddb06-47eb-4223-8d6d-498d3147ca10/64529bf342b85cf4.png) |
| Out[19]= | 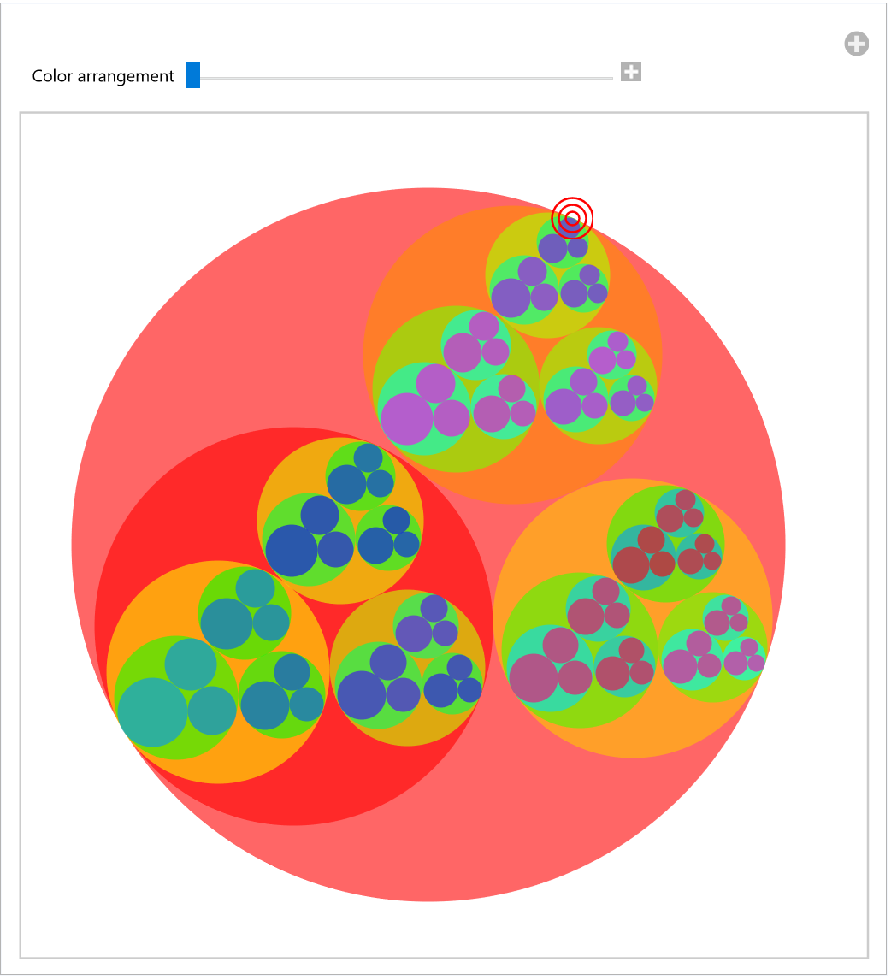 |
This work is licensed under a Creative Commons Attribution 4.0 International License