Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the intersection of two lines
ResourceFunction["LineIntersection"][{a,b},{c,d}] returns the intersection of the infinite lines through points a to b and points c to d. | |
ResourceFunction["LineIntersection"][{{a,b},{c,d}}] returns the intersection of the infinite lines through points a to b and points c to d. |
Fine a line intersection:
| In[1]:= | ![line1 = {{0, 0}, {1, 1}};
line2 = {{0, 1}, {1, 0}};
p = ResourceFunction[
"LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/1ccde5a65b9322eb.png) |
| Out[3]= |
Show it:
| In[4]:= |
| Out[4]= |  |
Line may be used:
| In[5]:= |
| Out[5]= |
A list of two lines may be used:
| In[6]:= |
| Out[6]= |
Find the intersection of two infinite lines:
| In[7]:= |
| Out[7]= |
Two lines in 3D:
| In[8]:= |
Find their intersection:
| In[9]:= |
| Out[9]= |
Show the lines and the intersection point:
| In[10]:= |
| Out[10]= | 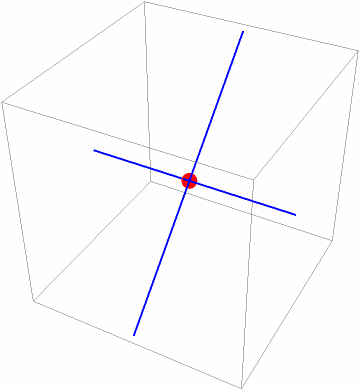 |
Ten thousand line pairs:
| In[11]:= |
Find the intersections and get timing:
| In[12]:= |
| Out[12]= |
In the documentation for InfiniteLine, the following method is used:
| In[13]:= | ![case1LineIntersection[{{a_, b_}, {c_, d_}}] := Module[{line1, line2},
line1 = InfiniteLine[{a, b}];
line2 = InfiniteLine[{c, d}];
{x, y} /. Solve[{x, y} \[Element] line1 \[And] {x, y} \[Element] line2, {x, y}][[1]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/7ff884e11299fb2e.png) |
That method is slower:
| In[14]:= |
| Out[14]= |
RegionIntersection may also be used:
| In[15]:= |
That method is also slower:
| In[16]:= |
| Out[16]= |
All three methods give the same results:
| In[17]:= |
| Out[17]= |
Inexact values may be used:
| In[18]:= | ![line1 = {{x, 2}, {5, 3}};
line2 = {{0, 1}, {1, a}};
ResourceFunction[
"LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/4f0fdccacb8a213d.png) |
| Out[20]= |
The lines are considered to be infinite lines, so the intersection point may not be on the defining segments:
| In[21]:= | ![line1 = {{3, 4}, {5, 3}};
line2 = {{0, 1}, {1, 0}};
p = ResourceFunction[
"LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/6bb2573c679bc2ff.png) |
| Out[23]= |
Show it:
| In[24]:= |
| Out[24]= |  |
Degenerate lines will not return an intersection point:
| In[25]:= | ![line1 = {{0, 0}, {0, 0}};
line2 = {{0, 1}, {1, 0}};
p = ResourceFunction[
"LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/020aa568077bf5a0.png) |
| Out[27]= |
Parallel lines will not return an intersection point:
| In[28]:= | ![line1 = {{-1, 0}, {0, -1}};
line2 = {{0, 1}, {1, 0}};
p = ResourceFunction[
"LineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][line1, line2]](https://www.wolframcloud.com/obj/resourcesystem/images/2a8/2a8d1d2c-e5b1-4fab-81eb-995e4ed924cb/18a0f148666b823e.png) |
| Out[30]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License