Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EulerEquations

Source Notebook

Get the Euler–Lagrange differential equations derived from a given functional

Contributed by: Wolfram Research

ResourceFunction["EulerEquations"][f,u[x],x]

returns the Euler–Lagrange differential equation obeyed by u[x] derived from the functional f, where f depends on the function u[x] and its derivatives, as well as the independent variable x.

ResourceFunction["EulerEquations"][f,u[x,y,…],{x,y,…}]

returns the Euler–Lagrange differential equation obeyed by u[x,y,…].

ResourceFunction["EulerEquations"][f,{u[x,y,…],v[x,y,…],…},{x,y,…}]

returns a list of Euler–Lagrange differential equations obeyed by u[x,y,…],v[x,y,…],….

Examples

Basic Examples (2) 

The Euler equations for the arc length in two dimensions yields a straight line:

In[1]:=
ResourceFunction["EulerEquations"][Sqrt[1 + y'[x]^2], y[x], x]
Out[1]=
In[2]:=
DSolve[%, y[x], x]
Out[2]=

A simple pendulum has the Lagrangian :

In[3]:=
ResourceFunction["EulerEquations"][ 1/2 m r^2 \[Theta]'[t]^2 + m g r Cos[\[Theta][t]], \[Theta][t], t]
Out[3]=

The solution to the pendulum equation can be expressed using the function JacobiAmplitude:

In[4]:=
DSolve[%, \[Theta][t], t]
Out[4]=

Scope (4) 

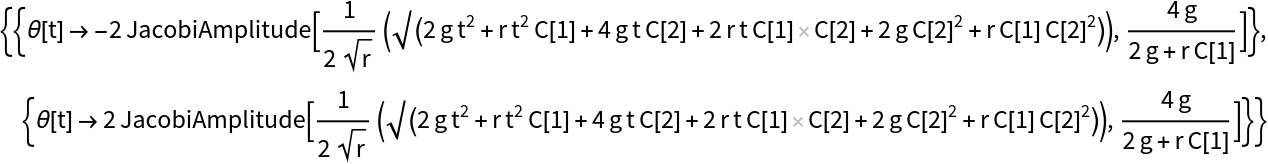The Lagrangian of a point particle in two dimensions has two dependent variables and yields Newton's equations:

In[5]:=
ResourceFunction["EulerEquations"][ 1/2 m (x'[t]^2 + y'[t]^2) - V[x[t], y[t]], {x[t], y[t]}, t]
Out[5]=

The Lagrangian of a point particle in two dimensions with a central potential:

In[6]:=
ResourceFunction["EulerEquations"][ 1/2 m (r'[t]^2 + r[t]^2 \[Theta]'[t]^2) - V[r[t]], {r[t], \[Theta][t]}, t]
Out[6]=

Second- and higher-order derivatives may be included in the integrand. A Lagrangian for motion on a spring using higher-order terms:

In[7]:=
ResourceFunction[ "EulerEquations"][-(1/2) m q[t] q''[t] - 1/2 k q[t]^2, q[t], t]
Out[7]=

The integrand has several independent variables:

In[8]:=
1/2 \!\( \*SubscriptBox[\(\[PartialD]\), \({{x, y, z}}\)]\(\[Phi][x, y, z]\)\) . \!\( \*SubscriptBox[\(\[PartialD]\), \({{x, y, z}}\)]\(\[Phi][x, y, z]\)\)
Out[8]=

The Euler equations yield Laplace's equation:

In[9]:=
ResourceFunction["EulerEquations"][%, \[Phi][x, y, z], {x, y, z}]
Out[9]=

Applications (3) 

The Euler equations for the integrand f[yxx,yx,y,x]:

In[10]:=
eqn1 = ResourceFunction["EulerEquations"][f[y''[x], y'[x], y[x], x], y[x], x]
Out[10]=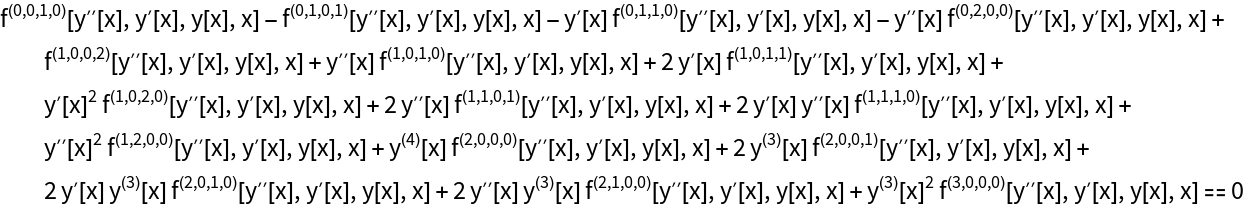

The "textbook" answer:

In[11]:=
eqns2 = D[Derivative[1, 0, 0, 0][f][y''[x], y'[x], y[x], x], x, x] - D[Derivative[0, 1, 0, 0][f][y''[x], y'[x], y[x], x], x] + Derivative[0, 0, 1, 0][f][y''[x], y'[x], y[x], x] == 0
Out[11]=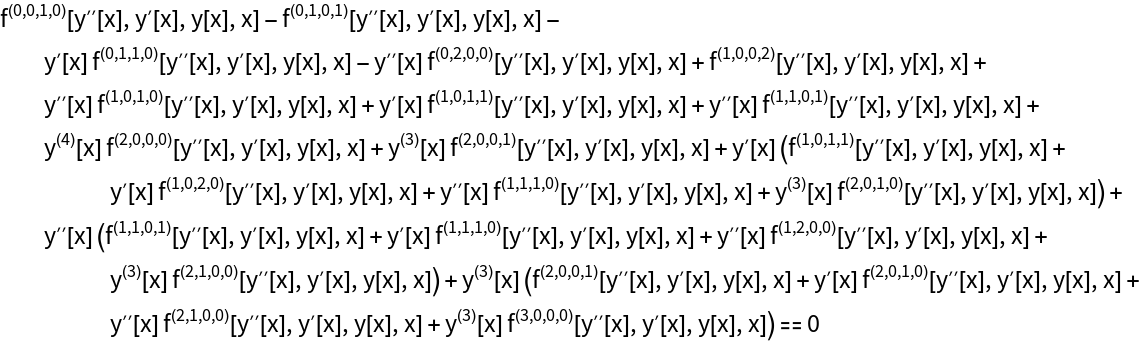

Check:

In[12]:=
eqn1 == Expand[eqns2]
Out[12]=

The brachistochrone problem asks for the curve of quickest descent. The time taken for a particle to fall an arc length ds is . If y measures the decrease in height from an initial point of release, then the velocity v satisfies:

In[13]:=
Solve[1/2 m v^2 == m g y, v]
Out[13]=

The equation for a curve joining two points, where a particle starting at rest from the higher point takes the least amount of time to reach the lower point:

In[14]:=
ResourceFunction["EulerEquations"][Sqrt[( x'[\[Theta]]^2 + y'[\[Theta]]^2)/( 2 g y[\[Theta]])], {x[\[Theta]], y[\[Theta]]}, \[Theta]]
Out[14]=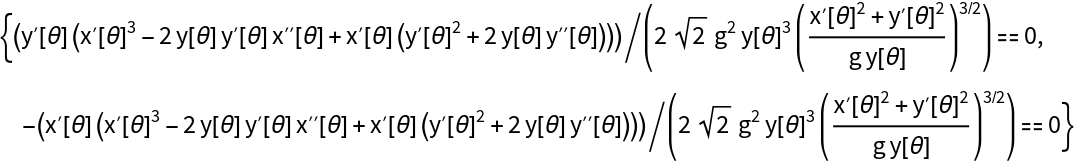

It is well known that the solution to the brachistochrone problem is a cycloid:

In[15]:=
% /. { x -> (k (# - Sin[#]) &), y -> (k (1 - Cos[#]) &) } // Simplify
Out[15]=

The Lagrangian for a vibrating string yields the classical wave equation:

In[16]:=
ResourceFunction["EulerEquations"][ 1/2 \[Rho] D[u[x, t], t]^2 - 1/2 \[Tau] D[u[x, t], x]^2, u[x, t], {x, t}]
Out[16]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 22 January 2019

Related Resources

License Information